国际金融市场波动非线性因果性和溢出效应①

夏南新

(中山大学岭南学院， 广州 510275)



国际金融市场波动非线性因果性和溢出效应①

夏南新

(中山大学岭南学院， 广州 510275)

摘要：针对人民币、欧元、日元兑美元的官方汇率，选取了2008年金融危机前后各三年的数据参照对比分析，计算三者汇率的均值方程的残差之间的交叉相关(cross-correlation function，CCF)，利用Yin-Wong Cheung, Lilian K. Ng检验统计量和Hong Y.检验统计量，验证3种汇率的标准残差的方差之间的非线性因果关系，并以此信息为依据构建BEKK-MGARCH模型，分析了人民币、欧元、日元兑美元的汇率的波动溢出效应，进而验证了各个变量序列方差之间非线性因果关系的稳健性.在Hong检验中引入了截断核函数，使得对低阶时滞项赋予了较大权重，从而准确地刻画近期波动对当前波动影响更大的特征.在建立Vector GARCH模型之前，很少有文献先进行方差的非线性因果关系检验，即使进行了简单检验，通常错误地把Q2(p)当作变量序列的方差之间的非线性因果关系检验统计量.

关键词：后金融危机时代； 汇率； 波动非线性因果性； 溢出效应

0引言

所谓后金融危机时代(post financial crisis era)，是指危机趋于缓和，虚拟经济逐渐从比重过大转为适中，世界经济仍然存在不稳定性，实体经济处于弱恢复期的时期.

2001年美国“9·11”事件发生后，全球经济增长更加乏力，世界主要经济体纷纷以降息方式刺激经济.美国实行低利率政策，投资者便大肆借贷美元，投资到利率较高的新兴市场以赚取利差.金融危机尤其是欧债危机爆发后，西方投资者不得不把资金撤离新兴市场，从而导致新兴经济体货币大幅贬值.

次贷危机爆发后，国际社会施行强度更大的刺激经济政策.美联储相继推出量化宽松货币政策(quantitative easing monetary policy).在第一轮量化宽松货币政策(QE1)执行期间(2008年11月25日至2010年4月28日)，美联储共购买了1.725万亿美元房利美(Fannie Mae)、房地美(Freddie Mac)等机构抵押贷款支持证券(mortgage-backed security)和机构债；2010年11月第二轮量化宽松货币政策启动，至2011年6月底以前以每月750亿美元的进度持续8个月，购买了总额约6 000亿美元的美国长期国债；2012年9月13日启动的第三轮量化宽松货币政策总额约6 000亿美元，将每月购买400亿美元机构抵押贷款担保债券，并视情况决定额外采购额度.接二连三的赤字货币化政策不仅无助于美国经济复苏，反而向市场注入了巨大流动性.发达经济体纷纷仿效美国，实施近零利率及量化宽松货币政策.大量短期资本在国际金融市场快速流动，加剧了粮食、能源等大宗商品价格飞涨，引发了全球性的输入性通货膨胀.英国、冰岛和爱尔兰等国的经济结构中金融比例偏高，首当其冲地受到影响.2011年，欧洲主权债务危机持续发酵，希腊等中东欧国家年财政赤字占GDP比率、公共债务占GDP比率，均远远高于欧盟《稳定与增长公约》所规定的3%和60%的上限.从2010年12月开始，全球3大评级机构惠誉、标准·普尔和穆迪纷纷调低希腊等国的主权信用评级，导致货币汇率大幅波动，欧元区银行业信贷危机一触即发，类似雷曼兄弟倒闭所引发的多米诺骨牌效应有可能再现.结构性危机后遗症正逐渐显现，经济恢复常态无时刻表.

二战后，世界建立了以布雷顿森林体系为基础的美元与黄金并重的国际金汇兑的双本位制货币体系，从而确立了美元在国际金融体系中的霸主地位.越战使得美国政府赤字高企，1971年尼克松政府宣布美元和黄金脱钩.1973年牙买加协议明确美元不与黄金挂钩，但各国货币仍与美元挂钩，至此维系近30年的布雷顿森林体系事实上宣告瓦解.1978年IMF成员国达成协议实行黄金非货币化，致使货币价值没有客观的衡量标准，货币的发行只能依靠国家信用，全球步入现代信用货币本位时代.

中国央行行长周小川则倡议，将国际货币基金组织的特别提款权(special drawing right， SDR)发展为超国家主权储备货币，并逐步替换现有储备货币即美元.不过，这些建议遭到了一些发达国家的抵制.

1文献综述

2011年10月11日，美国参议院通过了《2011年货币汇率监督改革法案》，该法案要求美国政府对“汇率被低估”的主要贸易伙伴征收惩罚性关税，显而易见，此项带有明显贸易保护主义色彩的法案旨在逼迫人民币加速升值.

李稻葵和尹兴中[1]认为国际金融危机之后，现行国际货币体系难以为继，尤其是因为美元信用基础发生了根本性的动摇，其超级国际货币的地位必然丧失；各国通力合作创造出超主权国际货币，欧元以及人民币不断崛起，与美元形成三足鼎立的多基准货币的新国际货币体系.朱民[2]认为这次金融危机宣布了以美元为中心的国际金汇兑本位制的国际货币体系的失败.吴治民和高宇[3]认为维持相对稳健的杠杆水平是中国金融业在危机中保持较好表现的根本原因.2009年以来，中国采取了以扩张资产负债表为特征的量化宽松货币政策，并辅以大规模扩张性财政政策，现正处于政策刺激性反弹向市场真实需求反弹的过渡阶段.目前，中国金融业处于高资本、消耗型、外延式增长发展模式，对资金的依赖性很大，过度地倚重于信贷的扩张.宋国才[4]指出国际货币体系多元化将成为趋势，人民币国际化带来了难得的发展契机，同时随着区域经济的不断加强，中国对于亚洲地区经济的影响力正在逐渐增强，人民币区域化流通的条件逐步形成.为此，中国将积极推进储备货币的多元化，加快签订货币互换协议，推进跨境贸易结算试点，而且逐步允许更大幅度的人民币可兑换，减少对资本跨境流动的控制，提供更多的以人民币计价的金融资产以供投资，让越来越多的国家和地区将人民币作为交易货币和外汇储备.

2011年3月11日日本东北部大地震后的两周时间内，日元非但没有贬值，反而小幅升值，而1995年1月17日日本阪神发生大地震后，日元同样出现升值.投资者普遍预期将会有大量海外资产被套现和赎回以满足日本灾后重建所需资金，于是，大举做多日元.不过，日本官方认为大地震后并未出现大规模的海外资金回流.日元与澳元套利交易的平仓操作，刺激了日元进一步升值.

郭珺和滕柏华[5]利用向量自回归模型和多变量GARCH模型，对人民币汇率改革以来人民币、欧元、美元和日元之间的收益溢出效应和波动溢出效应进行了研究，结果显示欧元、美元和日元对人民币存在显著的收益溢出效应和波动溢出效应. Kearney和Patton[6]分别建立了3、4、5个变量的欧洲货币体系中重要货币——法国法郎、德国马克、意大利里拉以及欧洲货币单位的汇率波动传导的多元GARCH模型；估计模型既没有对1979年4月至1997年3月的日数据也没有对周数据施加常数相关的共同限制；结果表明，检验多元GARCH模型设定稳健性是重要的，发现增加的短期综合项减少了观察波动性传递，并且马克通过波动传递起着支配地位.Bollerslev[7]基于多元GARCH模型分析了5种欧洲货币兑美元短期名义汇率的相干性，发现在欧洲货币体系中实行自由浮动汇率时期这5种欧洲货币之间存在较高显著的协同运动.McMillan等[8]基于欧元兑美元、英镑、日元的汇率，采用具有明显优势的Multi-GARCH现存的方差方法，检验这3种汇率是否存在波动溢出和时变相关性；检验结果表明，3种货币确实表现出一定程度的波动溢出和波动运动背后的驱动力的共性；考虑到相关系数中的时变性质，有大量证据表明相关性是随时间变化的，但在样本期相关系数值并没有增加.韩国高等[9]基于BEKK-MGARCH模型建立了中、美、日3国的实际均衡汇率方程和方差方程，对1994年以来中国、美国和日本的实际均衡汇率及其波动溢出效应进行了分析；结果表明，3个国家的实际均衡汇率受其经济基本面因素的影响不同，人民币实际均衡汇率还受到了美元和日元实际汇率的影响；中美、中日、美日之间的联动关系存在显著的ARCH和GARCH效应.

本文率先详尽地利用交叉相关(CCF)、Yin-Wong Cheung, Lilian K. Ng检验统计量和Hong Y.检验统计量，验证3个变量序列的标准残差的方差之间的非线性因果关系.经过各个变量序列的标准残差的方差之间非线性因果关系检验后，便构建BEKK-MGARCH模型，以验证各个变量序列方差之间的非线性因果关系的稳健性.在Hong检验中引入了截断核函数，使得对低阶时滞项赋予了较大权重，从而准确地刻画近期波动对当前波动影响更大的特征.

2非线性因果性检验引入

统计学上，波动溢出检验实质上是检验条件方差序列(二阶中心矩序列)之间是否存在Granger非线性因果关系.Cheung和Ng[10]采用一金融序列的均值方程生成的残差经标准化后的平方序列与另一金融序列的均值方程生成的残差经标准化后的平方序列之间的交叉相关函数(cross-correlation function，CCF)来检验方差(即波动)之间的非线性因果关系(即波动溢出)，其检验构想为

设信息集

(1)

其中Xt和Yt为平稳遍历时间序列.

假如

假如X与Y互为非线性因果，则X的方差与Y的方差之间会发生反馈效应.

如果

那么，存在方差的瞬时非线性因果性.

假定Xt与Yt可以写成

(2)

其中εt和ζt为0均值和单位方差的两个独立白噪声过程；hx,t和hy,t是基于t-1时刻信息集的条件协方差.

设Ut和Vt分别是标准新息εt和ζt的平方，有

(3)

Ut和Vt之间滞后k阶样本交叉相关为

(4)

其中cuv(k)是第k阶滞后或领先的样本交叉协方差，它由下式得到

(5)

其中cuu(0)和cvv(0)分别是U和V的样本方差.注意：不像自相关，交叉相关不必围绕0阶对称.

Hannan[11]指出，因为Ut和Vt独立，当样本容量趋向无穷大时，它们的二阶矩的扩展意味着

(6)

(7)

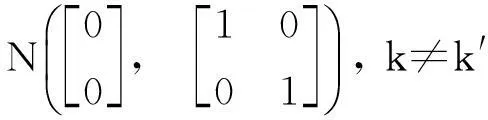
(8)

其中T为样本容量.

标准化残差平方的CCF可以用来探测和辨别二阶矩的非线性因果模式.

H0：CCF(k)=0(无非线性因果关系)

Ha：CCF(k)≠0(有非线性因果关系)

CCF方法不涉及到在序列内和在序列间动态(both intra and inter-series dynamics)的同期模型.当研究的序列数大并预期到非线性因果模式的长滞后时，CCF检验特别有用.CCF没有被设计探测产生0交叉相关的非线性因果模式.样本残差交叉相关进一步提供了有关时间序列数据间交互作用的信息.

(9)

它是有一个自由度(k-j+1)的卡方分布，即χ2(k-j+1)，能够用来检验从滞后j阶到滞后k阶没有非线性因果性的假设.当没有关于非线性因果性方向(Xt是Yt的原因，或者Yt是Xt的原因)的先验信息时，可以设置-j=k=m.参数m应该足够大到包括在非线性因果模式中可能出现的最大非0阶.当考虑一个非方向的因果性模式，即，Yt不是Xt的原因，设j=1和k=m.

当样本规模T小时，卡方统计量S可以被修正为

(10)

由于Cheung和Ng[10]的二阶矩非线性因果性检验、Granger[12]的一阶矩线性因果性检验给每一个滞后项均等权重，所以可以把它看作均匀加权，不过，非均匀加权常常比均匀加权给出了更好的检验功效(势)(power).鉴于此，Hong[13]提出了一类展示条件异方差和可能有无穷无条件方差的两序列之间波动溢出渐进标准正态检验.这种检验是基于两标准残差平方之间样本交叉相关平方加权和.允许使用所有样本交叉相关，并且介绍了每一滞后的样本交叉相关的柔韧性加权方案.基于Cheung和Ng统计量的广义版的Hong检验为

(11)

其中M是正整数，由于i(>M)阶的滞后项被赋予零权数，所以，M为滞后的截断数；k(·)是加权函数，可以是截断(truncated)核函数、巴特莱特(Bartlett)核函数、二次方程式谱(quadratic-spectral, QS)核函数，等等.

(12)

可见，Hong检验引入核权函数对低阶时滞项赋予较大权重，刻画近期波动比远期波动对当前波动影响更大的特征，样本交叉相关系数M随着样本规模T的增大而增大，即可以使用所有的滞后信息，从而确保在较大滞后阶数下仍然保持较强的检验功效(power).

3人民币、欧元、日元兑美元的汇率

的方差非线性因果性检验

第12任世界银行行长罗伯特·佐利克(任期2007年7月1日-2012年6月30日)认为，应恢复美元、欧元、英镑、日元以及人民币等众多货币与黄金挂钩的金本位制，以取代目前的美元体制.为此，本文特此选取了当今具有代表性货币的汇率，人民币、欧元、日元兑换美元的汇率，来考察后金融危机时代国际金融市场波动传导特征.

自2005年7月21日开始，中国汇率将以市场供求为导向，参考一篮子货币汇率的加权平均价作为人民币的基准汇率，中国人民银行还将根据市场发育状况适时调整汇率上下0.3%的浮动区间，以维持人民币汇率在合理和均衡水平上，进而促进国际收支的基本平衡.为此，人民币兑换美元官方汇率(CER)、欧元兑换美元官方汇率(EER)、日元兑换美元官方汇率(JER)的日数据时间跨度为2005年7月21日至2011年12月23日.这些数据均源自美国联邦储备网站(http://www.federalreserve.gov/Economic Research and Data).因各国法定节假日不同，为了使得3种汇率时间对齐，于是，没有交易的节假日缺失数据均采用线性插值法估测.每种汇率都有1 677个数据.样本期的中间刚好为2008年国际金融危机爆发时间，2008年前三年为金融危机滋长期，后三年为后金融危机时代，属于经济弱恢复期.以yt=(ycny,t,yeur,t,yjpy,t)T表示3个汇率的日收益率，其中

(13)

这3种汇率的日收益率的MultivariateGARCH模型中的均值方程是个常数项的回归方程(Hong[13]；高铁梅[15]；张世英和樊智[16])，其形式为

(14)

式中，εt=(ε1t,ε2t,ε3t)′服从均值为0，方差为Ht的条件正态分布.

人民币、欧元、日元兑美元的汇率序列取对数的均值方程如表1.

表1　人民币兑美元、欧元兑美元、日元兑美元的汇率均值方程

注： 1.圆括号内的数字为标准误，方括号内的数字为z统计量的值.

2.由于本文是研究异方差问题，均值方程生成的残差必须存在序列相关，所以，没有指出常数项的显著性以及R2值.

经检验，人民币兑美元汇率、日元兑美元汇率的均值方程的残差序列偏度小于0，表明序列左偏分布，而峰度都大于3，表明两序列呈尖峰分布；欧元兑美元汇率的均值方程的残差序列偏度大于0，表明序列右偏分布，而峰度也大于3，表明序列也呈尖峰分布.在零假设序列服从正态分布下，JB统计量服从χ2(2)，而1%显著性水平上临界值χ2(2)为9.210，这个序列的JB都远远大于它，同时p值也充分显示该统计量的显著性，由此可知，应该拒绝原假设，这进一步证实这3个汇率序列不服从正态分布(表2).

从图1、图2和图3中也可以直观看出.

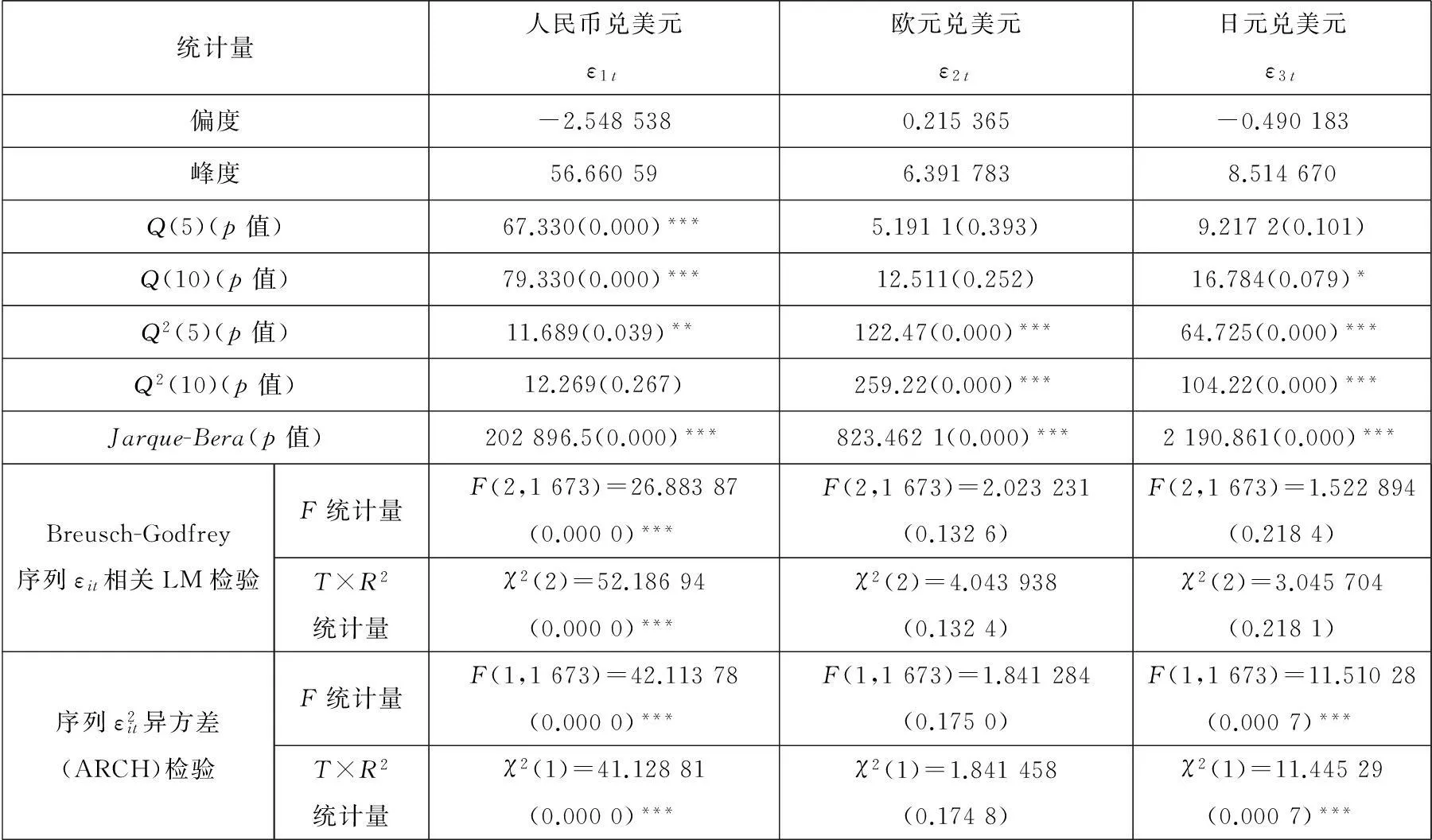
表2　人民币、欧元、日元兑美元汇率的均值方程的残差序列

注： 1.*、**和***分别表示在10%、5%和1%的显著性水平上拒绝零假设.

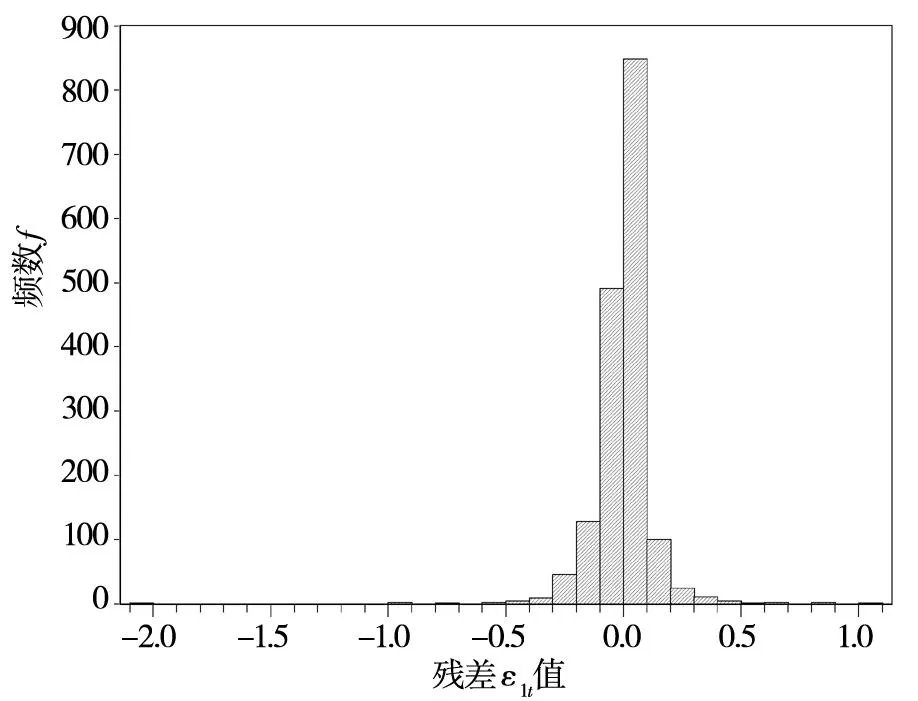
图1人民币兑美元的均值方程的残差序列直方图

Fig. 1 Histogram of residual sequence of the mean

equation of RMB against the U.S. dollar

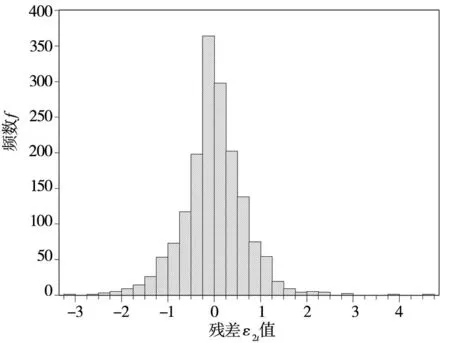
图2　欧元兑美元的均值方程的残差序列直方图

Breusch-Godfrey序列εit相关LM检验表明：人民币兑美元汇率的均值方程的残差序列相关LM检验的p值小于1%，该序列在1%的显著性水平上存在异方差，而欧元兑美元汇率的均值方程的残差序列和日元兑美元汇率的均值方程的残差序列不是很显著地存在异方差.

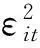
从图4、图5和图6中也可以直观看出.

图3　日元兑美元的均值方程的残差序列直方图

图4　人民币兑美元的均值方程的残差序列折线图

图5　欧元兑美元的均值方程的残差序列折线图

图6　日元兑美元的均值方程的残差序列折线图

人民币、欧元、日元兑美元汇率的均值方程的残差序列标准化后的平方的交叉相关见表3.

表3　人民币、欧元、日元兑美元汇率的均值方程的残差序列标准化后的平方的交叉相关

注：1.*、**和***分别表示在10%、5%和1%的显著性水平上显著，拒绝零假设.

3.k是期数.

4．交叉相关是渐进一致近似.

采用Hong检验统计量

使用截断核函数

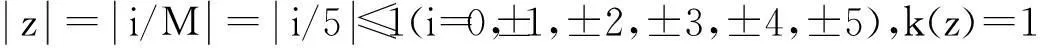
因果性检验其实就是一序列领先于另一序列的检验.从表4可以看出，Veur领先于Vjpy和Vjpy领先于Veur都是显著的，换句话说，Veur和Vjpy互为非线性因果关系显著，而Ucny与Veur、Vjpy之间互为非线性因果关系相对偏弱.人民币、欧元、日元兑换美元的标准新息的方差Ucny、Veur、Vjpy反映汇率波动程度，它们都是测定风险的指标.以上检验显示：欧元和日元波动的相互因果关系较强，人民币和欧元、日元之间的波动因果关系相对较弱.

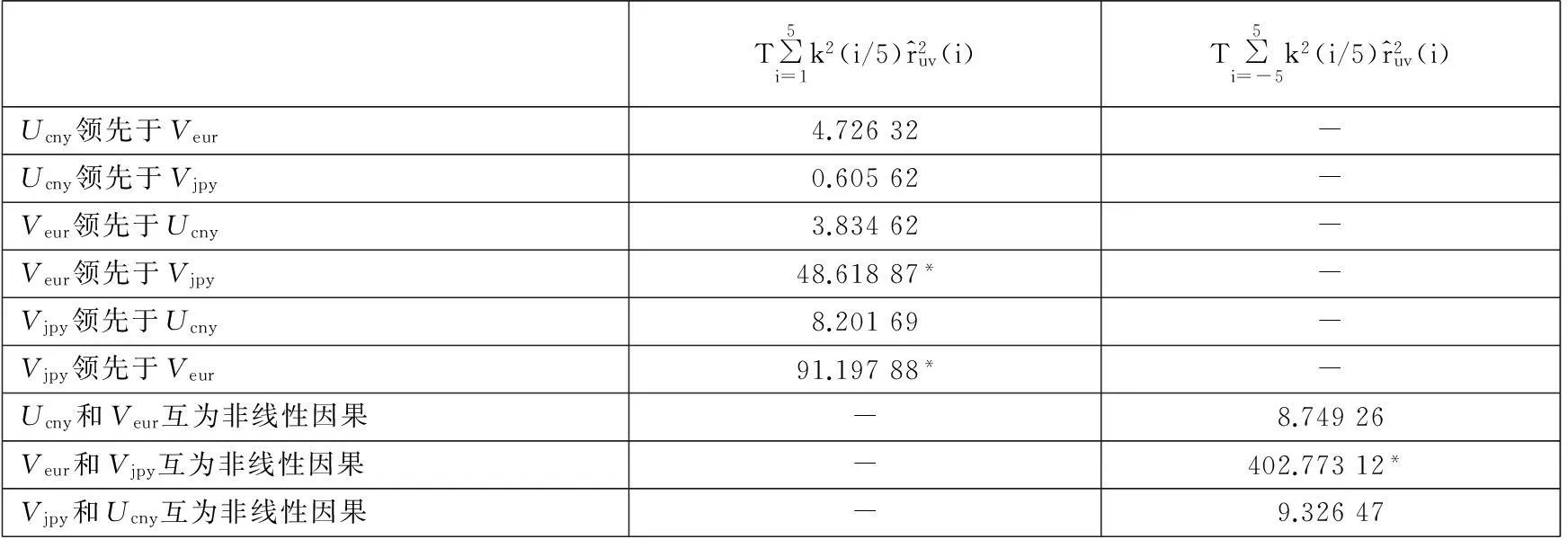
表4　人民币、欧元、日元兑美元汇率波动的非线性因果性检验

注：1.*、**和***分别表示在10%、5%和1%的显著性水平上显著.

3.Ucny、Veur、Vjpy分别表示人民币、欧元、日元的标准新息的方差.

4BEKK-MGARCH模型的引入

经过以上非线性因果性检验，便可以构建BEKK-MGARCH模型，从而验证各个变量序列的标准残差的方差之间非线性因果关系的稳健性.

由yt=(y1t,y2t,…,yNt)′的N因素的时变均值、方差、协方差的动态模型为

(15)

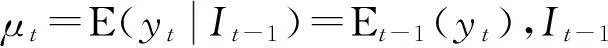
Bollerslev等[17]定义VEC(1,1)为

ht=c+Aηt-1+Ght-1

(16)

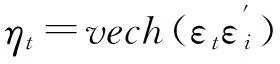
vech是把N×N下三角矩阵堆栈(stack)成为N(N+1)/2×1(注：N+(N-1)+(N-2)+…+2+1=N(N+1)/2)向量的算子

vechHt=(h11t,h21t,h22t,h31t,…,hNNt)′

(17)

vec是把一个矩阵堆栈成为一个列向量的算子

vec Ht=(h11t,h21t,…,hN1t,h12t,h22t,…,hNNt)′

(18)

在VEC(1,1)案例中，Ht的一般矩阵(不是vech)表达式为

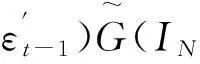
(19)

Engle和Kroner[18]在综合Baba等(1991年未发表手稿)的工作基础上提出以4人名字的第一字母命名的BEKK-GARCH模型.BEKK模型的优点在于它容易满足矩阵Ht的正定性，并且相对于向量GARCH模型，它具有相对较少的模型参数，不过，BEKK模型中的参数的经济涵义不如向量GARCH模型直观.

BEKK(1,1,K)模型定义为

(20)

5人民币、欧元、日元兑美元汇率的

收益率波动溢出效应分析

金融市场间汇率收益率序列一阶矩之间的动态联系和二阶矩之间的相互影响，均可以反映其波动传导机制.张世英和樊智[16]研究表明金融市场之间通过1阶的波动相关性能够解释金融时间序列的相关性.于是，人民币、欧元、日元兑美元汇率收益率波动模型设为BEKK-GARCH(1,1).具体形式为

(21)

其中方差-协方差Ht设定为对角(diagonal)BEKK；C是不确定矩阵；A1、G1是对角矩阵.

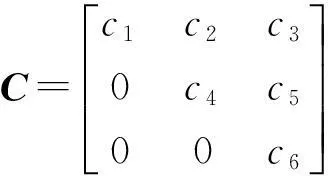
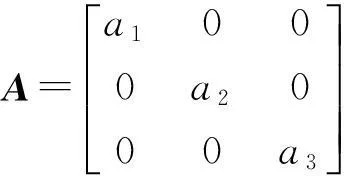
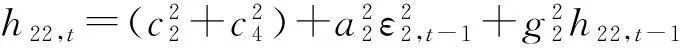
h12,t=c1c2+a1a2ε1,t-1ε2,t-1+g1g2h12,t-1，

h13,t=c1c3+a1a3ε1,t-1ε3,t-1+g1g3h13,t-1，

h23,t=(c2c3+c4c5)+a2a3ε2,t-1ε3,t-1+

g2g3h23,t-1

其中i，j=1(人民币)、2(欧元)、3(日元)；hii,t表示条件方差；hij,t表示条件协方差.aiaj反映汇率波动的ARCH效应对当期汇率波动或协同变动的影响程度；gigj反映汇率波动的GARCH效应对当期汇率波动或协同变动的影响程度.

由于对角multivariate GARCH模型简化了多个变量之间的相关关系，因而无法通过对角向量GARCH模型来研究多个市场波动之间的相互关系和溢出效应.韩国高等[9]指出，由于联立求解方程，实际上在反映两个市场间的波动相关性时，已经间接考虑了其它市场的影响，而且比较容易考察两两市场之间的波动相关程度.

采用ARCH极大似然(marquardt)估计方法对BEKK-GARCH(1,1)进行拟合，具体结果如表5.

表5　人民币兑美元、日元兑美元、欧元兑美元的汇率BEEK(1,1)-GARCH

注： 1.*、**和***分别表示在10%、5%和1%的显著性水平上拒绝零假设.

2.假设残差服从正态分布，通过观察方程的约束式和非约束式的对数似然估计值的差异来进行似然比检验.通过连续增加变量滞后期数k，直到SC或AIC取得极小值，从而确定最优滞后期k，换而言之，SC和AIC的值越小越好.其中，SC=-2(lnL/T)+klnT/T；AIC=-2(lnL/T)+2k/T；极大似然函数lnL=-(T/2)[1+ln(2π)+ln(ε′ε/T)]；ε′ε是残差平方和的向量形式；T为样本容量；k为模型中变量的最大滞后期.

在条件方差方程中，上一期残差平方项与上一期条件方差项的系数之和分别为

a22+g22=0.999 297,

a33+g33=0.994 748

在条件协方差方程中，上一期残差对应相乘项与上一期条件协方差项的系数之和分别为

a12+g12=0.974 014，

a13+g13=0.960 666，

a23+g23=0.996 714

都接近1，这表明人民币、欧元、日元兑美元汇率收益率波动的相互传递影响h12,t、h13,t、h23,t具有持续性，彼此之间都有波动溢出效应.前两数字不如后一数字更接近1，可见，人民币和欧元之间、人民币和日元之间的波动传递影响持久性相对较弱，而欧元和日元之间的波动传递影响持久性相对较强，这与前面的因果性检验相吻合.

6结束语

以上实证分析表明：由于当前我国实行有管理的浮动汇率制度，人民币外汇市场尚不成熟，所以，人民币与欧元或日元的波动相互影响较弱.由此可见，在后金融危机时代，国际金融市场波动在一定程度上正呈现出趋同性.

互联网技术加速了国际金融市场的交易信息扩散，使得国际金融市场联系更加紧密，影响更加深刻，一体化趋势更加迅速.随着人民币汇率形成机制改革的深化，人民币汇率的市场化，人民币正在逐步融入世界主要货币市场，与此同时，人民币必然要面临着其他货币波动的冲击，加剧人民币波动风险.

20世纪30年代世界经济大萧条，1929年股票市场大崩盘之后，人们普遍认为经济危机已经结束，可是经济危机于1931年5月却再度发生，从而致使世界经济步入10年萧条期.2008年金融危机爆发后不久，有业界人士认为金融危机即将过去，但是，2010年欧债危机却突然袭来.2011年8月5日，标准·普尔将维持了近百年的美国长期主权信用评级AAA贬为AA+，穆迪与惠誉对其负面展望.在后金融危机时代，人民币汇率自由浮动的条件尚不成熟，易受到国际金融市场欧元、日元等主要货币汇率波动风险的传导冲击，而人民币对世界主要货币的影响力却相对较弱.冲击与反冲击的不对称性，影响的单向性，迫切需要加快培育人民币汇率市场，扩大人民币汇率浮动区间，以增加人民币汇率的弹性，提升人民币国际化程度.汇率政策制定者和汇率市场参与者应该密切关注国际汇率市场的变化，建立风险预警机制和风险管控措施，化解人民币汇率的外来风险.

自2005年7月21日至2011年12月23日，美元总体上处于贬值过程，而人民币、欧元、日元相对于美元均表现为升值，其中，人民币升值幅度为30.62%，欧元升值幅度为7.65%，日元升值幅度为41.39%.以超强货币美元为参照，分析人民币、欧元、日元兑换美元的汇率的波动引起的彼此之间的冲击与反冲击，从而使得冲击与反冲击强度具有可比性.

2005年7月人民币汇改提及到的一篮子货币，其选取货币及其赋予的权重主要取决于外币相应国家与中国贸易额、外债规模、投资等，而在这些方面美国都具有绝对优势，因而在一篮子货币中美元自然占大比重，人民币实际上仍然挂钩美元.在中国外汇储备中，美元资产占比约65%，欧元资产占比约25%，日元资产占比约3%.可见，我国储备资产的价值易受到美元贬值风险的影响，中国外汇储备币种结构和资产结构亟待优化，以实现外汇储备资产多元化战略.尽管日元正处于贬值期，但是，日元还是存在反转升值的潜力，可以适当减持美元计价资产，逢低价时机可以适当增加日元等非美元计价资产，以获得今后日元等货币升值的收益.虽然建立在蒙代尔最优货币区理论基础上的欧元相对美元总体上处于小幅升势，但是，自2010年初以来，欧元区忙于应对债务危机，经济停滞，正面临着主权债务风险.由于日元汇率和欧元汇率波动的风险相互传导十分显著，因此，欧元资产难以对冲日元资产风险，与此同时增持欧元资产须谨慎.2010年6月，中国央行宣布重启人民币汇改，强调人民币汇率参考一篮子货币进行调节，旨在真正意义上形成一篮子货币机制.

日元作为避险货币时常走高，日元兑美元汇率持续窄幅盘整.为了遏制外汇市场投机行为，2011年日本政府3次干预汇市.日本遭受“3·11”大地震及其核泄漏重创后，大批企业移居海外，造成日本产业空心化.2011年8月24日，穆迪宣布将日本政府债券评级下调一级，降至Aa3，标准·普尔与惠誉也将日本主权信用评级展望调至负面.日本人均债务额已高达747万日元.为此，应当密切防范日本主权债务风险对我国外汇储备资产的影响.

2011年11月30日至12月12日，人民币兑美元连续9个交易日出现盘中触及跌停点的情况，这是汇改以来的首次.国际投机资本做空新兴经济体，外汇市场上释放出人民币汇率技术性贬值信号，有望改变人民币持续近7年的单边升值趋势，表明人民币汇率逐渐趋近均衡汇率水平.尽管此次人民币汇率只是技术性回调，尚未形成趋势性贬值预期，但是，可以暂时舒缓人民币单边升值预期压力，展现出人民币汇率有升有降的天然弹性.

优化全球经济治理结构，加快国际货币体系改革进程，建立超主权的国际货币，增强经济体权利与义务的对称性.掌控人民币汇改节奏，完善人民币汇率形成机制，推进人民币国际化，以提升人民币汇率应对美元、欧元、日元等世界主要货币汇率波动冲击与反冲击能力.借助人民币升值契机，加快对海外企业并购和大宗商品购买，使人民币升值的益处可视化.

参 考 文 献：

[1]李稻葵， 尹兴中. 国际货币体系新架构： 后金融危机时代的研究[J]. 金融研究, 2010, 356(2): 31-43.

Li Daokui, Yin Xingzhong. The international monetary system in the era of post-financial crisis: What policy options does China have?[J]. Journal of Financial Research, 2010, 356(2): 31-43.(in Chinese)

[2]朱民. 研究“危机后的世界经济金融格局”的五个问题[J]. 国际经济评论, 2009, 82(7/8): 25-27.

Zhu Min. Five issues of "world’s economic and financial structure in the post-crisis era"[J]. International Economic Review, 2009, 82(7/8): 25-27. (in Chinese)

[3]吴治民, 高宇. 后危机时代中国金融监管理念变革与政策调整[J]. 财经科学, 2010, 27, (211): 1-8.

Wu Zhimin, Gao Yu. Study on the principle innovation and policy adjustment of financial regulation in China in post-crisis era[J]. Finance and Economics, 2010, 27(211): 1-8. (in Chinese)

[4]宋国才. 后危机时代中国金融市场发展分析[J]. 经济视角, 2011, 203(6): 100.

Song Guocai. Analysis on the development of financial market in China in post-crisis era[J]. Economic Vision, 2011, 203(6): 100. (in Chinese)

[5]郭珺, 滕柏华. 人民币与欧元、美元、日元之间的汇率联动分析[J]. 经济问题, 2011, 383(7): 95-104.

Guo Jun, Teng Baihua. Dynamic linkage analysis to the exchange rates of RMB, the Euro, the Dollar and the Yen[J]. On Economic Problems, 2011, 383(7): 95-104. (in Chinese)

[6]Kearney C, Patton A J. Multivariate GARCH modeling of exchange rate volatility transmission in the European monetary system[J]. The Financial Review, 2000, 35(1): 29-48.

[7]Bollerslev T. Modeling the coherence in short-run nominal exchange rates: A multivariate generalized arch model[J]. The Review of Economics and Statistics, 1990, 72(3): 498-505.

[8]McMillan D G, Ruiz I, Speight A. Correlations and spillovers among three Euro rates: Evidence using realised variance[J]. The European Journal of Finance, 2010, 16(8): 753-767.

[9]韩国高, 陈喻喆, 高铁梅. 中、美、日实际均衡汇率模型的构建及实证研究[J]. 数量经济技术经济研究, 2011, 28(1): 76-88.

Han Guogao, Chen Yuzhe, Gao Tiemei. Real equilibrium exchange rate model of China, U.S. and Japan[J]. The Journal of Quantitative & Technical Economics, 2011, 28(1): 76-88. (in Chinese)

[10]Cheung Y-W, Ng L K. Causality-in-variance test and its application to financial market prices[J]. Journal of Econometrics, 1996, 72(1/2): 33-48.

[11]Hannan E J. Multiple Time Series[M]. New York: John Wiley, 1970: 536-536.

[12]Granger C W J. Investigating causal relations by econometric models and cross-spectral methods[J]. Econometrica, 1969, 37(3): 424-438.

[13]Hong Y M. A test for volatility spillover with application to exchange rates[J]. Journal of Econometrics, 2001, 103(1/2): 183-224.

[14]Priestley M B. Spectral Analysis and Time Series, Vol.1[M]. London: Academic Press, 1981.

[15]高铁梅. 计量经济分析方法与建模[M]. 北京: 清华大学出版社, 2009: 431.

Gao Tiemei. Econometric Analysis Method and Modeling[M]. Beijing: Tsinghua University Press, 2009: 431. (in Chinese)

[16]张世英, 樊智. 协整理论与波动模型: 金融时间序列分析及应用[M]. 北京: 清华大学出版社, 2004: 292.

Zhang Shiying, Fan Zhi. Co-integration Theory and Fluctuation Model: Financial Time Series Analysis and Application[M]. Beijing: Tsinghua University Press, 2004: 292. (in Chinese)

[17]Bollerslev T, Engle R F, Wooldridge J M. A capital asset pricing model with time-varying covariances[J]. Journal of Political Economy, 1988, 96(1): 116-131．

[18]Engle R F, Kroner K F. Multivariate simultaneous generalized arch[J]. Econometric Theory, 1995, 11(1): 122-150.

Nonlinear causality and spillover effect of volatility of international finance market

XIANan-xin

Lingnan College, Sun Yat-sen University, Guangzhou 510275, China

Abstract:By computing the residual cross-correlation function (CCF),this paper attempts to explore the nonlinear causality and spillover effect of volatility of the series of the official exchange rates of China, Europe and Japan, respectively, against the USA dollar by employing daily data from Jul. 21, 2005 to Dec. 23, 2011. Test statistics of nonlinear causality of conditional variance developed by Yin-Wong Cheung, Lilian K. Ng and Hong Y. are used to examine the nonlinear causal relationship between the variances of standardization residual of the three kinds of exchange rates. There upon, a BEKK-MGARCH model is built. Finally, the nonlinear causality and spillover effect of volatility on these exchange rates in post financial crisis era are analyzed and interpreted, and the robustness of the nonlinear causal relationship between the variances of time series is verified. The embedding of the truncated kernel function in Hong test causes the low order lag terms a given greater weight, thereby accurately portrays the characteristics that recent fluctuations have a larger impact on current fluctuations. Prior to the establishment of the Vector GARCH model, few literatures tested the nonlinear causal relationship first, even though some conducted a simple test, they mistakenly treated Q2(p) as the test statistic of the nonlinear causal relationship between the variances of variable sequences.

Key words:post financial crisis era; exchange rate; nonlinear fluctuation causality; spillover effect

中图分类号:F8

文献标识码:A

文章编号:1007-9807(2016)03-0064-13

作者简介:夏南新(1961—)， 男， 江西南昌人， 博士， 教授, 博士后导师. Email: xianx@mail.sysu.edu.cn

基金项目：国家社会科学基金重点资助项目(15AJL005)； 国家社会科学基金重大资助项目(12ZDA020).

收稿日期：(①) 2013-05-26；

修订日期：2014-02-22.