基于LASSO分位数回归的对冲基金投资策略研究①

蒋翠侠， 刘玉叶， 许启发

(1. 合肥工业大学管理学院， 合肥 230009；2. 合肥工业大学过程优化与智能决策教育部重点实验室， 合肥 230009)



基于LASSO分位数回归的对冲基金投资策略研究①

蒋翠侠1, 2， 刘玉叶1， 许启发1, 2

(1. 合肥工业大学管理学院， 合肥 230009；2. 合肥工业大学过程优化与智能决策教育部重点实验室， 合肥 230009)

摘要：由于对冲基金采用了灵活的投资技巧，其收益序列往往表现出与传统投资方式不同的统计特征与风险收益能力，已有方法难以有效地评价其投资绩效.基于LASSO分位数回归，从影响对冲基金收益的众多风险因子中，挑选出重要的风险因子，考察在不同分位点处对冲基金的收益与风险之间关系，识别对冲基金投资风格，继而给出对冲基金投资绩效评价方法.为验证基于LASSO分位数回归的投资风格识别与投资绩效评价效果，构建对冲基金风格组合投资方案，并将其与基于均值回归构建的组合投资、等权组合投资、Markowitz组合投资等经典的组合投资决策方法进行比较.实证研究结果表明，基于LASSO分位数回归的投资绩效评价方法最为有效，给出的组合投资方案能够获得较高的风险调整收益.

关键词：对冲基金； LASSO分位数回归； 对冲基金绩效； 风格组合投资

0引言

近年来，对冲基金规模迅速扩大，对冲基金凭借对冲、卖空、贷杠、套利等灵活的投资技巧和多样化的投资策略，在证券市场上赚取高额回报，受到越来越多投资者的关注.如何识别对冲基金投资风格与评价对冲基金投资绩效，关乎广大机构投资者与个人投资者的利益，影响到金融市场的繁荣与稳定.过去，主要使用均值回归分析方法对此开展研究，一方面，通过回归系数的显著性，探寻不同的风险因子对对冲基金收益的影响，识别对冲基金投资风格；另一方面，通过回归模型的截距项：Jensen的α指数，评价对冲基金投资绩效.由于对冲基金投资的高度动态性和基金经理操作透明度的缺乏，如何识别出包含在模型中最重要的风险因子仍然非常困难，这涉及统计分析中的变量选择问题.关于变量选择，线性回归模型的逐步回归方法为此提供了较好的手段，往往可以识别出重要的风险因子而广泛应用于对冲基金的定量研究.然而，由于对冲基金投资策略不同于传统的投资方式，其收益序列也往往表现出不同的统计特征和风险收益能力，如：Fung等[1]的研究发现，对冲基金收益往往具有更加严重的肥尾、有偏、高峰等典型特征.许启发等[2]指出，当响应变量服从非对称分布或散布较大时，均值回归很难具有代表性.因此，建立在均值回归基础上的对冲基金风格分析与绩效评价方法面临巨大挑战，需要开发新的工具与方法，准确揭示各个风险因子对对冲基金收益整个分布特征(不局限于均值)的影响.

与均值回归不同，Koenker等[3]提出的分位数回归，能够细致地刻画解释变量对响应变量整个条件分布的影响.该分析方法已被广泛应用于金融经济、环境科学、公共卫生等学科领域，详见Yu等[4]的文献综述.分位数回归分析已成功应用于基金管理研究，代表性工作有：Bassett等[5]使用线性分位数回归对共同基金投资风格进行定量研究；Meligkotsidou等[6]使用贝叶斯分位数回归评价了对冲基金投资绩效.这些良好实证效果的取得，主要得益于分位数回归不仅能够像均值回归一样可以揭示风险因子对于对冲基金平均收益的影响，而且能够刻画在较高和较低分位点处各个风险因子对对冲基金收益的影响，这为揭示对冲基金极端收益变动规律奠定了基础.不过，在使用分位数回归分析进行重要风险因子识别过程中，也涉及变量选择问题.Meligkotsidou等[6]使用信息准则：AIC与BIC对此进行选择，需要估计2K(K为解释变量的数目)个模型并计算其AIC、BIC值，工作量巨大.在高维数据分析领域，Tibshirani[7]提出的LASSO(least absolute shrinkage and selection operator)方法主要通过将一些不重要的变量缩减为0，从而能够一次完成变量选择与参数估计，极大地减小了计算量，快速实现变量选择过程.LASSO方法已被广泛应用于均值回归模型，较好地实现了变量选择，详见李根等[8]的文献综述.该方法也被成功应用于分位数回归分析中的变量选择，得到LASSO分位数回归模型.这一研究工作最早可以追溯到Koenker等[9]，他们使用的总变化平滑惩罚，可以被视为L1惩罚.Wang[10]将最小绝对偏差LAD方法与LASSO方法即L1惩罚函数相结合，得到了稳健的分位数(中位数)回归模型；李熠熠等[11]利用该方法对利率期限结构进行了实证研究；Li等[12]、Lamarche[13]、Belloni等[14]、李翰芳等[15]分别使用了LASSO方法讨论了分位数回归的高维变量选择问题.

迄今，尚无文献将LASSO分位数回归应用于对冲基金投资策略研究，本文拟就此开展研究工作.首先，基于LASSO分位数回归，判定对冲基金投资风格.LASSO分位数回归同时兼具LASSO的变量选择功能和分位数回归功能，一方面，通过变量选择，能识别出在不同分位点处重要的风险因子，另一方面，通过分位数回归，能够细致考虑在不同分位点处风险与收益关系.因此，LASSO分位数回归能够准确识别对冲基金投资风格.其次，基于LASSO分位数回归系数，构造风险调整的α*指数，以评价对冲基金投资绩效.不同于Jensen的α指数，这里的α*同时考虑了收益与风险两个方面，能够给出更加合理的评价结果.最后，基于LASSO分位数回归的投资绩效评价结果，构造风格组合投资，评估本文提出方法的有效性.实证比较了基于LASSO分位数回归的风格组合投资与经典的组合投资方法，结果显示前者的投资绩效评价方法较为可靠，给出的组合投资方案能够获得更高的风险调整收益.

1模型与方法

1.1对冲基金风格的均值回归分析

1.1.1均值回归模型构建

考虑对冲基金收益序列{rt}t=1,2,…,T以及用于解释其收益率的K个风险因子收益序列：{fi,t}i=1,2,…,K;t=1,2,…,T.为定量研究对冲基金收益的构成，可以使用多因子的资产定价模型，建立标准的线性均值回归模型

(1)

式中α为截距项；βi为回归系数；εt为随机扰动项.

1.1.2均值回归模型估计与变量选择

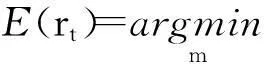
(2)

得到模型的参数估计结果与收益序列的条件期望.

当考虑的风险因子数目较多时，需要对其进行变量选择，可以采用逐步回归方法，包括向前逐步回归与向后逐步回归.该方法的核心思想在于通过F检验设置变量进入与退出的门槛，将那些贡献显著的风险因子保留在模型中，直到最后再没有显著贡献的风险因子可以引入，也没有不显著的风险因子需要退出时为止.最终，根据保留在模型中的风险因子类型(价值型，成长型和平衡型；大盘、中盘和小盘)识别对冲基金投资风格.

1.2对冲基金风格的分位数回归分析

1.2.1分位数回归模型构建

然而，条件均值回归模型只能揭示对冲基金的平均收益如何受风险因子的影响.由于对冲基金收益的特殊统计特征，平均收益已经很难具有代表性，或者说实际中对冲基金往往难以取得平均收益，更有可能取得一些极端收益.蒋翠侠等[17]建议，可以从条件密度建模或者条件分位数建模两个不同角度，来揭示响应变量整个条件分布变动规律.为此，本节使用分位数回归分析揭示对冲基金收益在不同尾部如何受到风险因子的影响，从而细致刻画对冲基金收益整个条件分布的动态性.建立线性分位数回归模型为

(3)

式中τ(0<τ<1)为分位点；α(τ)为截距项；β(τ)=(β1(τ),β2(τ),…,βK(τ))′为τ分位点处的回归系数向量，随分位点而变化，表现出异质性.

由模型(3)可以得出在给定K个风险因子的收益率f1t,…,fKt时，对冲基金收益rt第τ条件分位点的值为

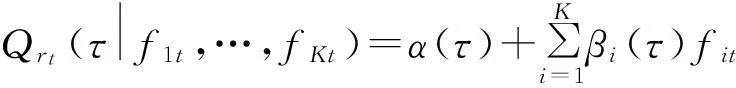
1.2.2分位数回归模型估计与变量选择

一般地，收益序列的第τ分位数，可以通过简单的优化问题来估计,即

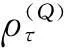
(4)

以得到模型的参数估计结果与收益序列的条件分位数.Portnoy等[18]将其转化为线性规划问题，并给出其求解的内点算法.

当考虑的风险因子数目较多时，也需要对其进行变量选择，这里使用LASSO分位数回归来实现.LASSO分位数回归主要通过在原分位数回归目标函数基础上，增加个L1惩罚项得到

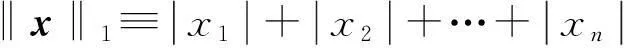
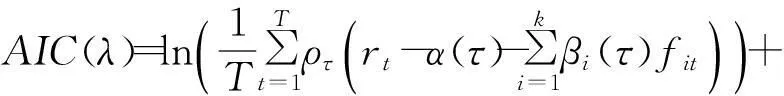
(6)

式中df为模型的有效维度.

对LASSO分位数回归模型进行求解，可以转化为对应的约束优化问题

(7)

式中s为与λ相对应的约束参数，s取值越小，将βi(τ)系数约束到0的作用越强.进而，可以使用Efron等[19]提出的LARS(leastangleregression)算法，对规划问题进行求解.与均值回归模型不同，LASSO分位数回归的结果使得最终保留在模型中的风险因子在不同分位点处可能会有所差异.这一现象表明，均值回归仅仅考虑风险因子对平均收益的影响，进而识别对冲基金投资风格，势必会带来偏差.需要通过LASSO分位数回归，细致地考察整个对冲基金收益分布状况，不仅能够挑选出对中间收益影响显著的风险因子，而且能够挑选出对不同尾部特征影响显著的重要风险因子，识别对冲基金投资风格.

1.3对冲基金风格组合投资选择方法

1.3.1单个对冲基金风格绩效评价

众所周知，对冲基金往往比传统的投资工具有更优越的绩效表现，这主要归功于对冲基金管理人的投资技能.对于对冲基金投资策略进行绩效评价，最常用Jensen的指数.该指数是均值回归模型中对冲基金收益超过市场指数解释部分的溢价，即均值回归模型中的截距项.然而，Amin等[20]指出，尽管Jensen的指数是个很好的绩效衡量工具，但关于它对于对冲基金评价的适用性仍存在一些争议.由于对冲基金管理人所采用的高动态复杂交易策略，对冲基金回报表现出一些特殊性，如更加严重的肥尾、有偏、高峰等特征.所以，基于正态性假设的条件均值回归方法和以相应的回归系数作为绩效衡量工具，并不适合模拟和评价对冲基金绩效.为了合理地评价对冲基金投资绩效，需要考虑对冲基金收益的整个条件分布.

为此，考虑基于LASSO分位数回归的α*指数，用于评价对冲基金投资绩效.α*指数定义为

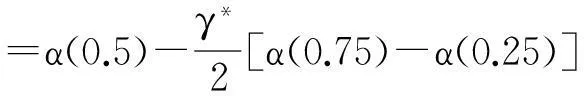
(8)

式中α(0.5)为LASSO分位数回归模型中截距项在中位点处的估计值，表示绩效的水平；α(0.75)和α(0.25)分别为75%分位点和25%分位点处的α估计值，[α(0.75)-α(0.25)]表示绩效的波动，可以视为风险；γ*代表风险厌恶参数，γ*越大，表示投资者风险厌恶程度越高.事实上，这里的α*指数为线性效用函数，在绩效水平与绩效风险之间进行权衡，α*越大，表明对冲基金投资绩效越好.

1.3.2组合对冲基金风格绩效评价

为进一步衡量本文提出的基于LASSO分位数回归的对冲基金投资绩效评价效果，在对冲基金投资绩效评价基础上，根据排序结果构建风格组合投资，并对组合投资效果进行评价.如果所得组合投资效果比其他方法所得组合投资效果好，则表明本文的方法是有效的.

对于构建的风格组合投资效果进行评价，可以使用风险调整后收益，最常用的是Sharp[21,22]提出的Sharp比率

(9)

式中E(rp)为组合投资的期望收益；σ为组合投资收益的标准差.Sharp比率可以解释为每单位风险的平均收益，陈收等[23]认为，当考虑在众多的基金中选择购买某一只基金时，Sharp比率可以作为一项重要的依据.然而，Sharp比率存在自身的局限性：第一，正态性假设使它不能很好地适用于对冲基金绩效评价；第二，使用标准差作为衡量风险的工具：将收益的上升与下降等同地视为风险.一般地，收益下降才视为风险，称为下行风险，定义为

(10)

式中RV是个参考值，代表投资者所能接受的最小回报或收益.在此基础上，Sortino等[24,25]提出了另外一种考虑风险调整的绩效衡量工具，Sortino比率，定义如下

(11)

式中δ为下行风险.对比Sharp比率与Sortino比率，主要区别在于：第一，后者增加了投资者能够接受的最低回报水平；第二，用下行风险替代了标准差风险.因此，Sortino比率更加接近实际，能够给出组合投资绩效的合理评价.

2实证研究

2.1数据与描述

根据对冲基金投资属性，国内对冲基金可以分为4大类，其中一级策略有相对价值型策略、方向型策略(包括管理期货策略、股票多空仓策略、固定收益方向型策略和宏观策略)、事件驱动型策略和基金的基金策略.迄今，共有7只对冲基金单一策略指数：相对价值指数(RV)、管理期货指数(MF)、股票多空仓指数(ES)、固定收益方向型指数(FI)、宏观策略指数(M)、事件驱动指数(ED)和基金的基金(FOF).考虑到中国在2010年3月底开始融资融券操作，设定样本区间为2010-04～2014-09，数据频率为月度数据，数据来源于阿尔法研究中心的对冲网数据库.上述样本区间中，2010-04～2013-10的样本数据为阿尔法研究中心编制的指数数据(10月以后策略指数编制工作停止)；2013-11～2014-09为本文整理计算结果.指数计算过程中，主要依据阿尔法研究中心提供的成份基金列表和指数编制规则，采用简单加权平均法，以成份基金的平均复权单位净值增长率作为指数增长率，从而得到计算期指数点位.本文所有计算均在R3.0.1软件下完成，感兴趣的读者可以来函索取相应代码.

为全面反映股票市场、债券市场收益情况以及对冲基金投资风格特征，回归因子主要选取Fama-French 3因子(市场溢酬因子RF、市值因子SMB和账面市值比因子HML)以及中信标普风格指数和债券指数，共计11个因子.首先，通过Fama-French 3因子表征股票市场收益，数据来自国泰安数据库.其次，通过风格因子表征对冲基金的投资风格.为避免信息重复，本文主要考虑了两个维度：投资风格、市场代表性，从中信标普开发的16只风格指数中选取6只风格指数.就投资风格而言，只有选择纯成长指数与纯价值指数这一组合，才能避免信息重复.不过，这一组合遗漏了一个平衡型投资风格，本文使用中信标普开发的债券指数(国债指数TB和企业债指数CB)作为替代.就市场代表性而言，100指数的成分股包括中国A股市场中市值最大、流动性最强的100只股票；200指数代表了中国A股各行业上市公司中自由流通市值最大、最具流动性并且财务稳健的300家公司中去除100指数成分股的所有中盘股票；而小盘指数则包含了除中信标普100和200以外的300只最具投资性的小市值股票.综合上述，两个维度交叉组合共形成了6只风格指数：100纯成长指数(OPG)、100纯价值指数(OPV)、200纯成长指数(TPG)、200纯价值指数(TPV)、小盘纯成长指数(SPG)和小盘纯价值指数(SPV).这6只风格指数，不仅揭示了不同投资风格，也体现了市场整体表现，具有很好的代表性.最后，通过债券指数表征债券市场收益.以上样本区间也为2010年4月到2014年9月，数据频率为月度数据，数据来源于中信标普指数服务下载中心.

表1给出了对冲基金收益率的描述性统计结果，可以看到，对冲基金策略指数的收益与标准差都存在较大差异，并且收益与标准差之间并非完全对应，与金融市场上投资回报之间的“高收益、高风险”或“低收益、低风险”这些经典规律相违背，如：ED事件驱动指数具有较大的标准差，其平均收益水平却是负的；ES股票多空仓指数的平均收益水平最低，其标准差并非最低.在收益序列的高阶矩统计特征方面，不同对冲基金策略也呈现出异质性，如：FI固定收益方向型策略具有最大的偏度和最高的峰度，表明一方面该基金策略收益高于平均收益的可能性较大；另一方面其收益取得极值的可能性较大，呈现出严重的非正态特征，J-B检验结果也证实了这一点.此外，所有策略指数的超额峰度都大于0，存在极端收益状态.其余对冲基金(如：ES)，J-B检验并不能拒绝其正态性假设，不过其收益还是呈现出非对称性，可以从分位数统计结果得出(如：ES的25%分位数为-0.024 2、中位数为-0.010 0，而75%分位数为0.006 2).这些描述性统计结果要求在研究对冲基金策略指数收益时，不仅需要关注其正常收益能力(与中位点对应)，还需要关注其尾部收益能力(与高、低分位点对应)，分位数回归方法为此提供了有效的工具.在对冲基金收益序列中表现出来的这些统计特征，主要归因于基金经理人所采用的对冲、卖空、贷杠、套利等特殊的投资策略.

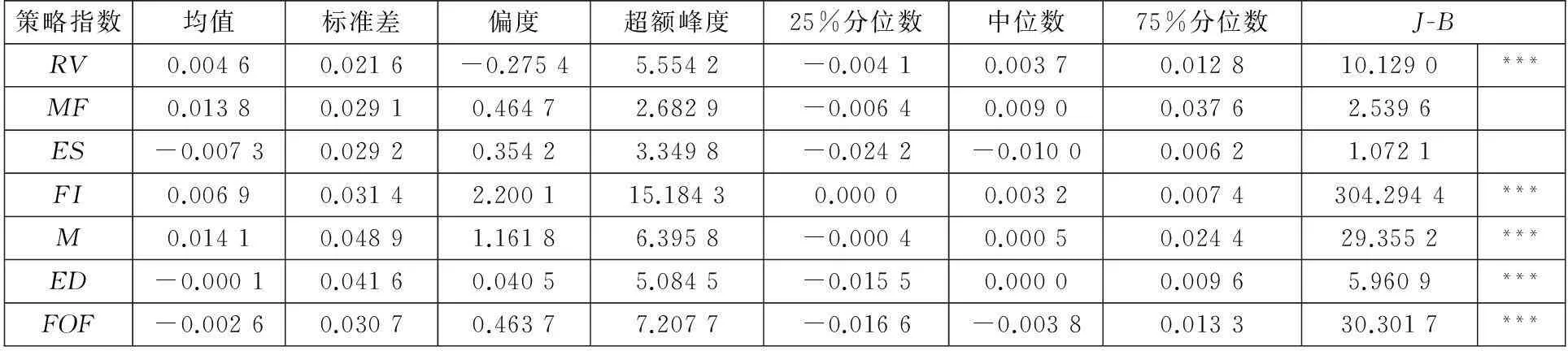
表 1　对冲基金策略指数收益的描述性统计

注：1.J-B检验是由Jarque-Bera提出的，用于检验随机变量是否服从正态分布；

2.***表示在0.1%水平下显著；

3. 超额峰度值是在R3.0.1软件中使用moments包中skewness函数计算的结果，其取值满足：超额峰度=峰度-3，大于0就表明

具有高峰特征，意味着有极大可能性取得极端值.

2.2对冲基金投资风格识别

首先，使用LASSO分位数回归进行变量选择并揭示对冲基金单一策略指数与风险因子之间的关系.为确定LASSO分位数回归模型中惩罚参数λ的取值，使用前文给出的AIC准则.图1给出了AIC值和λ值之间的关系，其中λ值在0到0.1之间变化，5条曲线分别代表在不同分位点处AIC取值.由图1可见，随着λ值增加，AIC值总体上呈下降趋势，并且稳定在某一水平上.表2给出了不同的分位点下，由AIC值确定的最佳λ值.根据最佳λ值，得到LASSO分位数回归模型估计结果(数值略)，表3显示了各风险因子在不同分位点处对每一只对冲基金单一策略指数是否具有显著性影响，其中：“√”表示回归系数不为0，即存在显著性影响.

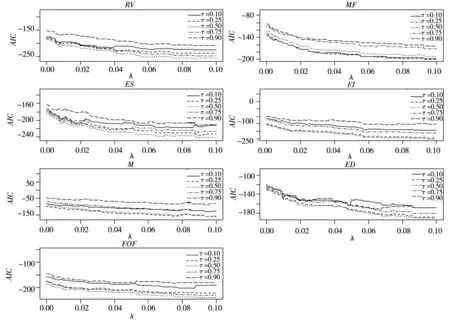
图1　AIC值和λ之间的关系

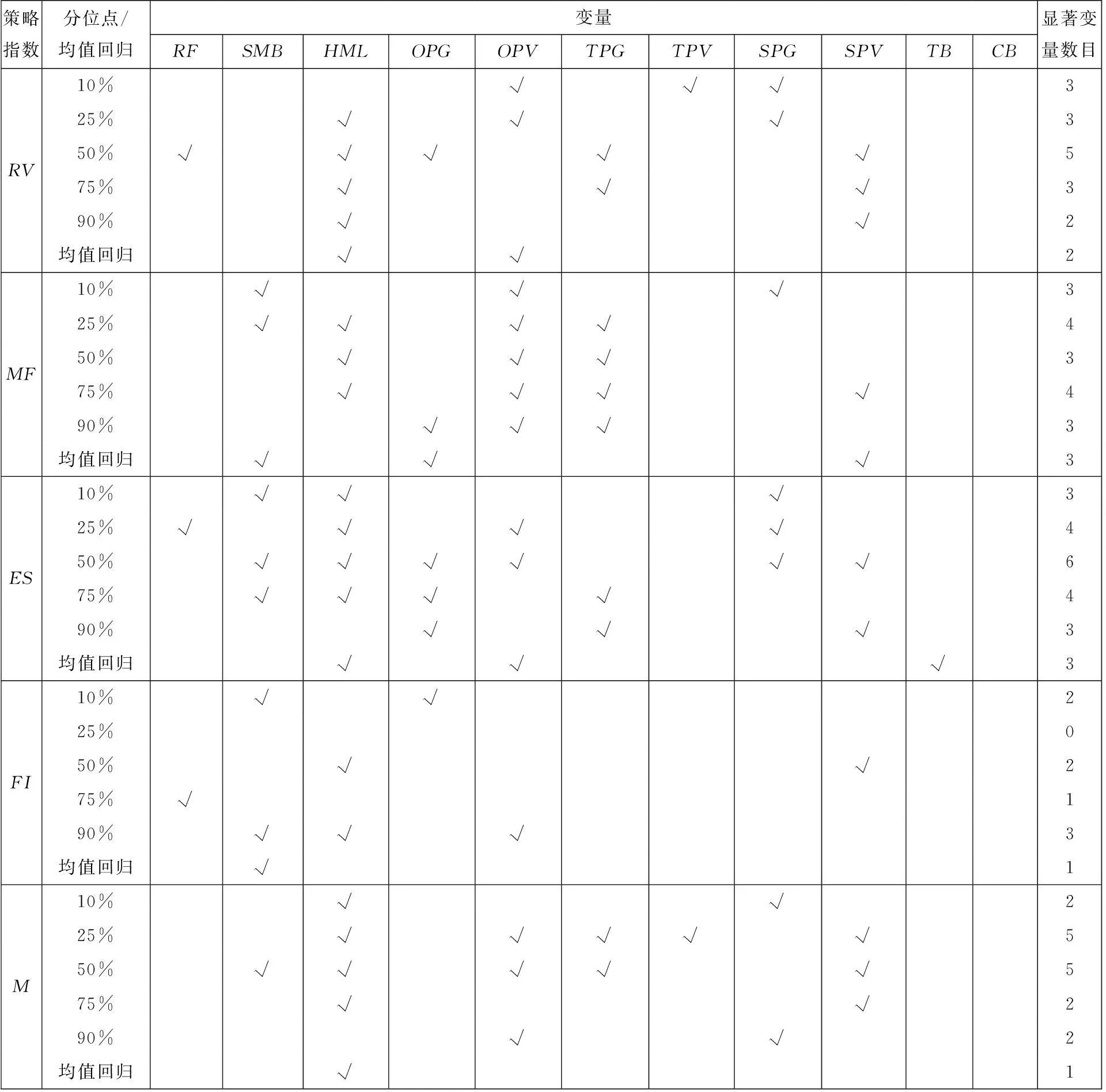
表3　基于均值回归与分位数回归的对冲基金影响因子分析

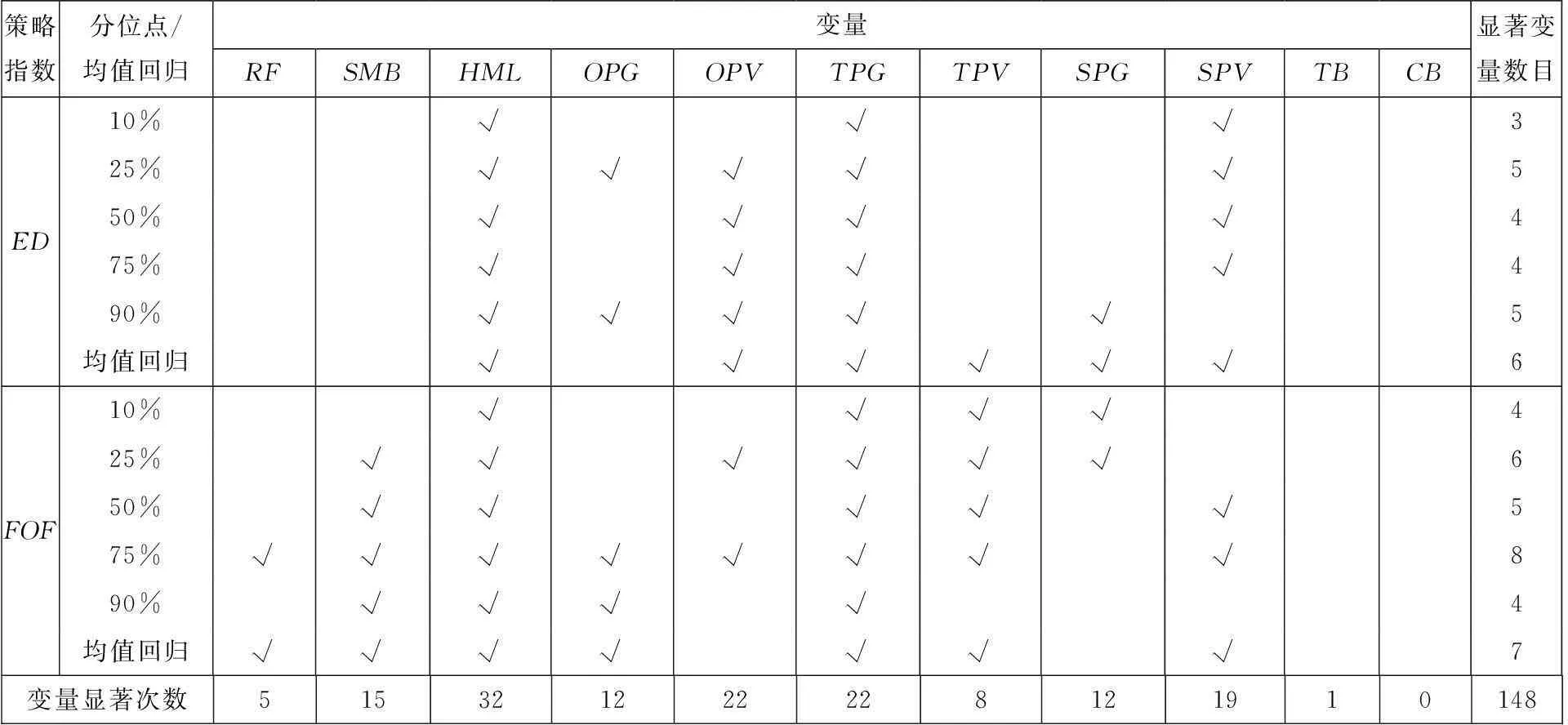
续表3(Table 3 Continue)

注：1.均值回归使用了向前逐步回归法；

2.分位数回归使用了LASSO分位数回归，这里只报告了在分位点为10%、25%、50%、75%和90%的情形.

为比较，在均值回归框架下，使用向前逐步回归，建立风险因子与对冲基金收益之间关系，显著的风险因子也列于表3.由表3可以看出：第一，在不同分位点处，影响对冲基金收益的风险因子存在着显著的差别，如FOF策略指数在高分位点(75%分位点有8个)与低分位点(25%分位点有6个)处受较多的风险因子影响，而在其余分位点显著贡献的风险因子数目较少，表明部分风险因子对收益分布的尾部有显著的影响，这一现象在均值回归模型中得不到反映.第二，在分位数回归的中位点处所得结果和条件均值回归之间也存在着差别，如ES策略指数在中位点处受到6个风险因子的影响，而由于均值回归得到的结果是3个风险因子存在显著影响，这一结果得益于ES策略指数存在严重的非对称性，均值回归很难具有代表性.第三，不同的风险因子显著影响到对冲基金收益的次数也不相同，确定了不同的投资风格，如200纯成长指数(TPG)在所讨论的模型中共有22次显著，表明本文所讨论的对冲基金大多数属于成长型投资风格；而国债指数(TB)与企业债指数(CB)的显著次数都分别为1和0，表明对冲基金大多数没有采用平衡投资风格.

总体来看，在对冲基金收益的整个分布上，分位数回归方法能够更加深入分析对冲基金收益和风险因子之间关联性，它可以捕捉到均值回归模型所遗漏的一些重要信息，从而能够更加准确地识别对冲基金投资风格.

2.3对冲基金投资绩效评价

在识别了对冲基金投资风格以后，可以使用α*指数评价其投资绩效.由式(8)可见，对于基于分位数回归的对冲基金投资绩效评价，依赖风险厌恶参数γ*的取值.Garlappi等[26]取γ*=1，Meligkotsidou等[6]取γ*=2，而Han[27]使用了不同的风险厌恶参数取值，取γ*∈[2,10].考虑到当γ*=0时，有α*=α(0.5)，此时基于分位数回归的投资绩效评价退化为基于中位数回归的投资绩效评价.本文让γ*在0到10范围每隔0.1依次取值，分别计算α*并排序，发现当γ*∈[0,1.4]时，排序结果一致；当γ*∈[1.5,10]时，排序结果也一致，呈现两个阶段，见表4.在表4中，排序1～7表示对冲基金绩效顺序依次递减.由表4可以看到：第一，γ*取值不同对基于分位数回归的排序结果有所影响，呈现两个阶段，不过两个阶段排序结果比较相关(Spearman等级相关系数为0.79)；第二，基于中位数回归的排序结果与基于分位数回归在γ*=0时的排序结果完全一致，不仅如此，与γ*∈[0,1.4]时排序结果也完全一致；第三，基于均值回归的排序结果与基于中位数回归的排序结果几乎一致,而与基于分位数回归的排序结果存在一定的差异，其与中位数回归或分位数回归第1阶段排序结果的Spearman等级相关系数为0.96、与分位数回归第2阶段的Spearman等级相关系数为0.75.

至此，基于分位数回归不仅可以识别对冲基金投资风格，而且可以评价对冲基金投资绩效.不过，仍然无法确定这一投资绩效评价结果是否可靠.下面，将通过构造组合投资的方式，并与经典的组合投资决策模型进行比较，来回答这一问题.

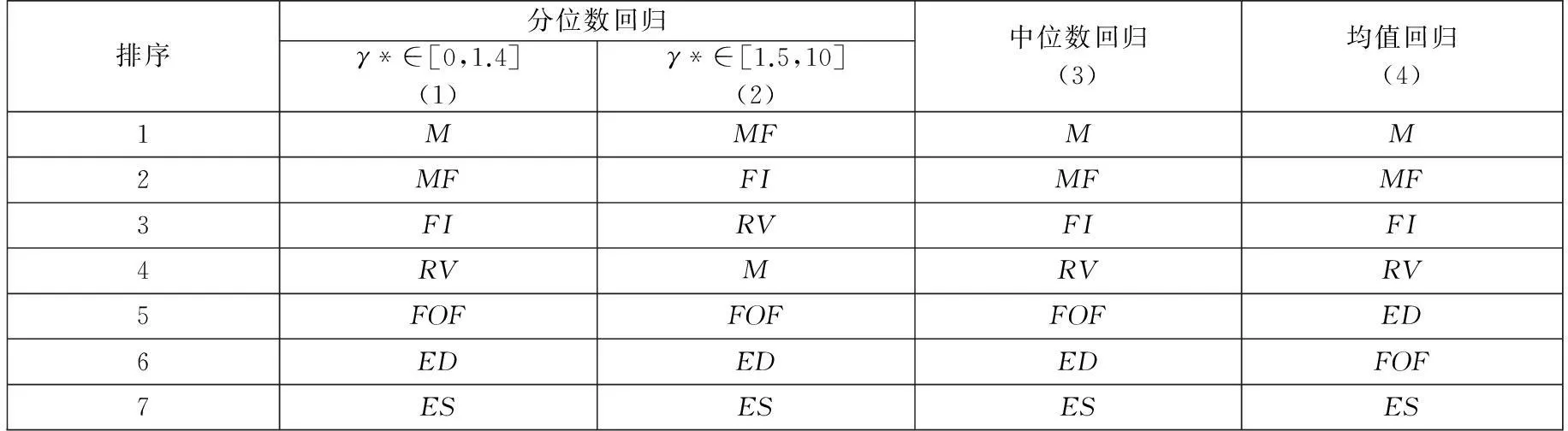
表4　对冲基金投资策略绩效评价

2.4对冲基金风格组合投资决策

在表4所示的单个对冲基金投资策略绩效评价基础上，根据排序结果，按照优选顺序依次赋权，可以构造风格组合投资方案.为验证本文提出方法的稳健性，考虑了3个不同的赋权方案：方案1为“严重偏好”，表示基金经理特别看重绩效好的基金，而忽略绩效差的基金；方案2为“中等偏好”，表示基金经理看重绩效好的基金，也同时考虑绩效差的基金；方案3为“一般偏好”，表示基金经理只是稍微侧重绩效好的基金.这3个赋权方案代表了不同的偏好程度，具有较好的代表性.在权重分配时，使用了等差数列，3个方案的权重大小分别为：(0.229, 0.200, 0.171, 0.143, 0.114, 0.086, 0.057)、(0.207, 0.186, 0.164, 0.143, 0.121, 0.100, 0.079)、(0.186, 0.171, 0.157, 0.143, 0.129, 0.114, 0.100)，如图2所示.图中横坐标轴为对冲基金绩效排序结果，1～7表示对冲基金绩效顺序依次递减；纵坐标轴表示权重大小.

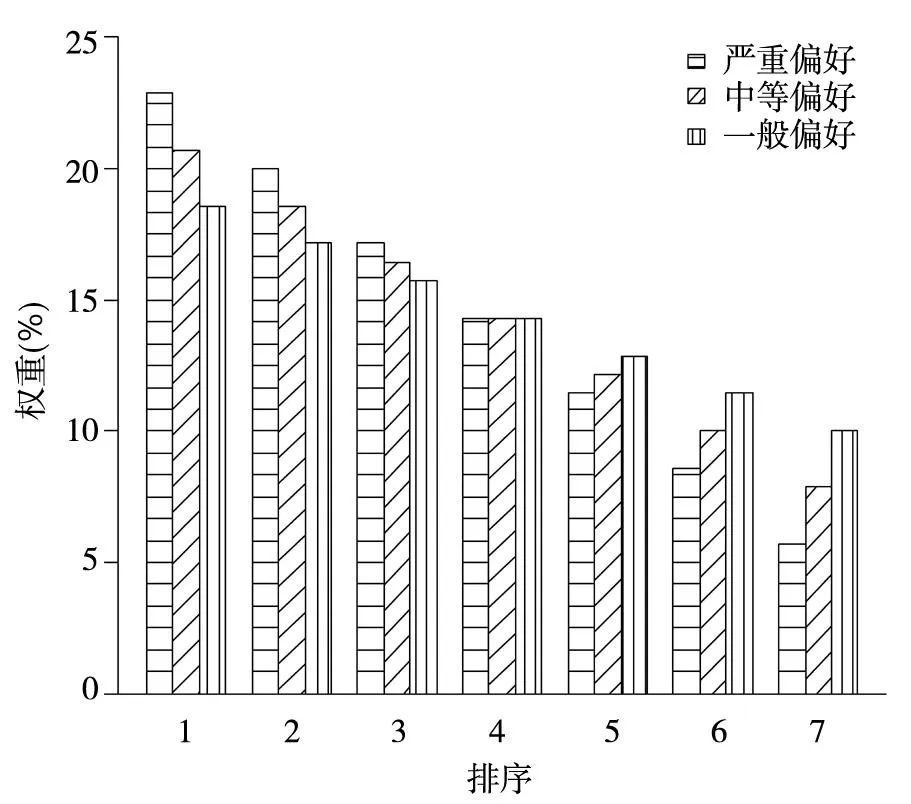
图2权重条形图

Fig. 2 Bar plot of weights

在每一赋权方案下，可以计算出组合投资的平均收益、标准差、下行风险、Sharp比率(ShR)与Sortino比率(SoR)，并且基于分位数回归的评价结果会受到风险厌恶参数γ*的影响，结果见图3.在图3中，实线部分为基于分位数回归所得评价结果，随γ*取值变化，表现为两个阶段；两条虚线分别代表基于中位数回归与基于均值回归所得评价结果，这一结果不受γ*的影响.由图3可知，在不同赋权方案下，由分位数回归所得Sharp比率与Sortino比率起初与中位数回归所得结果一致，随着风险厌恶参数的增加，前者要优于后者，并且两者都比均值回归所得结果理想.

进一步观察，无论在哪一种赋权方案下，基于分位数回归所得Sharp比率与Sortino比率存在最优的风险厌恶参数区间：γ*∈[1.5, 10]，

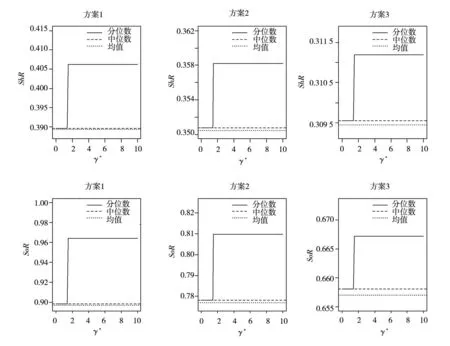
图3风险参数与投资组合绩效关系图

Fig. 3 Relationship between risk parameter and performance of portfolio

表5报告了在最优风险厌恶参数区间中，由分位数回归、中位数回归、均值回归所得的组合投资评价结果.在计算下行风险与Sortino比率时，本文设置参考值RV=0，即可接受的最小投资回报为0.为比较，本文同时考虑了两个经典的组合投资模式：等权组合投资、Markowitz[28]提出的均值-方差模型，并以其作为对比的基准.在基于均值-方差模型求解最优组合投资方案时，本文设置可接受的最小投资回报也为0，目标为最小化标准差.表5也报告了等权组合投资决策与均值-方差模型组合投资决策所得到的相关结果.

由表5可知，第一，就风格组合投资实现的收益而言，基于方案1所得收益均值最高，其次为方案2，再次为方案3，最后为等权组合投资和均值-方差模型，这表明依据分位数回归、中位数回归、均值回归的对冲基金绩效评估结果，选择严重偏好型的组合投资决策，有利于实现对冲基金收益功能.在每个组合投资赋权方案内部，基于均值回归所得收益均值最大，其次为中位数回归，最后为分位数回归.第二，就风格组合投资的风险而言，均值-方差模型所得的标准差风险与下行风险都较小；在不同的赋权方案中，分位数回归所得风险最小，其次为中位数回归，最后为均值回归；等权组合投资所得的风险最大.第三，就风格组合投资的风险调整收益而言，等权组合投资决策获得的Sharp比率与Sortino比率最小、效果最差；在3个赋权方案中，按照Sharp比率从高到低排序依次为：方案1、方案2、方案3，Sortino比率的排序结果与Sharp比率类似.

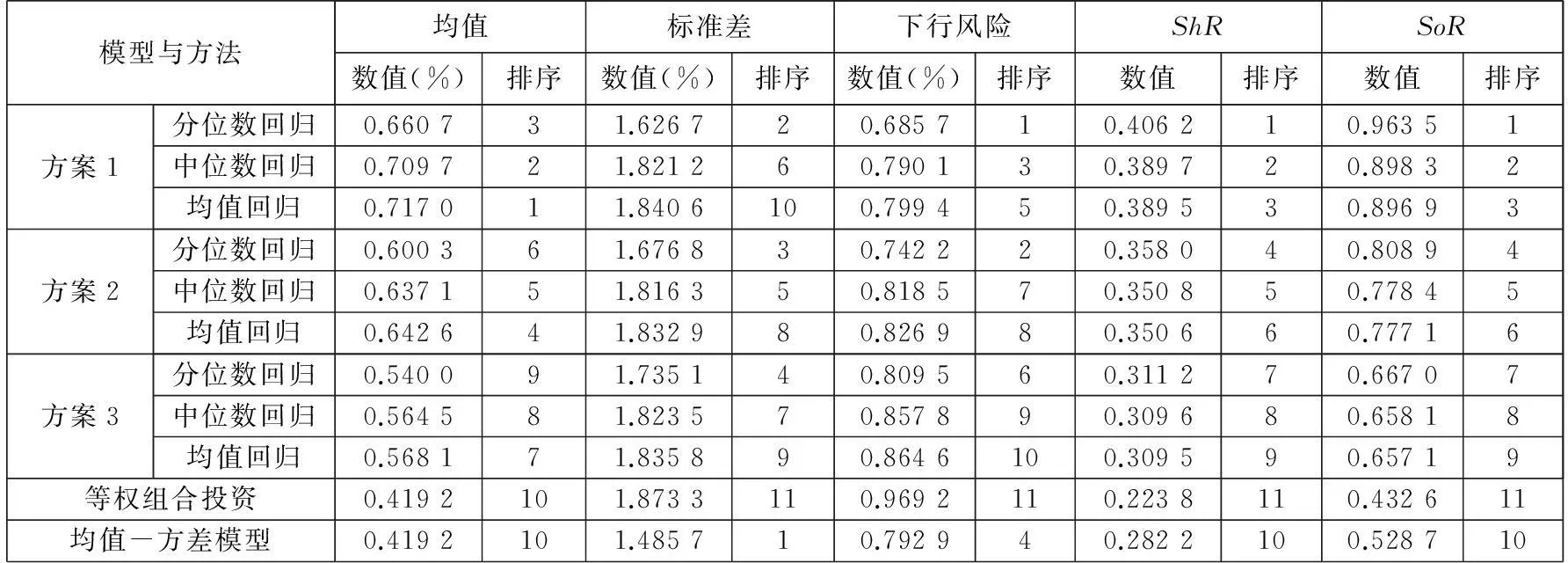
表5　组合投资效果评价

注：1.方案1为严重偏好，方案2为中等偏好，方案3为一般偏好.

2.排序为根据指标属性所得结果，正指标(如：均值、ShR、SoR)取值越大，排序越靠前；逆指标(如：标准差、下行风险)取值越大，排序越靠后.

3稳健性检验

3.1不同参数取值的影响

在前面分析中，已经讨论了不同风险厌恶参数γ*和不同赋权方案的影响，检验了本文提出方法的稳健性.这里，主要讨论式(8)中括号内不同分位点数对(1-τ,τ)的影响，即绩效波动度量方式的影响.为此，在分位点数对(0.25,0.75)的基础上，增加两个分位点数对(0.10,0.90)、(0.15,0.85)的讨论，定义3个α*指数如下

(12)

(13)

(14)

式中α(τ)为LASSO分位数回归模型中截距项在第τ(τ=0.1,0.15,0.25,0.5,0.75,0.85,0.9)分位点处的α估计值，表示绩效的水平；[α(1-τ)-α(τ)]表示绩效的波动，可以视为风险.

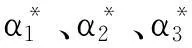
实际上，这一稳健结果有重要的理论基础.Pearson和Tukey[29]发现，对于不同的收益分布形式，对称分位数区间[Q(1-τ)-Q(τ)]与标准差σ之间的比值基本恒定，如：[Q(0.75)-Q(0.25)]/σ≈3.92.这样，本文定义的绩效波动

[α(1-τ)-α(τ)]≈c(τ)σ

(15)

仅仅相差一个依赖于分位点τ的固定常数c(τ).3个α*指数，可以统一表示为类似于均值-标准差(收益-风险)效用函数的形式

(16)

3.2不同极端收益的影响

为考虑不同极端收益的影响，本文选取国际市场的对冲基金作为研究对象.使用本文给出的方法，按照前面的实证过程，研究其投资策略：风格分析、绩效评价、组合投资决策，以检验本文提出方法的稳健性.限于篇幅，这里省略了部分实证过程，只给出实证结果，感兴趣的读者可以来函索取相应的原始数据、计算程序、实证过程和实证结果.

根据Hedge Fund Research(HFR)对冲基金分类体系，将对冲基金划分为5大类，其中一级策略有相对价值套利、股票对冲、事件驱动、宏观和组合基金,每一大类又包含有不同的子策略.选取有代表性的13个对冲基金策略指数，分别为可转换套利指数(CA)、股票放空指数(DSB)、新兴市场指数(EM)、股票市场中性指数(EMN)、事件驱动指数(ED)、财困证券指数(DS)、事件导向多策略指数(EDMS)、风险套利指数(RA)、固定收益套利指数(FIA)、全球宏观指数(M)、股票对冲策略指数(EH)、管理期货指数(MF)、多重策略指数(MS).样本区间为2008-04～2014-02，数据频率为月度数据，数据来源于CREDIT SUISSE.影响因素主要包括：Fama和French的3因子(RF、SMB和HML)、标普500隐含波动率指数(VIX)、罗素3 000股票指数(RUS)、摩根士丹利资本国际世界指数(美国除外)(MXUS)、摩根士丹利资本国际新兴市场指数(MEM)、高盛商品指数(GSCI)和10年期国债利率(TB).样本区间为2008-04～2014-02，数据频率为月度数据，数据分别来源于YAHOO FINANCE、FRED ECONOMIC DATA和http://mba.tuck.dartmouth.edu/pages/faculty/ken.french/Data_Library/f-f_factors.html.

由表6给出的国际市场对冲基金策略指数收益的描述性统计可以看出，部分策略指数(如：EMN、FIA)的偏度系数绝对值、峰度系数远远高于国内市场的对冲基金策略指数，具有更为明显的杠杆效应和极端取值.J-B检验统计量取值更大，结果更为显著，这表明它们更多地拒绝了正态性假定.

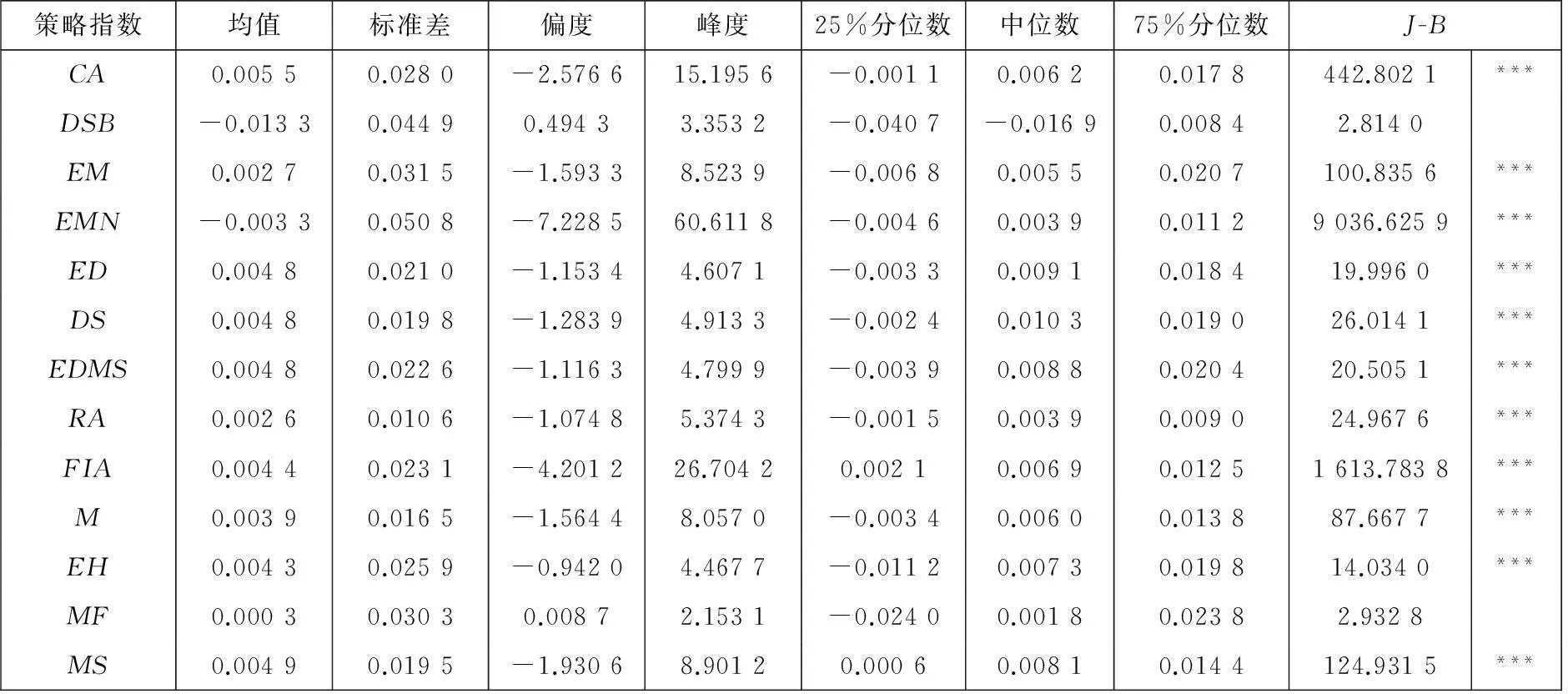
表6　国际市场对冲基金策略指数收益的描述性统计

注：1.J-B检验是由Jarque-Bera提出的，用于检验随机变量是否服从正态分布；

2.***表示在0.1%水平下显著.

3.2.1对冲基金投资风格识别

继续使用LASSO分位数回归进行变量选择并揭示对冲基金单一策略指数与风险因子之间的关系.这里，省略了LASSO分位数回归模型中惩罚参数λ取值及AIC准则取值的报告.表7报告了各风险因子在不同分位点处是否具有显著性影响，其中“√”表示存在显著性影响.

为比较在均值回归框架下使用向前逐步回归，建立风险因子与对冲基金收益之间关系，显著的风险因子也列于表7.由表7可以看出：第一，在不同分位点处，影响对冲基金收益的风险因子存在着显著的差别，如EM策略指数在高分位点处(90%)受较多(9个)的风险因子影响、而在其余分位点显著贡献的风险因子数目较少；FIA策略指数在低分位点处(10%)受较多(9个)的风险因子影响、而在其余分位点显著贡献的风险因子数目较少.第二，在分位数回归的中位点处所得结果和条件均值回归之间也存在着差别，如EM策略指数在中位点处受到4个风险因子的影响，而由均值回归得到的结果是6个风险因子都存在显著影响.第三，不同的风险因子显著影响到对冲基金收益的次数也不相同，确定了不同的投资风格，如GSCI指数在所讨论的模型中共有60次显著，而MXUS指数只有7次显著.

因此，这里所得结论与国内对冲基金投资风格分析所得结论基本一致，分位数回归方法能够更加深入分析对冲基金收益和风险因子在不同分位点处的关联性，能够更加准确地识别对冲基金投资风格，弥补均值回归的不足.

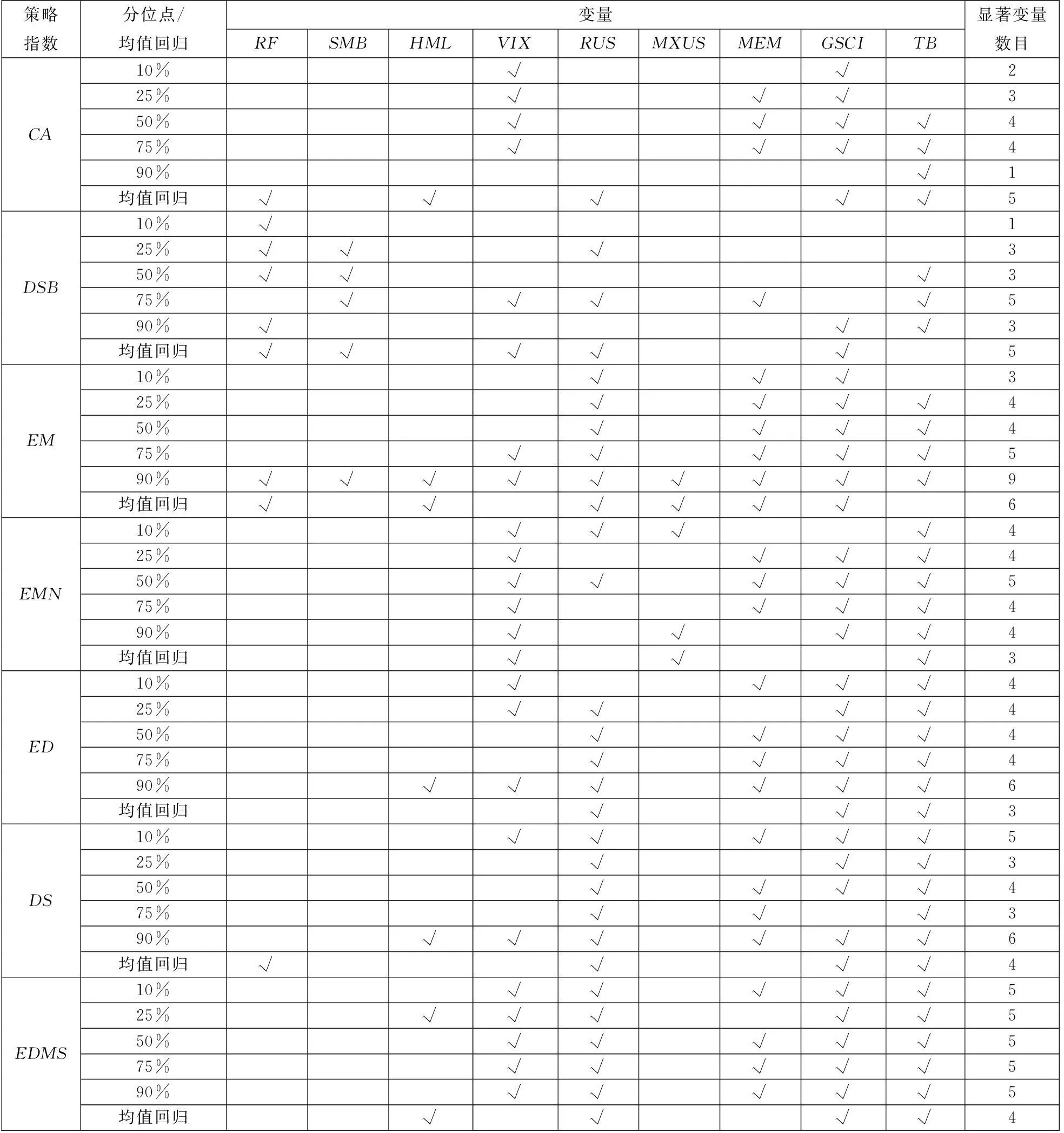
表7　基于均值回归与分位数回归的国际市场对冲基金影响因子分析

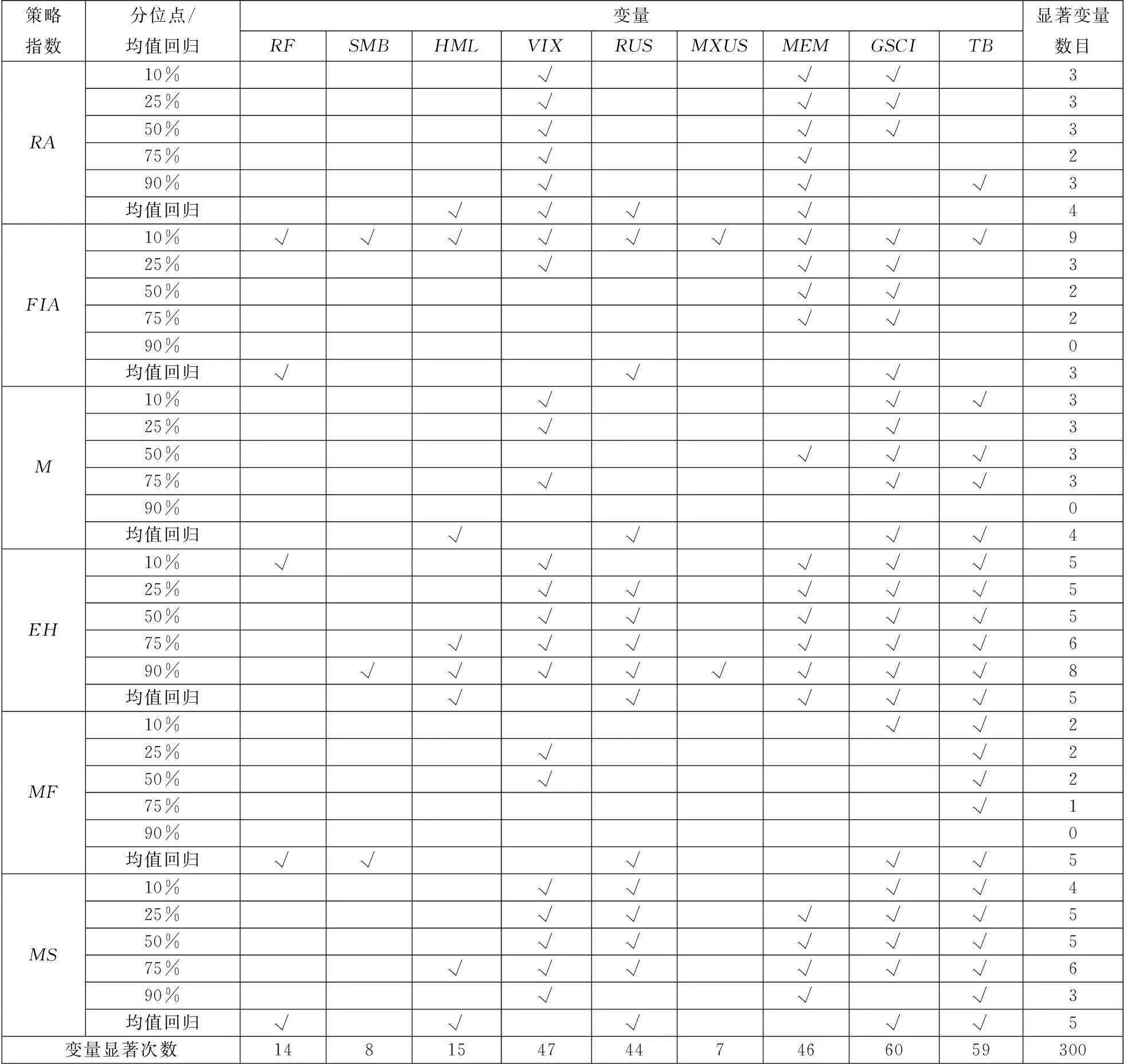
续表7(Table 7 Continue)

注：1.均值回归使用了向前逐步回归法；

3.2.2对冲基金投资绩效评价

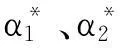
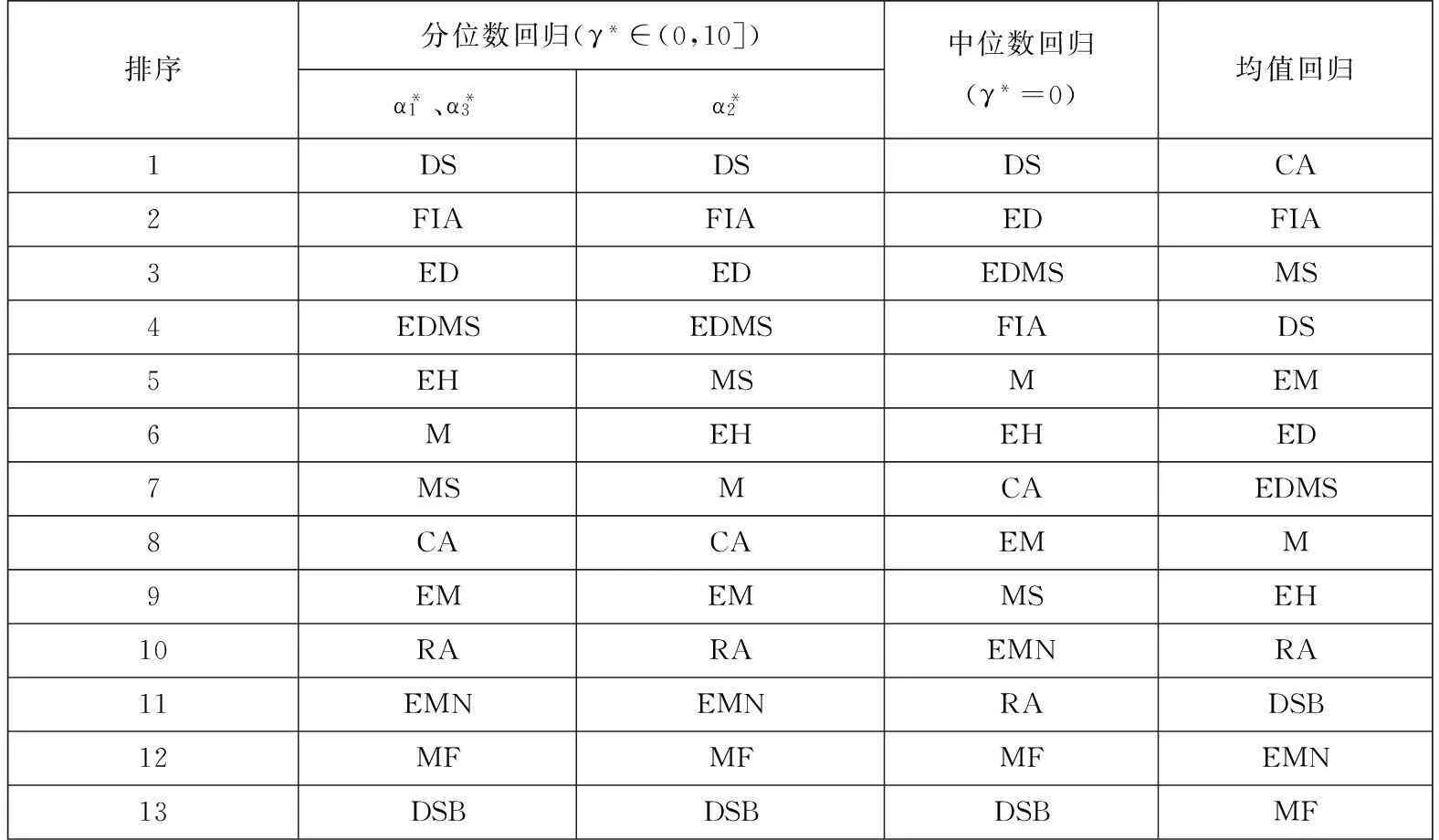
表8　国际市场对冲基金投资策略绩效评价

表9　国际市场对冲基金投资策略绩效排序的Spearman等级相关系

3.2.3对冲基金组合投资决策

在表8所示的单个对冲基金投资策略绩效评价基础上，根据排序结果，按照优选顺序依次赋权，可以构造风格组合投资方案.为验证本文提出方法的稳健性，按照前述权重设计思想，考虑了3个不同的赋权方案，权重大小分别为：(0.154, 0.146, 0.138, 0.123, 0.108, 0.092, 0.077, 0.062, 0.046, 0.031, 0.015, 0.008, 0.000)、(0.146, 0.135, 0.123, 0.112, 0.100, 0.088, 0.077, 0.065, 0.054, 0.042, 0.031, 0.019, 0.008)和(0.131, 0.115, 0.108, 0.100, 0.092, 0.085, 0.077, 0.069, 0.062, 0.054, 0.046, 0.038, 0.023).在每一赋权方案下，可以计算出组合投资的平均收益、标准差、下行风险、Sharp比率(ShR)与Sortino比率(SoR)，结果见图4与图5.

表10和表11报告了由分位数回归、中位数回归、均值回归所得的组合投资评价结果，同时报告了等权组合投资决策与均值-方差模型组合投资决策所得到的相关结果.

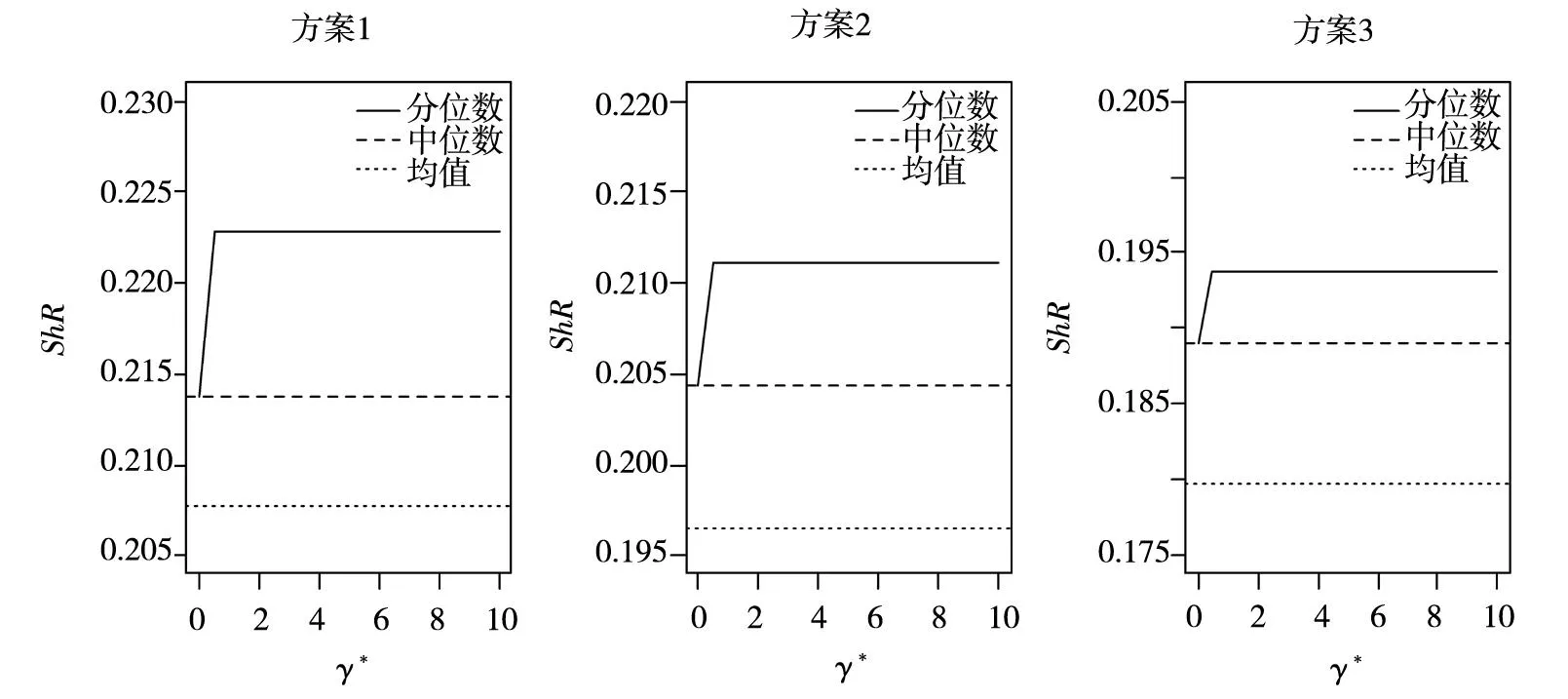
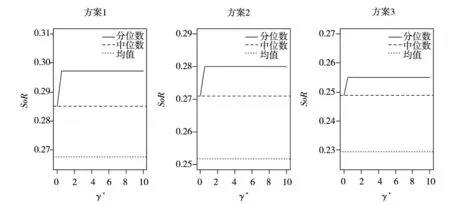
图4　国际市场对冲基金风险参数与投资组合绩效关系图)

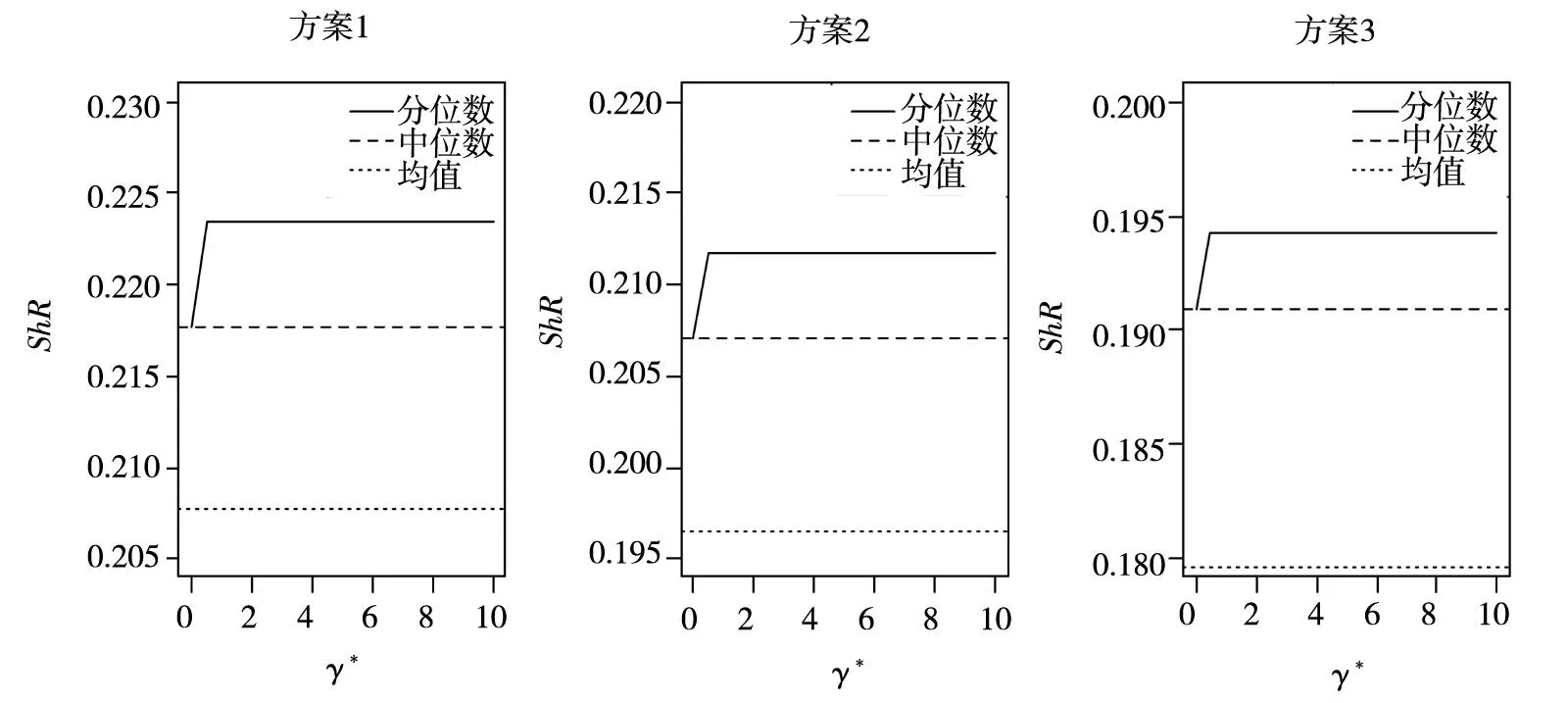
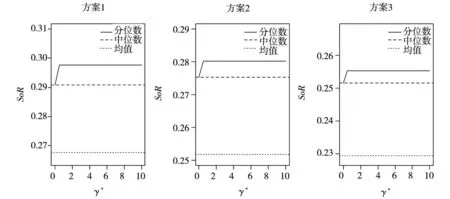
图5　国际市场对冲基金风险参数与投资组合绩效关系图)

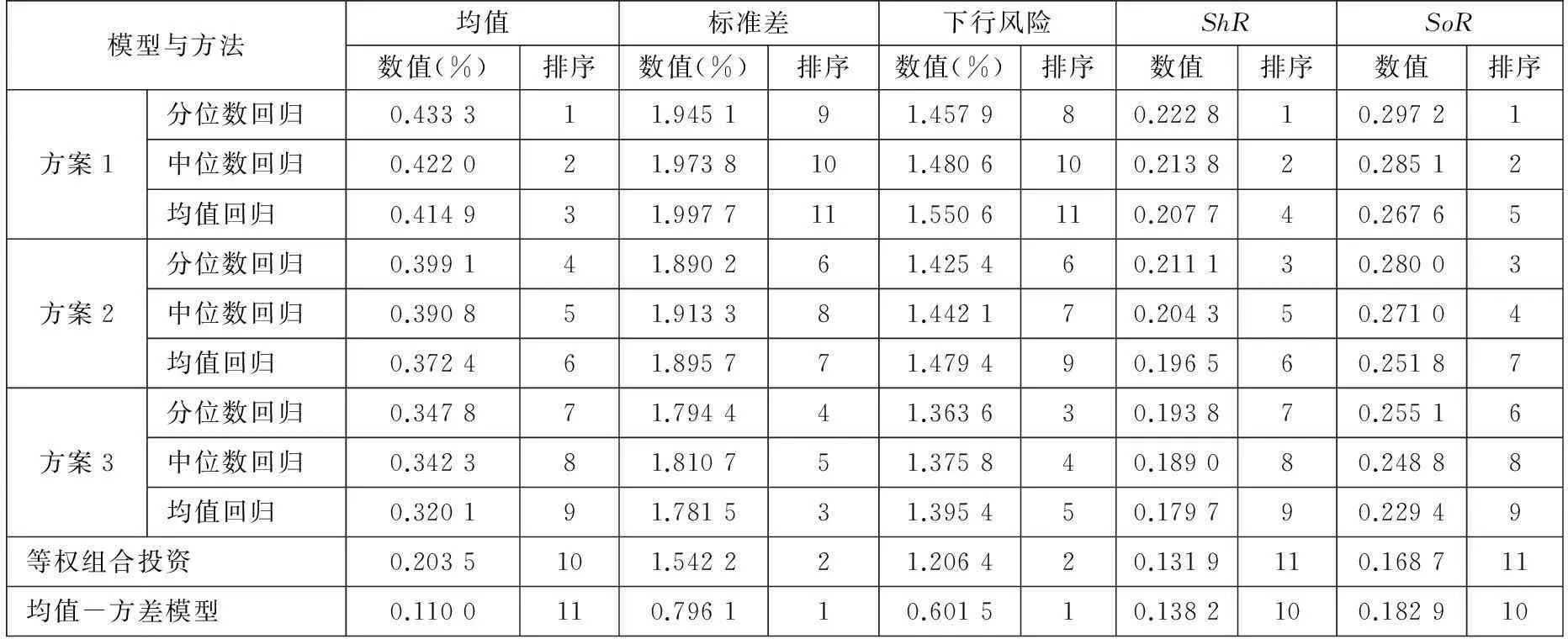
模型与方法均值标准差下行风险ShRSoR数值(%)排序数值(%)排序数值(%)排序数值排序数值排序方案1分位数回归0.433311.945191.457980.222810.29721中位数回归0.422021.9738101.4806100.213820.28512均值回归0.414931.9977111.5506110.207740.26765方案2分位数回归0.399141.890261.425460.211130.28003中位数回归0.390851.913381.442170.204350.27104均值回归0.372461.895771.479490.196560.25187方案3分位数回归0.347871.794441.363630.193870.25516中位数回归0.342381.810751.375840.189080.24888均值回归0.320191.781531.395450.179790.22949等权组合投资0.2035101.542221.206420.1319110.168711均值-方差模型0.1100110.796110.601510.1382100.182910

注： 同表5.

表11　国际市场对冲基金组合投资效果评价(使用排序)

由表10可知，第一，就风格组合投资实现的收益而言，基于方案1所得收益均值最高，其次为方案2，再次为方案3，最后为等权组合投资和均值-方差模型.在每个组合投资赋权方案内部，基于分位数回归所得收益均值最大，其次为中位数回归，最后为均值回归.第二，就风格组合投资的风险而言，均值-方差模型所得的标准差风险与下行风险都较小；在不同的赋权方案中，分位数回归所得风险都较小(除方案3的标准差风险外)，其次为中位数回归，最后为均值回归.第三，就风格组合投资的风险调整收益而言，基于分位数回归方法所得的Sharp比率与Sortino比率最大、效果最好，而等权组合投资模型效果最差；在3个赋权方案中，Sharp比率或Sortino比率从高到低排序依次为：方案1、方案2、方案3.表11给出的组合投资效果排序与表10几乎一致，只是在下行风险这一指标的排序上稍微有所区别.

以上结果与国内对冲基金市场实证结果完全一致，再次表明本文提出的基于LASSO分位数回归对冲基金投资策略研究方法具有较强的稳健性.这主要得益于分位数回归能够细致地刻画在不同分位点处风险因子对于对冲基金收益的不同影响方式，从而能够准确地描述对冲基金收益模式，给出合理的绩效评价结果与组合投资效果.

4结束语

鉴于对冲基金收益分布特征的特殊性，本文提出了基于LASSO分位数回归的对冲基金投资绩效评价方法.这一方法，一方面通过LASSO的变量选择的功能，从影响对冲基金收益的众多风险因子中，挑选出重要风险因子；另一方面，通过分位数回归的功能，细致刻画重要风险因子对对冲基金收益整个条件分布的影响，能够有效地识别对冲基金的投资风格并评价其投资绩效.为验证本文提出方法的有效性，在风格识别与绩效评价的基础上，构建了对冲基金风格组合投资.在与经典的组合投资决策模型(等权组合投资、均值-方差模型、均值回归模型)进行比较过程中，充分考虑了不同的风险厌恶程度与不同赋权方案的影响，实证结果表明：第一，无论是分位数回归，还是中位数回归、均值回归，给出的对冲基金绩效评价结果是有效的，依据该结果进行偏好性的组合投资选择，能够获得较好的风险调整收益；第二，基于LASSO分位数回归给出的组合投资，在选择赋权方案1“严重偏好”时，能够获得最佳的风险调整收益，随后为中位数回归、均值回归；第三，基于均值-方差模型得到的组合投资风险调整收益水平，大体介于赋权方案2“中等偏好”与赋权方案3“一般偏好”之间，而等权组合投资所得组合投资风险调整收益水平最差，意味着消极的等权组合投资选择方案在积极的对冲基金市场上往往难以奏效；第四，本文提出的基于LASSO分位数回归的对冲基金投资策略研究方法具有较强的稳健性，能够满足不同风险偏好(组合投资权重、风险厌恶参数)、不同绩效评价α*指数(分位点数对)、不同极端收益对冲基金(偏度系数、峰度系数)的要求.

以上实证结果的经济意义在于，基于LASSO分位数回归给出的对冲基金投资绩效评价是有效的，依据该评价结果进行偏好性的组合投资选择，就能够取得最佳的风险调整收益，得到满意的投资结果.本文的实证结果是在对冲基金市场上取得的.毫无疑问，本文的方法既可以推广到一般的基金投资策略研究，如共同基金等；也可以推广到更一般的金融市场，进行更广义的组合投资选择(如：股票、债券等)与绩效评价.

参 考 文 献:

[1]Fung W, Hsieh D A. A primer on hedge funds[J]. Journal of Empirical Finance, 1999, 6(3): 309-331.

[2]许启发, 蒋翠侠. 分位数局部调整模型及应用[J]. 数量经济技术经济研究, 2011, 28(8): 115-133.

Xu Qifa, Jiang Cuixia. Quantile partial adjustment model and its application[J]. Journal of Quantitative & Technical Economics, 2011, 28(8): 115-133. (in Chinese)

[3]Koenker R, Bassett G W. Regression quantiles[J]. Econometrica, 1978, 46(1): 33-50.

[4]Yu K, Lu Z, Stander J. Quantile regression: Applications and current research areas[J]. Journal of the Royal Statistical Society: Series D, 2003, 52(3): 331-350.

[5]Bassett G W, Chen H L. Portfolio style: Return-based attribution using quantile regression[J]. Empirical Economics, 2001, 26(1): 293-305.

[6]Meligkotsidou L, Vrontos I D, Vrontos S D. Quantile regression analysis of hedge fund strategies[J]. Journal of Empirical Finance, 2009, 16(2): 264-279.

[7]Tibshirani R. Regression shrinkage and selection via the lasso[J]. Journal of the Royal Statistical Society: Series B, 1996, 58(1): 267-288.

[8]李根, 邹国华, 张新雨. 高维模型选择方法综述[J]. 数理统计与管理, 2012, 31(4): 640-658.

Li Gen, Zou Guohua, Zhang Xinyu. Model selection for high-dimensional data: A review[J]. Application of Statistics and Management, 2012, 31(4): 640-658. (in Chinese)

[9]Koenker R, Ng P, Portnoy S. Quantile smoothing splines[J]. Biometrika, 1994, 81(4): 673-680.

[10]Wang H. Robust regression shrinkage and consistent variable selection through the LAD-Lasso[J]. Journal of Business & Economic Statistics, 2007, 25(3): 347-355.

[11]李熠熠, 潘婉彬, 缪柏其. 基于 LAD-Lasso 方法的利率期限结构拟合中的节点选择[J]. 中国科学技术大学学报, 2010, 40(6): 551-556.

Li Yiyi, Pan Wanbin, Liao Baiqi. Knot selection of estimating the term structure with cubit spline function based on LAD-Lasso criterion[J]. Journal of University of Science and Technology of China, 2010, 40(6): 551-556. (in Chinese)

[12]Li Y, Zhu J. L1-norm quantile regression[J]. Journal of Computational and Graphical Statistics, 2008, 17(1): 163-185.

[13]Lamarche C. Robust penalized quantile regression estimation for panel data[J]. Journal of Econometrics, 2010, 157(2): 396-408.

[14]Belloni A, Chernozhukov V.1-penalized quantile regression in high-dimensional sparse models[J]. Annals of Statistics, 2011, 39(1): 82-130.

[15]李翰芳, 罗幼喜, 田茂再. 面板数据的贝叶斯Lasso分位回归方法[J]. 数量经济技术经济研究, 2013, 30(2): 138-149.

Li Hanfang, Luo Youxi, Tian Maozai. Bayesian lasso quantile regression for panel data models[J]. Journal of Quantitative & Technical Economics, 2013, 30(2): 138-149. (in Chinese)

[16]Jensen M C. The performance of mutual funds in the period 1945-1964[J]. Journal of Finance, 1968, 23(2): 389-416.

[17]蒋翠侠, 张世英. 多元广义自回归条件密度建模及应用[J]. 管理科学学报, 2009, 12(1): 82-92.

Jiang Cuixia, Zhang Shiying. Multivariate generalized autoregressive conditional density modeling and its application[J]. Journal of Management Sciences in China, 2009, 12(1): 82-92. (in Chinese)

[18]Portnoy S, Koenker R. The Gaussian hare and the Laplacian tortoise: Computability of squared-error versus absolute-error estimators[J]. Statistical Science, 1997, 12(4): 279-300.

[19]Efron B, Hastie T, Johnstone I, et al. Least angle regression[J]. Annals of Statistics, 2004, 32(2): 407-499.

[20]Amin G S, Kat H M. Hedge fund performance 1990-2000: Do the “Money Machines” really add value?[J]. Journal of Financial and Quantitative Analysis, 2003, 38(2): 251-274.

[21]Sharpe W F. Mutual fund performance[J]. Journal of Business, 1966, 39(1): 119-138.

[22]Sharpe W F. The Sharpe ratio[J]. Journal of Portfolio Management, 1994, 21(1): 49-58.

[23]陈收, 杨宽, 吴启芳, 等. 投资基金绩效评价的 Sharpe 指数与衰减度实证分析[J]. 管理科学学报, 2003, 6(3): 79-85.

Chen Shou, Yang Kuan, Wu Qifang, et al. Empirical analysis of performance for investment fund through Sharpe ratio and decay rate[J]. Journal of Management Sciences in China, 2003, 6(3): 79-85. (in Chinese)

[24]Sortino F A, Van Der Meer R. Downside risk[J]. Journal of Portfolio Management, 1991, 17(4): 27-31.

[25]Sortino F A, Price L N. Performance measurement in a downside risk framework[J]. Journal of Investing, 1994, 3(3): 59-64.

[26]Garlappi L, Uppal R, Wang T. Portfolio selection with parameter and model uncertainty: A multi-prior approach[J]. Review of Financial Studies, 2007, 20(1): 41-81.

[27]Han Y. Asset allocation with a high dimensional latent factor stochastic volatility model[J]. Review of Financial Studies, 2006, 19(1): 237-271.

[28]Markowitz H. Portfolio selection[J]. Journal of Finance, 1952, 7(1): 77-91.

[29]Pearson E S, Tukey J W. Approximate means and standard deviations based on distances between percentage points of frequency curves[J]. Biometrika, 1965, 52(3/4): 533-546.

Hedge fund investment strategies based on LASSO quantile regression

JIANGCui-xia1, 2,LIUYu-ye1,XUQi-fa1, 2

1. School of Management, Hefei University of Technology, Hefei 230009, China;2. Key Laboratory of Process Optimization and Intelligent Decision-making, Ministry of Education, Hefei University of Technology, Hefei 230009, China

Abstract:The return of hedge funds often has different statistical characteristics and risk return relations from those of regular investments due to the fact it adopts some flexible investment skills in practice. Therefore, it is difficult to evaluate the performance of hedge funds by using some traditional methods. Based on LASSO quantile regression, the paper identifies some important risk factors, which are helpful to explain hedge fund investment style, and provides a new method by considering the relationship between return and risk across quantiles to evaluate the performance of hedge funds. For illustration, a style portfolio of hedge funds is constructed through LASSO quantile regression. Then, the style portfolio is compared with some classical methods for portfolio choice, such as mean regression portfolio, equal-weighted portfolio, and Markowitz portfolio. Empirical results show that our evaluation method based on LASSO quantile regression is relatively effective and its portfolio investment scheme may obtain higher risk adjusted returns.

Key words:hedge fund; LASSO quantile regression; hedge fund performance; style portfolio

中图分类号:F224

文献标识码:A

文章编号:1007-9807(2016)03-0107-20

作者简介:蒋翠侠(1973—)， 女， 安徽砀山人， 博士， 副教授， 硕士生导师. Email: jiangcx1973@163.com

基金项目：国家社会科学基金一般资助项目(15BJY008)； 国家自然科学基金资助项目(71071087)； 教育部人文社会科学研究规划基金资助项目(14YJA790015)； 安徽省哲学社会科学规划基金资助项目(AHSKY2014D103)； 山东省科技发展计划资助项目(2014GGX101055).

收稿日期：(①) 2014-01-09；

修订日期：2014-11-29.