在马尔科夫转换下有着随机选取斑块的单种群间歇扩散模型∗
李宝雄,张龙,年巧玲
(新疆大学数学与系统科学学院,新疆乌鲁木齐830046)
0 引言
种群扩散在自然环境中是普遍存在的一种现象,它在种群的生存和演化过程中扮演着重要的角色.许多作者已经很好地研究了关于种群扩散的文献,同时,斑块环境下的单种群动力系统也被做了更好地探究[1−4].例如,Cui和Chen[1]考虑了如下的斑块环境下的单种群扩散系统:
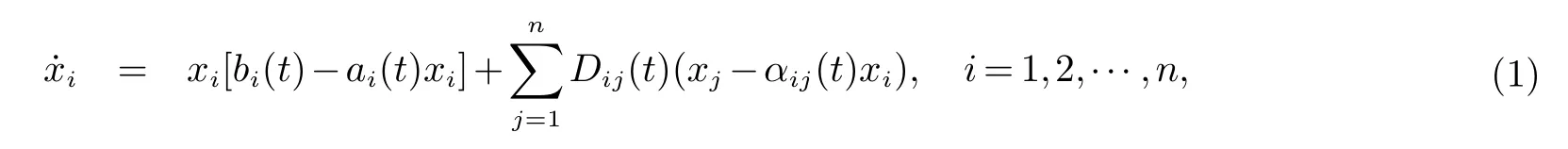
这是一个双向扩散系统,作者讨论了正周期解的存在唯一性及其全局稳定性.
上述讨论的都是确定性系统,并且总是假定系统中的系数与环境的波动起伏无关.然而,在自然环境中,种群扩散通常不可避免地受到环境噪声的影响.一般地,有很多种环境噪声,电报声是其中之一,它是一种在两个或者更多环境体制中的转换形式,近年来,很多学者研究了在体制转换下系统正解的全局存在性,随机持久性以及灭绝性[5−8].
遗憾的是,在上述所有的随机种群系统中,很少有作者讨论体制转换下的种群扩散现象.此外,在现实的生态系统中,由于受到季节的更替或者其他环境因素的影响,任意两个斑块间的种群扩散行为会发生在一段固定的时间,即间歇扩散行为,而这种扩散现象广泛地存在于自然界之中.
基于上述思考,我们提出了如下的在三个斑块间具有马尔科夫转换的间歇扩散单种群系统:

此模型假设种群x=(x1,x2,x3)T由三个斑块组成,当t∈(τ2k,τ2k+1]时,斑块xr1(τ2k)(t),xr2(τ2k)(t)的阀门打开,并且这两个斑块中的种群开始从一个斑块扩散到另一个斑块,斑块xr3(τ2k)(t)中的种群不会有扩散行为发生,当t∈(τ2k+1,τ2k+2]时,生活在每个斑块中的种群都不会有扩散行为发生.其中,(i){rj(t),t≥τ0>0,且当t=τ2k(k∈N),ri(τ2k)6=rj(τ2k),i,j=1,2,3,i6=j}是定义在全概率空间(Ω,F,P)上的右连续马尔科夫链,并且取值在有限状态空间S={1,2,3}.此外,r1(τ2k)与r2(τ2k)是随机选择的进行互相扩散的的两个斑块,r3(τ2k)是不进行扩散的斑块.
(ii)xrj(τ2k)(t)是第rj(τ2k)斑块中种群的密度,a(rj(t))(或˜a(rj(t)))是第rj(τ2k)斑块中的种群在区间(τ2k,τ2k+1](或(τ2k+1,τ2k+2])上的内禀增长率,b(rj(t))(或˜b(rj(t)))是第rj(τ2k)斑块中的种群在区间(τ2k,τ2k+1](或(τ2k+1,τ2k+2])上的密度制约系数,Dr1(τ2k)r2(τ2k)(r1(t))代表种群在时间区间(τ2k,τ2k+1]从r2(τ2k)斑块到r1(τ2k)斑块的扩散系数,Dr2(τ2k)r1(τ2k)(r1(t))代表种群在时间区间(τ2k,τ2k+1]从r1(τ2k)斑块到r2(τ2k)斑块的扩散系数,且满足:0 贯穿全文,设(Ω,F,{Ft}t≥0,P)是一个全概率空间且有着一个滤子{Ft}t≥0满足通常条件(即它是右连续的且包含所有的P-空集).同时,假设斑块ri(t)与斑块rj(t)(i,j=1,2,3,i 6=j)在同一时刻有着相同的转移速率,则可以将一维的马尔科夫链推广到三维的情形,即设{r(t)=(r1(t),r2(t),r3(t))T,t≥0}是一个定义在概率空间(Ω,F,{Ft}t≥0,P)上的右连续的马尔科夫链,并且在有限状态空间˜S上取值,满足生成元Π=(πIJ)6×6: 其中, I,J∈πIJ是从状态I到状态J的转移速率,并且πIJ≥0(I,J∈˜S,I 6=J),同时有 其次,给出如下的术语. R3为三维实数空间,x为三维列向量,其转置为表示正锥且有xi>0,∀1≤i≤3},R+表示开区间且有R+=(0,∞),N表示自然数集,Λ表示时间区间且有表示欧氏范数,∅代表空集. 为了方便起见,定义有界函数f(ri(t))与gri(τ2k)rj(τ2k)(ri(t))(i,j=1,2,3,k∈N)满足: 再次,引入一些有用的定义及引理. 定义1[9]称系统(2)是随机最终有界的,如果对于任意的ε∈(0,1),存在一个正数δ=δ(ε),使得满足初值的解x(t)有着如下的属性: 引理1[10](切比雪夫不等式)如果c>0,p>0,x∈Lp,则 最后,为了更加方便研究,记 则将方程(2)转化为如下的矢量的形式: 其中, 基于对模型的讨论,可以做出如下的基本假设: (H1)设是关于t∈Λ的有界可积函数,且有b(rj(t)),˜b(rj(t))>0(j=1,2,3,k∈N).(H2)设 且满足 定理1假设基本假设(H1),(H2)成立,则系统(2)满足初始条件的解xr(τ2k)(t)依概率1停留在中,即对所有的t∈Λ几乎必然成立. 证明易得系统(2)的系数关于xr(τ2k)(t)满足局部李氏条件,则在是爆炸时刻)上有一个唯一的最大局部解,并且易证系统(2)满足初始条件的解上是正的.下证σe=∞a.s.即可. 设K0>0足够大,使得的每一部分都不会超过K0.对于每个整数K≥K0,定义如下的停时 并且约定inf∅=∞.显然,当K→∞时,σK是递增的.设σ∞=limK→∞σK,则σ∞≤σea.s.因此,只需证σK=∞a.s.如若不然,则存在一对数T>0与ε∈(0,1)使得 定义函数V 其中是一个正数.除此之外,函数V满足:当t=τ2k(k∈N)时,I=r(τ2k),当t6=τ2k(k∈N)时,I 6=r(τ2k). 对于上述的K≥0,存在一个iK使得则有如下的两种情形: 情形1当iK∈G={m|m=2n+1,n∈N+}时, 设 通过推广的Itˆo公式及(9),可得 其中,LV是的映射,C是一个正常数,并且有 对于σK∈(τiK−1,τiK](iK∈G)及T>0,对(10)从到σK∧T进行积分并取期望得 由于 则通过(8),(11),(12),基本假设(H2)与格朗沃尔不等式可得 因此,由(6),(7)以及(13)可得 让K→∞,则有 这就产生了矛盾. 情形2当时,同理可得σ∞=∞a.s..即系统(2)满足初始条件的解xr(τ2k)(t)依概率1停留在中. 定理2假设基本假设(H1),(H2)成立,则系统(2)满足初始条件的任何正解xr(τ2k)(t)是随机最终有界的,即 证明由定理1知,系统(2)存在满足初始条件的全局正解.定义函数V:R3+טS→R+ 其中cm(I)(m=1,2,3,I∈˜S)是一个正数.此外,函数V满足:当t=τ2k(k∈N)时,I=r(τ2k),当t6=τ2k(k∈N)时,I 6=r(τ2k). 因此,对任意的t∈(τk−1,τk]∪(τk,τk+1],有以下两种情形: 情形1当k∈G={m|m=2n+1,n∈N+}时,对etV(xr(τ2k),I)运用推广的Itˆo公式 其中L(etV)是的映射,且有 对任意的t∈(τk−1,τk](k∈G),对(18)式从到t积分并取期望得 由于 并且记 则通过(17),(19),(20),(21),基本假设(H2),同时运用归纳法可得 注意到 其中v=min{cm(I):1≤m≤3,I∈˜S}. 通过(22),(23)可得 情形2当k∈¯G={m|m=2n+2,n∈N}时,同理可得,存在H2>0使得 综上所述,对任意的t∈(τk−1,τk](k∈N),存在H=max{H1,H2}>0,使得 因此,对任意的ε∈(0,1),取运用切比雪夫不等式可得 故 则系统(2)是随机最终有界的. 参考文献: [1]Cui J,Chen L.Permanence and extinction in Logistic and Lotka-Volterra system with diffusion[J].Journal of Mathematical Analysis and Applications,2001,258(2):512-535. [2]Teng Z,Lu Z.The effect of dispersal on single-species nonautonomous dispersal models with delays[J].Mathematical Biology,2001,42(5):439-454. [3]Hui J,Chen L.A single species model with impulsive diffusion[J].Acta Mathematicae Applicatae Sinica.2005,28(1):43-48. [4]Zhang L,Teng Z.Single species models with logistic growth and dissymmetric impulse dispersal[J].Mathematical Biosciences,2013,241:188-197. [5]Tan R,Liu Z.On a non-autonomous competitive system subject to stochastic and impulsive perturbations[J].Applied Mathematics and Computation,2015,256:702-714. [6]Lv J,Wang K.Almost sure permanence of stochastic single species models[J].Journal of Mathematical Analysis and Applications,2015,422:675-683. [7]Li X,Jiang D.Population dynamical behavior of Lotka-Volterra system under regime switching[J].Journal of Computational and Applied Mathematics,2009,232:427-448. [8]Liu Z,Zhong S,Teng Z.n Species impulsive migration model with Markovian switching[J].Journal of theoretical biology,2012,307:62-69. [9]Li X,Gray A.Sufficient and necessary conditions of stochastic permanence and extinction for stochastic logistic populations under regime switching[J].Journal of Mathematical Analysis and Applications,2011,376:11-28. [10]Mao X,Yuan C.Stochastic differential equations with Markovian switching[M].London:Imperial College Press,2006.1 预备知识
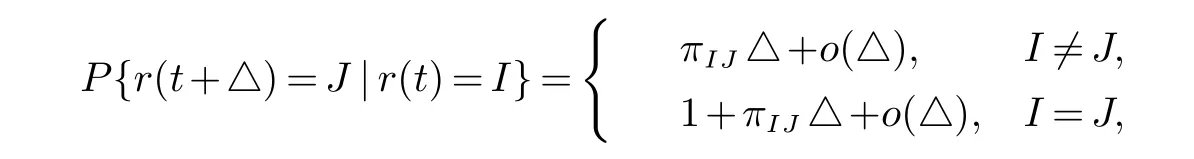
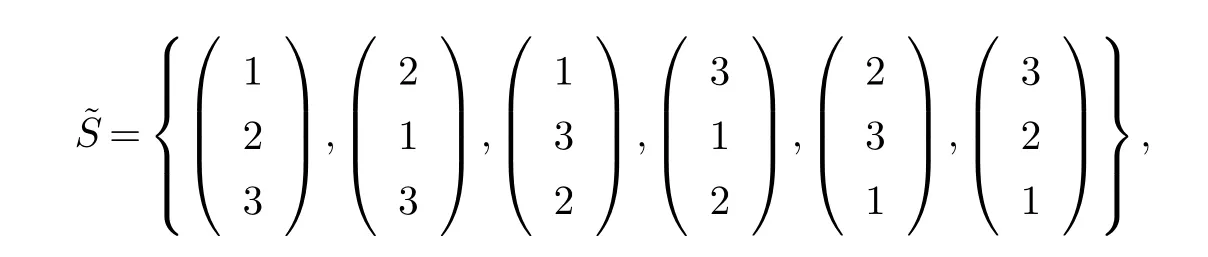
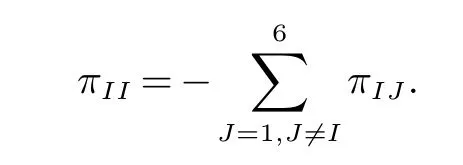
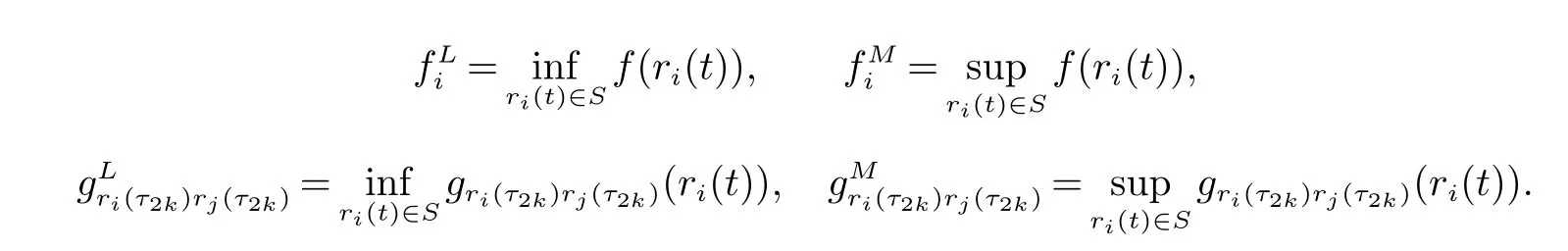


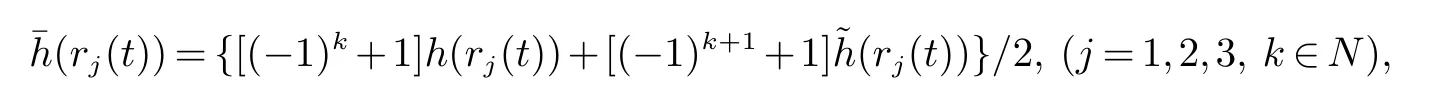
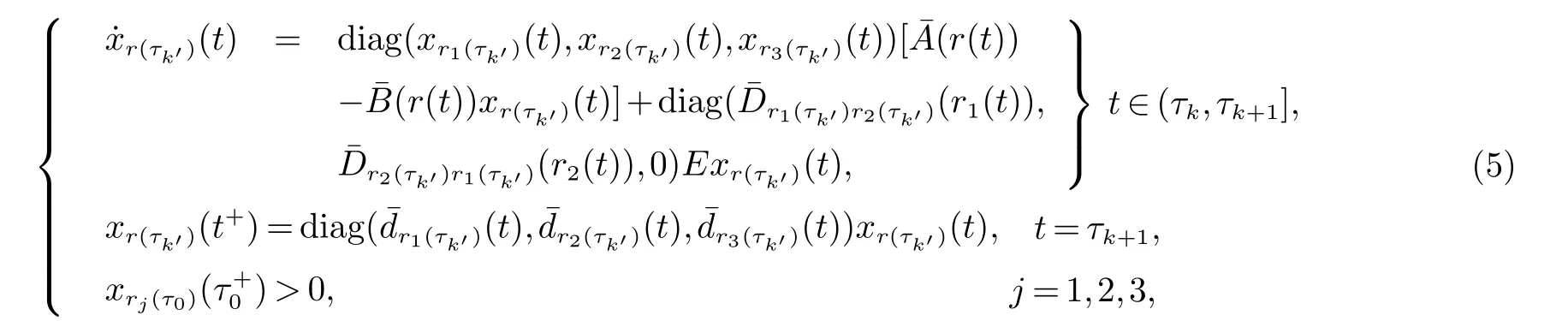

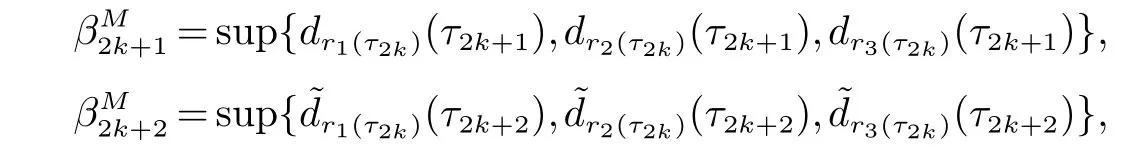
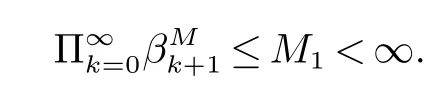
2 主要结果


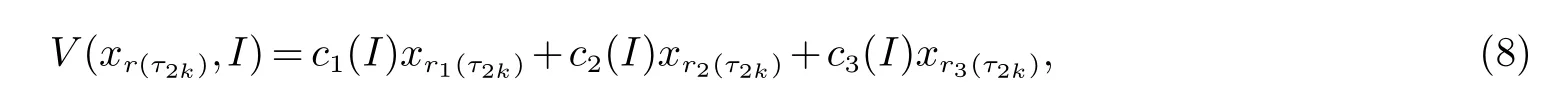
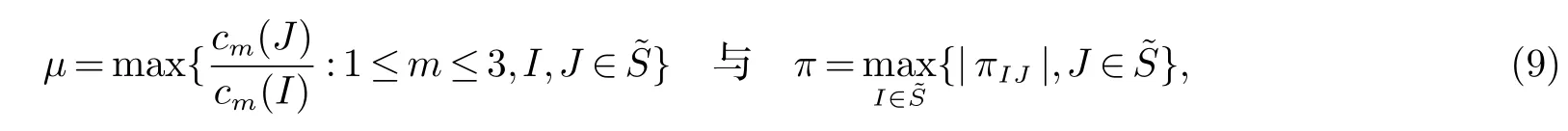
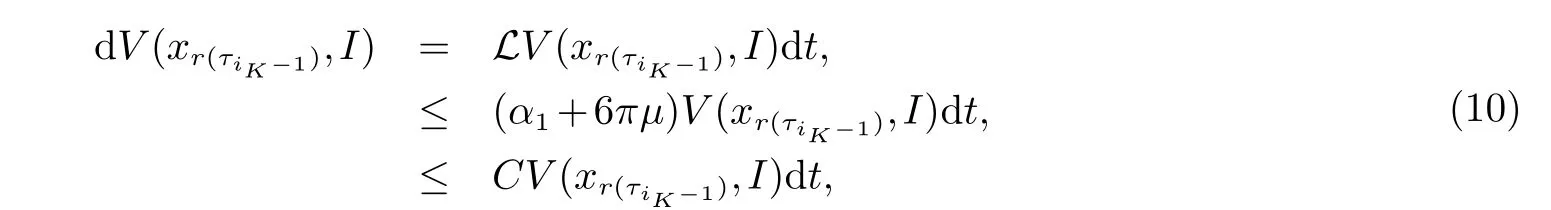
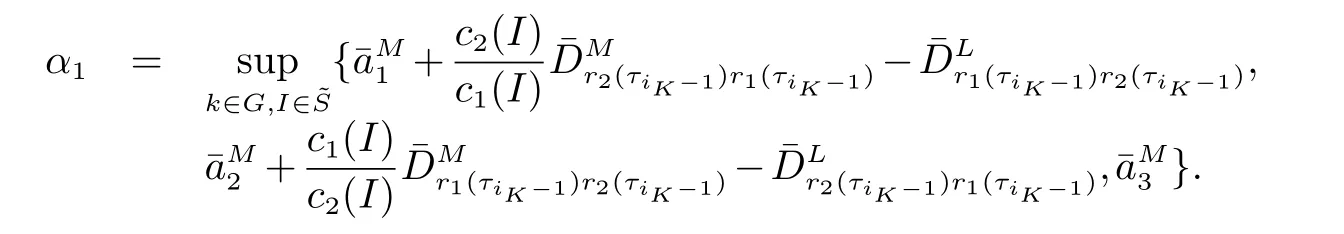
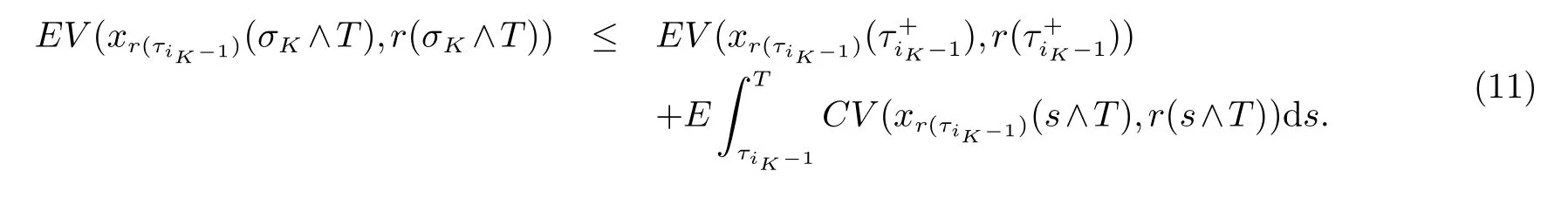
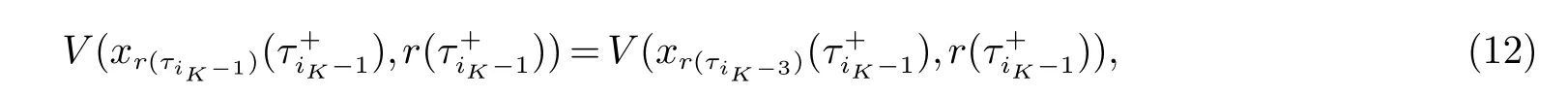
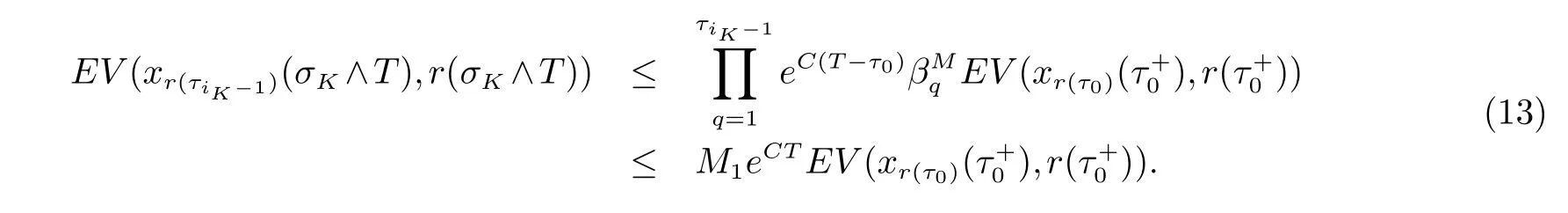
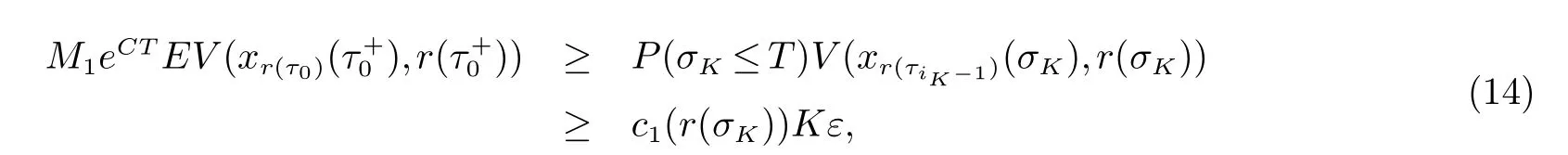
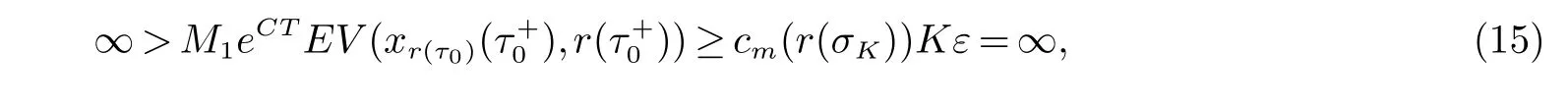

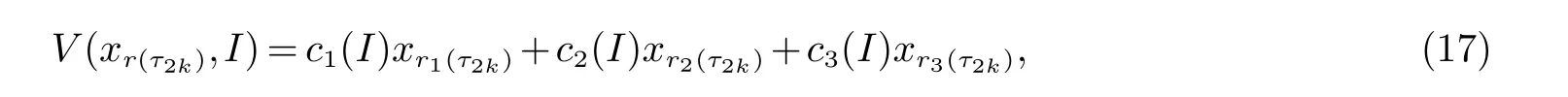
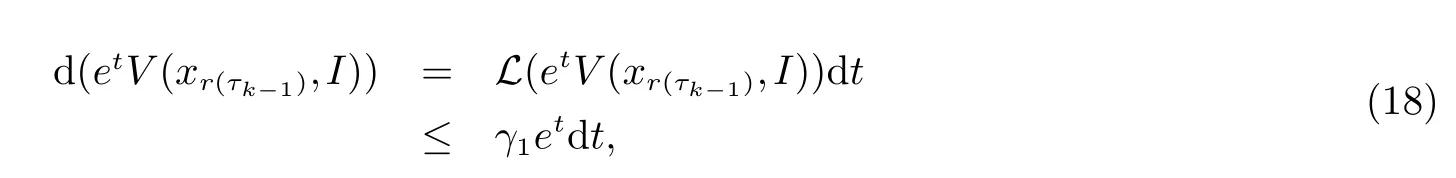
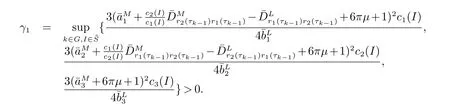
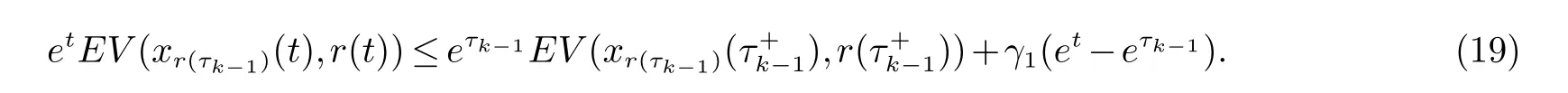
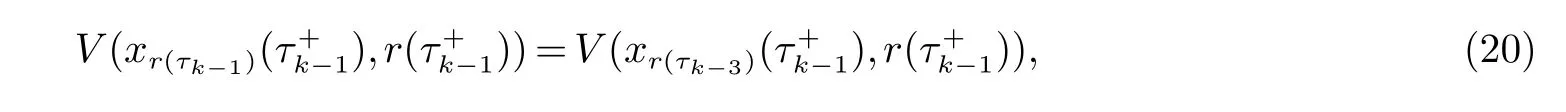

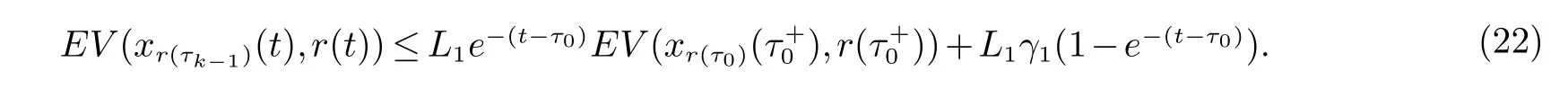
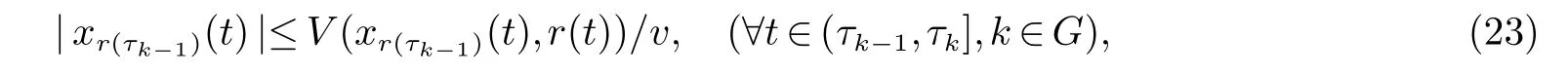
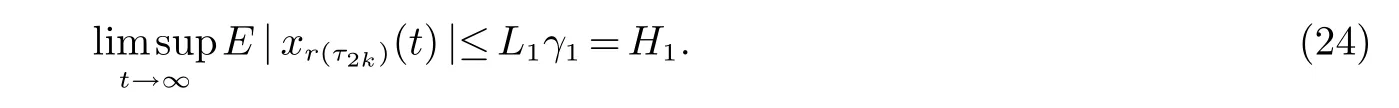
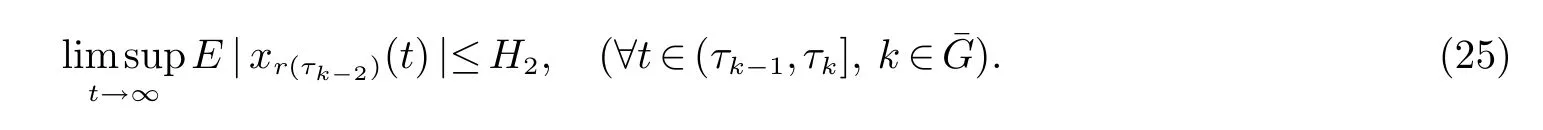

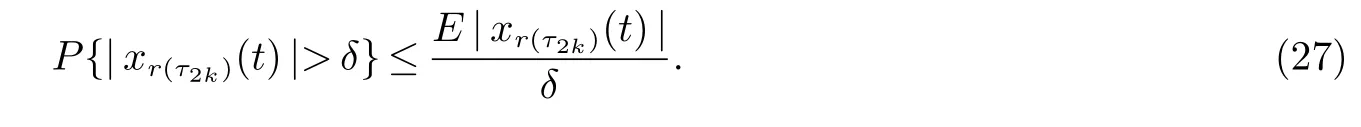

- 新疆大学学报(自然科学版)(中英文)的其它文章
- The Absolute Ruin Risk Model with Constant Interest Investment and Linear Threshold Dividend Strategy∗
- 煤基活性炭的氧化改性及其对Cd2+的吸附性能∗
- 细菌诱导光滑鳖甲幼虫抑制差减cDNA文库的构建与分析∗
- 资源型产业与制造业集聚特征与影响因素异同分析∗
- Distance Signless Laplacian Integral Complete R-partite Graphs∗
- Finite-time Stability of Continuous-time Systems with Time-varying Delays∗

