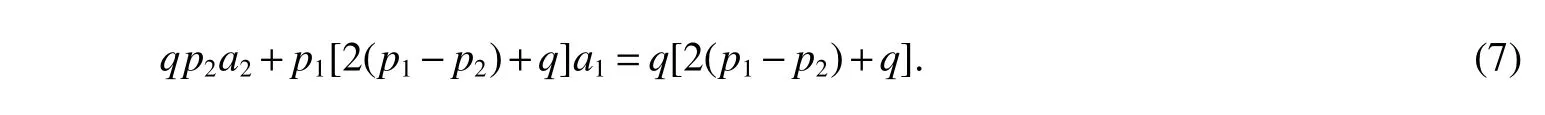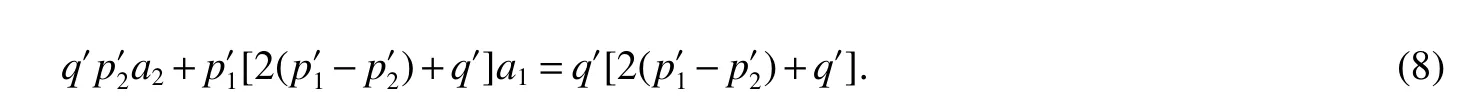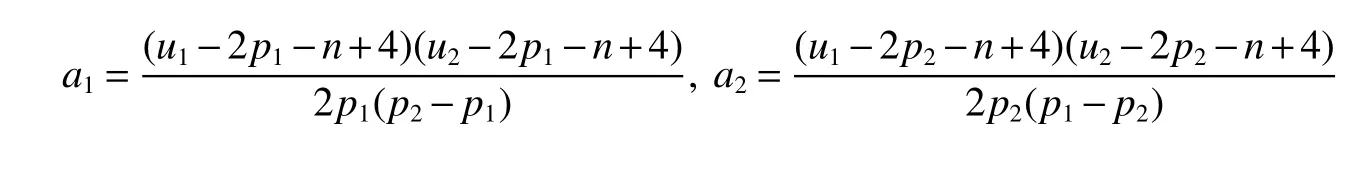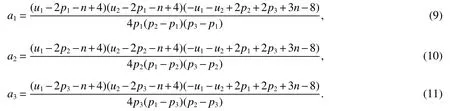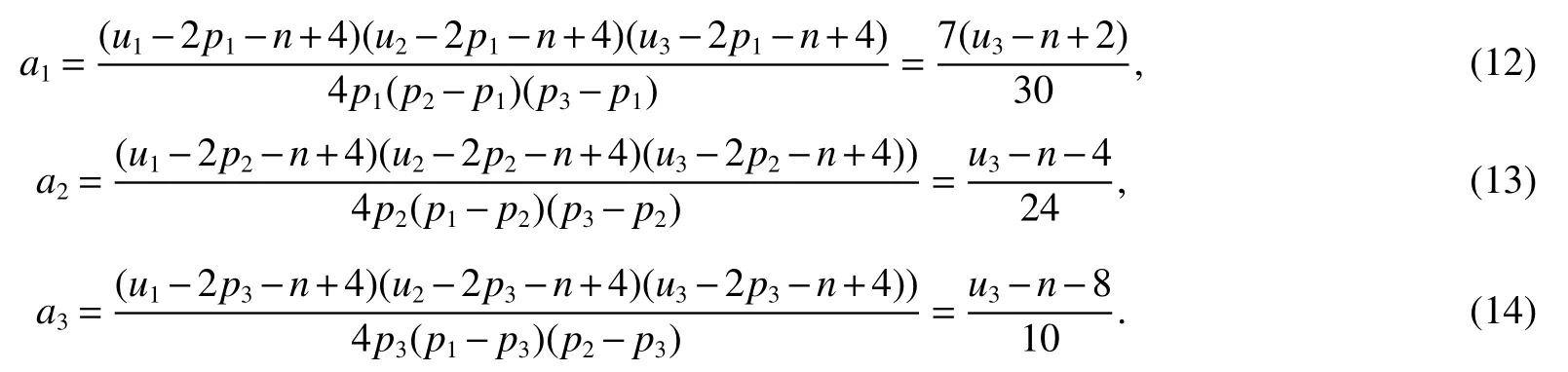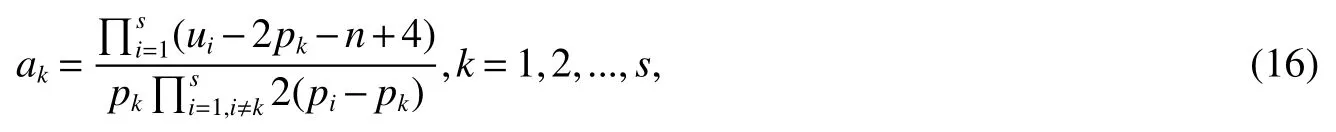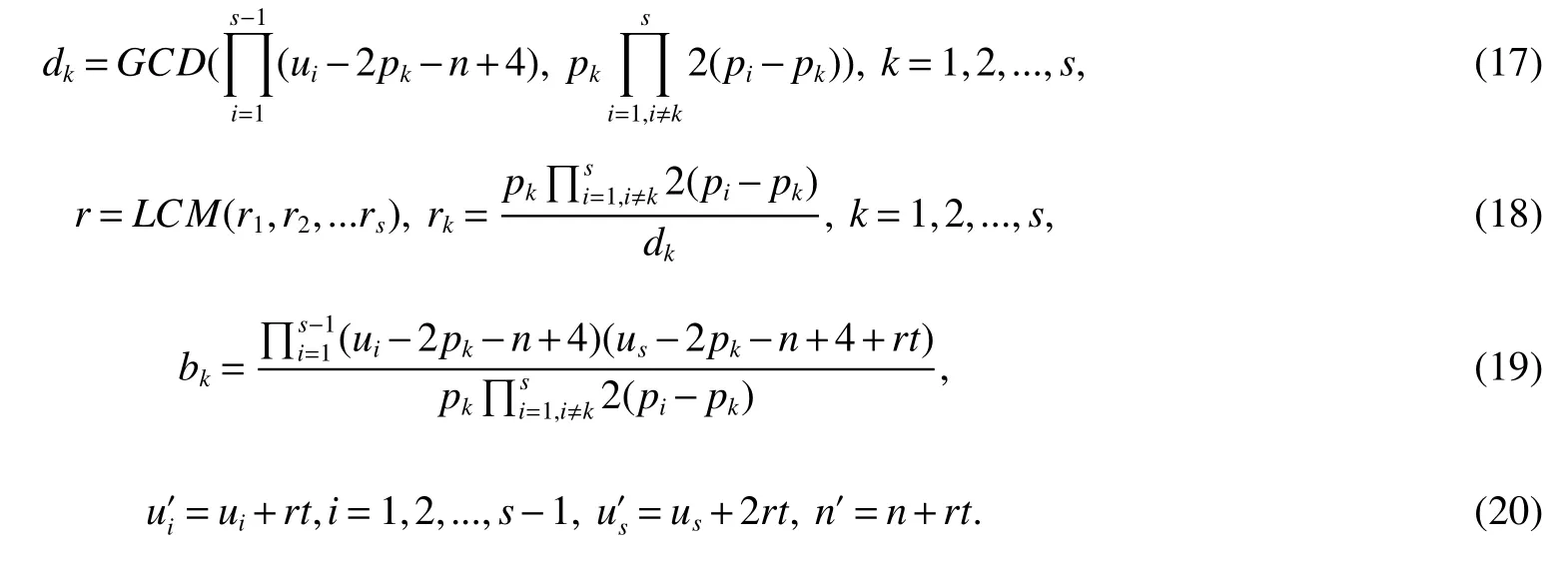Distance Signless Laplacian Integral Complete R-partite Graphs∗
ZHAO Shuang,LI Dan,MENG Jixiang
(College of Mathematics and System Sciences,Xinjiang University,Urumqi Xinjiang 830046,China)
0 Introduction
All graphs considered in this paper are simple,connected and undirected.LetG=(V,E)be a simple graph with vertex setV(G)={v1,v2,...vn},edge setE(G)and letn=|V(G)|ande(G)=|E(G)|denote its order and size,respectively.The neighbor set and the degree of the vertexviare denoted byN(vi)anddi=|N(vi)|,respectively.The adjacency matrix of G,A(G)=(aij)n×nis a(0,1)-matrix,whereaij=1 ifvivj∈E(G)andaij=0 otherwise.The characteristic polynomial|λIn−A(G)|,whereInis then×nidentity matrix,is called the characteristic polynomial of G.A graph G is called integral if all the zeros of the characteristic polynomial are integers.Let 4(G)=diag(d1,...,dn)be the diagonal degree matrix.The signless Laplacian matrix of G is defined asQ(G)=4(G)+A(G).The eigenvalues ofQ(G)are called the signless Laplacian eigenvalues(or simply Q-eigenvalues).If all Q-eigenvalues of a graph G are integers,we call G Q-integral.
LetdG(u,v)denotesthedistancebetweenverticesuandv,andletD(G)=(dij)n×nbethedistancematrixofG,wheredij=dG(vi,vj).The vertex transmission ofviis defined to be the sum of the distances fromvito all other vertices in G,and is denoted byDvi(G),or simplyDi,that is,Di=Pnj=1dij.LetTr(G)=diag(D1,...,Dn)denotes the diagonal matrix of its vertex transmission.The distance signless Laplacian matrix of a graph G is defined asDQ(G)=Tr(G)+D(G).The distance signless Laplacian characteristic polynomial(orDQ-polynomial)of G isDQG(λ)=|λIn−DQ(G)|,whereInis then×nidentity matrix.The eigenvalues ofDQ(G),called distance signless Laplacian eigenvalues of G,are labeled asu1≥u2≥...≥un.Assume thatu1>u2>...>utare t distinctDQ-eigenvalues of G with the corresponding multiplicitiesk1,k2,...,kt.We denote byspec(G)=the distance signless Laplacian spectrum or theDQ-spectrum of G.Similar to the above definition of integral and Q-integral,we can define distance signless Laplacian integral.A graph is said to be distance signless Laplacian integral if all itsDQ-eigenvalues are integers.
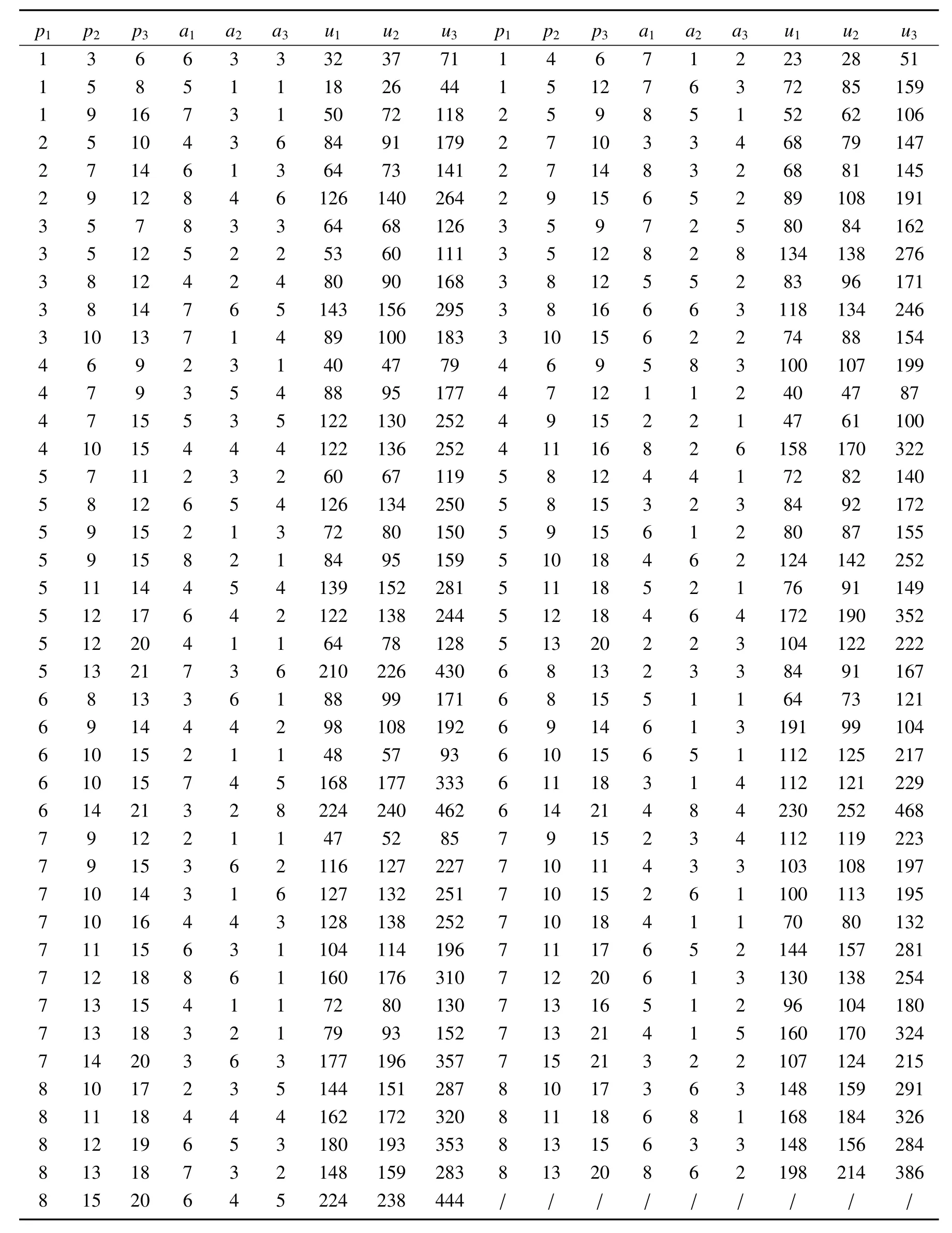
LetKp1,p2,...,prbe the complete r-partite(r≥2)graph.Assume that there are s different integers inp1,p2,...,prand assume,without loss of generality,p1 Wang et al.[1]gave a useful necessary and sufficient condition for complete r-partite graphs to be integral,from which they constructed infinitely many new classes of integral graphs.Then Wang and Liu investigated integral complete r-partite graphsKp1,p2,...,pr=Ka1·p1,a2·p2,...,as·pswiths=3,4[2].The author gave some sufficient conditions for complete 3-partite graphs to be integral[3].H´ıc and Pokorn´y[4]constructed the first known integral complete 4-partite graphKp1,p2,p3,p4,wherep1 The remaining part of this paper is organized as follows.In the next section,we give a necessary and sufficient condition for the graphsKp1,p2,...,pr=Ka1·p1,a2·p2,...,as·psto be distance signless Laplacian integral.In the last part,we construct infinitely many new classes of distance signless Laplacian integral graphs. In what follows we shall give a necessary and sufficient condition for complete r-partite graphs to be distance signless Laplacian integral. LetIpkdenotes thepk×pkidentity matrix fork=1,2,...,randJpi×pjdenotes thepi×pjmatrix with all entries equal to 1,fori,j=1,2,...,r.Especially,ifpi=pj,we useJpkfor simplicity. Theorem 1LetG=Kp1,p2,...,prbe the complete r-partite graph with ordern=Pri=1pi,then ProofBy properly ordering the vertices of G,we can derive its distance signless Laplacian matrixDQ(G)such that theDQ(G)-polynomial is given by whereBk=(λ−n−pk+4)Ipk−2Jpk,fork=1,2,...,r.Then the result easily follows. Corollary 1Let G be a complete r-partite graphKp1,p2,...,pr=Ka1·p1,a2·p2,...,as·pson n vertices.Then theDQ-polynomial of G is ProofIt is not difficult to obtain the result from Theorem 1. The following result can be easily obtained from Corollary 1. Corollary 2Let G be a complete r-partite graphKp1,p2,...,pr=Ka1·p1,a2·p2,...,as·pson n vertices.We have the following results (i)ifs=1,thenKp1,p1,...,p1=Ka1·p1is distance signless Laplacian integral,where its distance signless Laplacian spectrum is (ii)ifs=2,a1=a2=1,thenKp1,p2is distance signless Laplacian integral if and only ifis a perfect square. From Corollary 1,we can obtain the following result. Theorem 2The complete r-partite graphKp1,p2,...,pr=Ka1·p1,a2·p2,...,as·psof order n is distance signless Laplacian integral if and only if has only integral roots. In order to get more information,now we discuss Eq.(1).At first,we divide both sides of Eq.(1)byn+4),and obtain LetF(x)=1−Clearly,for 1≤i≤s,xi=(2pi+n−4)’s are not roots of Eq.(1).So we can conclude that Eq.(1)and Eq.(2)have the same solutions.Now we consider the roots of F(x)over the set of real numbers.Note that F(x)is discontinuous at each point 2pi+n−4.For 1≤i≤s,we can obtain thatF((2pi+n−4)−0)=+∞,F((2pi+n−4)+0)=−∞,F(−∞)=F(+∞)=1,F'(x)=Thus F(x)is strictly monotone increasing on each of the continuous intervals over the set of real numbers.Owing to the Bolzano’s Theorem or the Weierstrass Intermediate Value Theorem of Analysis,we acquire that F(x)has s distinct real roots.Let−∞ holds. On the other hand,we note that Eq.(2)can be written as By the above discussion,we can easily obtain the following theorem. Theorem 3The complete r-partite graphKp1,p2,...,pr=Ka1·p1,a2·p2,...,as·psof order n is distance signless Laplacian integral if and only if all the solutions of Eq.(4)are non-negative integers.Moreover,the graphKp1,p2,...,pr=Ka1·p1,a2·p2,...,as·psis distance signless Laplacian integral if and only if there exist integersu1,u2,...,ussatisfying(3)such that the following linear equation system ina1,a2,...,as has positive integral solutions(a1,a2,...,as). Theorem 4If the complete r-partite graphKp1,p2,...,pr=Ka1·p1,a2·p2,...,as·psof order n is distance signless Laplacian integral,then there exist integersui(i=1,2,...,s)such that−∞<2p1+n−4 Conversely,suppose that there exist integersui(i=1,2,...,s)such that−∞<2p1+n−4 ProofWe cite Cauchy’s result on determinants from[9] Let D be the coefficient matrix of(5).Then To solve the linear equation system in(a1,a2,...,as),we use the famous Cramer’s Rule and get that Sinceuiandaiare integers,−∞<2p1+n−4 On the other hand,ifaiare positive integers anduiare integers,the remaining part of the theorem is obvious. Corollary 3If the complete r-partite graphKp1,p2,...,pr=Ka1·p1,a2·p2,...,as·psof order n is distance signless Laplacian integral with non-negative integral eigenvaluesui(i=1,2,...,s),whereui(i=1,2,...,s)are those of theorem 4,then we have (i) (ii) (iii)spec(Ka1·p1,a2·p2,...,as·ps)= ProofBy Corollary 1,we have Then the results can be obtained easily by using the relationship between roots and coefficients of polynomials. To fi nd out the relationship between the distance signless Laplacian integral complete r-partite graphsKp1,p2,...,pr==(a1,a2,...,as),.,ps)∈We define=and(x)=(x−2pi−n+4)(1−),wheren=Thus we have the following lemma. lemma 1Let q be a nonzero integer.Then u is an integral root ofif and only if[(u+4−n)/q]+(n−4)is an integer root of ProofIt is easy to see that v is a root ofif and only ifq(v+4−n)+(n−4)is a root ofso if all the roots ofare integers,the roots ofare also integers. Suppose that all roots ofare integers and that u is one of them,then[(u+4−n)/q]+(n−4)is a rational root ofSinceis a monic polynomial with integral coefficients,its rational roots should be integers.So,[(u+4−n)/q]+(n−4)∈Z. From the above lemma we can get the following result. Corollary 4The complete r-partite graphKp1q,p2q,...,prq=Ka1·p1q,a2·p2q,...,as·psqis distance signless Laplacian integral for any positive integer q if and only if the complete r-partite graphKp1,p2,...,pr=Ka1·p1,a2·p2,...,as·psis distance signless Laplacian integral. Remark 1Call a vector(p1,p2,...,ps)primitive ifGCD(p1,p2,...,ps)=1,whereGCD(p1,p2,...,ps)denotes the greatest common divisor of the numbersp1,p2,...,ps.So,in general,Corollary 4 shows that the primitive vectors are the only ones that we are interested in. In this section,we are to construct infinitely many new classes of distance signless Laplacian integral complete r-partite graphsKp1,p2,...,pr=Ka1·p1,a2·p2,...,as·pswiths=2,3. In order to construct such distance signless Laplacian integral complete r-partite graphs,our main idea is following:firstly,choose positive integersp1,p2,...,psproperly.Secondly,try to find integersui(i=1,2,...,s)satisfying(3)such that either there are positive integral solutions(a1,a2,...,as)for(5)or allak’s of Eq.(6)are positive integers.And fi nally,obtain positive integers(a1,a2,...,as)such that all solutions of Eq.(4)are integers. Theorem 5Fors=2,letp1 (i)GCD(p1,p2)=1.Letu1=2p1+n−4+q,and q be a positive integer with 1≤q<2(p2−p1).Then,a1anda2must be positive integral solutions for the Diophantine equation Furthermore,there are in fi nitely many integral solutions(a1,a2)for Eq.(7). (ii)GCD(p1,p2)=d≥2.Letp1=2p1+n−4+q,q=q'd,1≤q'<2(p'2−p'1).Then,a1anda2must be positive integral solutions for the Diophantine equation Furthermore,there are infinitely many integral solutions(a1,a2)for Eq.(8). ProofOn account ofp1 Substitutingu1by 2p1+n−4+q,we deducea1=and Eq.(7)is then established. From elementary number theory,we know that there are solutions for Eq.(7)if and only ifd1|q[2(p1−p2)+q],whered1=GCD(qp2,p1[2(p1−p2)+q]). Now,we discuss two cases. Case 1GCD(p1,p2)=1.Thend1|q[2(p1−p2)+q],and further,there are solutions for Eq.(7).From elementary number theory and conditionGCD(p1,p2)=1,we know that there are infinitely many integral solutions(a1,a2)for Eq.(7). Case 2GCD(p1,p2)=d≥2.Thend1=GCD(qp2,p1[2(p1−p2)+q])=Ifd1|q[2(p1−p2)+q]=thend|q.We can reduce(7)to(8).Hence,from elementary number theory and the condition=1,we know that there are infinitely many integral solutions(a1,a2)for Eq.(8). Theorem 6Fors=3,integerspi,aiandui(i=1,2,3)are given in Table 1.pi,ai,andui(i=1,2,3)are those of theorem 4,whereGCD(p1,p2,p3)=1.Then for any positive integer q,the graphKa1·p1q,a2·p2q,a3·p3qof order n is distance signless Laplacian integral. ProofFrom Theorem 4,Ka1·p1,a2·p2,...,as·psof order n is distance signless Laplacian integral if and only if there exist integersui(i=1,2,...,s)such that(3)holds andak=(k=1,2,...,s)are positive integers. By(i)of Corollary 3,we have+n,and thenu3=−u1−u2+wheren=From Corollary 4,it is only necessary to considerGCD(p1,p2,...,ps)=1.Hence,whens=3,it is sufficient to find only all positive integerspi,ai(i=1,2,3),u1,u2andu3for the following equations: By using a computer search,we have found 190 integral solutions satisfyingGCD(p1,p2,p3)=1 for(9),(10),and(11),where 1≤p1≤10,p1+1≤p2≤p1+10,p2+1≤p3≤p2+10,1≤ai≤10,(i=1,2,3),2p1+n−4 Theorem 7Fors=3,letpi,aiandui(i=1,2,3)be those of Theorem 4.Then for any positive integer q,the graphsKa1·p1q,a2·p2q,a3·p3qof order n are distance signless Laplacian integral ifp1=1,p2=4,p3=6,u1=n,u2=n+5,andu3=120t+n+28,a1=28t+7,a2=5t+1,anda3=12t+2,wheren==120t+23 and t is a positive integer. ProofFors=3,from Table 1,we choosep1=1,p2=4,p3=6.Thenu1=n,u2=n+5.By Theorem 4,we deduce Thus,Ka1·p1,a2·p2,a3·p3is distance signless Laplacian integral if and only ifa1,a2,a3are positive integers,andu3must be a positive integer.From(13)and(14),we get the Diophantine equation Table 1 Distance signless Laplacian integral complete r-partite graphs Ka1·p1,a2·p2,a3·p3 A result in elementary number theory yields that all positive integral solutions of Eq.(15)are given byu3=120t+n+28,a2=5t+1,anda3=12t+2,where t is a positive integer.By the above discussion and(12),we havea1=28t+7. Therefore,ifp1=1,p2=4,p3=6,thenu1=n,u2=n+5,andu3=120t+n+28,a1=28t+7,a2=5t+1,anda3=12t+2,the complete r-partite graphKa1·p1,a2·p2,a3·p3is distance signless Laplacian integral,wheren=P3i=1aipi=120t+23 and t is a positive integer.From Corollary 4,for any positive integer q,the graphKa1·p1q,a2·p2q,a3·p3qis distance signless Laplacian integral. Remark 2Analogously to Theorem 7 it is possible to find conditions for parametersu3,ai(i=1,2,3)which depend on t for the corresponding graphKa1·p1,a2·p2,a3·p3,wherepi,ai(i=1,2,3)are those of Table 1.By this procedure new classes of distance signless Laplacian integral graphs can be obtained. Remark 3Suppose thatp1 Similar results with the following theorem for complete multipartite graphs were given in[10].This is another way of constructing infinitely many new classes of distance signless Laplacian integral complete r-partite graphs.LetLCM(r1,r2,...rs)denotes the lowest common multiple of the numbersr1,r2,...rs. Theorem8Letthecompleter'-partitegraphKp1,p2,...,pr'=Ka1·p1,a2·p2,...,as·psofordern=bedistancesignless Laplacian integral with eigenvaluesui,whereuiandpi(i=1,2,...,s)be integers such that−∞<2p1+n−4 are positive integers.Let t be any positive integer.Then the completer''-partite graphKp1,p2,...,pr''=Kb1·p1,b2·p2,...,bs·psonn'vertices is distance signless Laplacian integral with non-zero distance signless Laplacian eigenvaluesfor ProofUsing(16-20)we have,fork=1,2,...,s, It follows from(18)that,bk(k=1,2,...,s)are positive integers for every positive integer t.Since−∞<2p1+n−4 References: [1]Wang L G,Li X L,Hoede C.Integral complete r-partite graphs[J].Discrete Math,2004,283:231-241. [2]Wang L G,Liu X D.Integral complete multiparite graphs[J].Discrete Math,2008,308:3860-3870. [3]H´ıc P,Pokorn´y M,ˇCernek P.New sufficient condition for integral complent 3-partite graphs[J].Appl Anal Discrete Math,2008,2:276-284. [4]H´ıc P,Pokorn´y M.Integral complete 4-partite graphs[J].Discrete Math,2008,308:3704-3705. [5]Wang L G,Wang Q.Integral complete multiparite graphsKa1·p1,a2·p2,...,as·pswiths=5,6[J].Discrete Math,2010,310:812-818. [6]Zhao G P,Wang L G,Li K.Q-integral complete r-partite graphs[J].Linear Algebra Appl,2013,438:1067-1077. [7]Yang R S,Wang L G.Distance integral complete r-partite graphs[J].Filomat,2015,29(4):739-749. [8]Pokorn´y M,H´ıc P,Stevanovi´c D.Remarks on Q-integral complete multipartitie graphs[J].Linear Algebra Appl,2013,439:2029-2037. [9]Borwein P,Erd´elyi T.Polynominals and Polynominal Inequalities[M].New York,Berlin,Heidelberg:Speringer,1995,106-107. [10]H´ıc P,Pokorn´y M.New classes of integral complete n-partite graphs[J].Advances and Applications in Discrete Mathematics,2011,7(2):83-94.1 A necessary and sufficient condition for complete r-partite graphs to be distance signless Laplacian integral
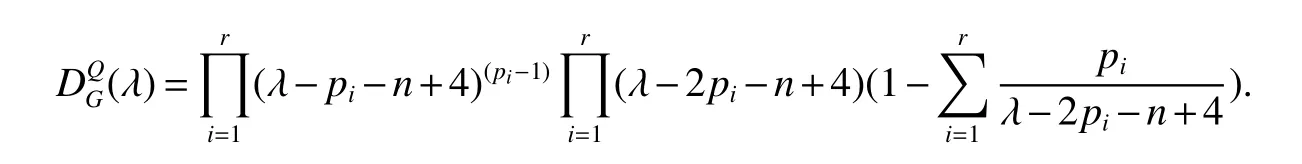
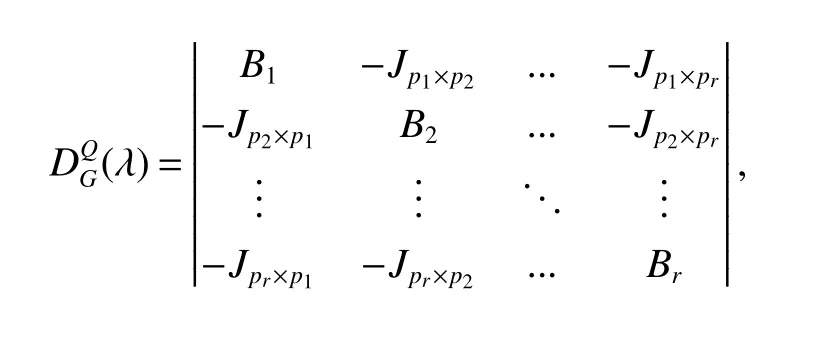
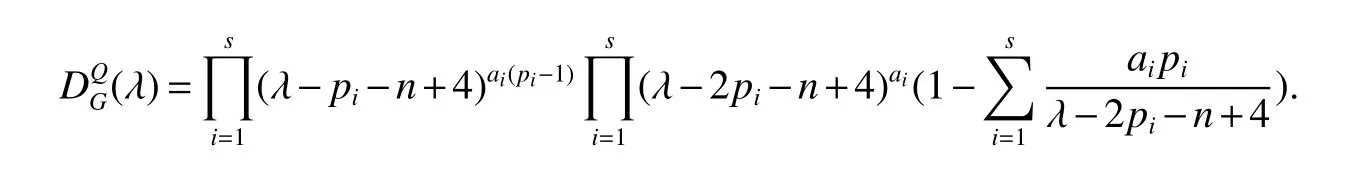
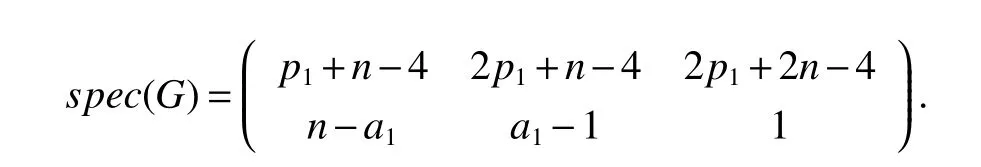
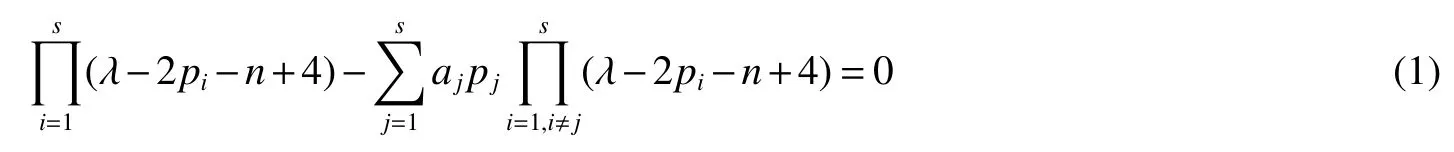

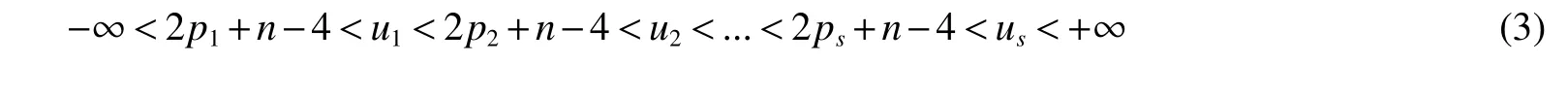
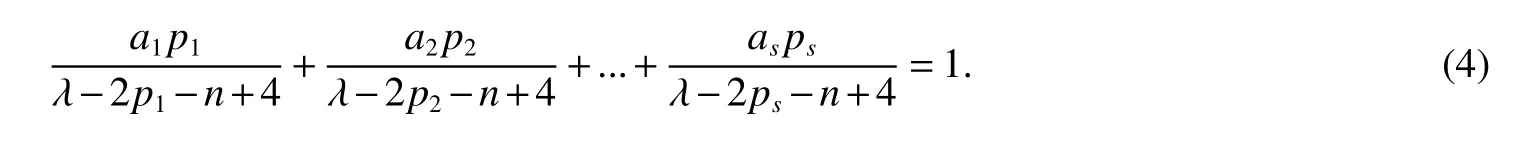
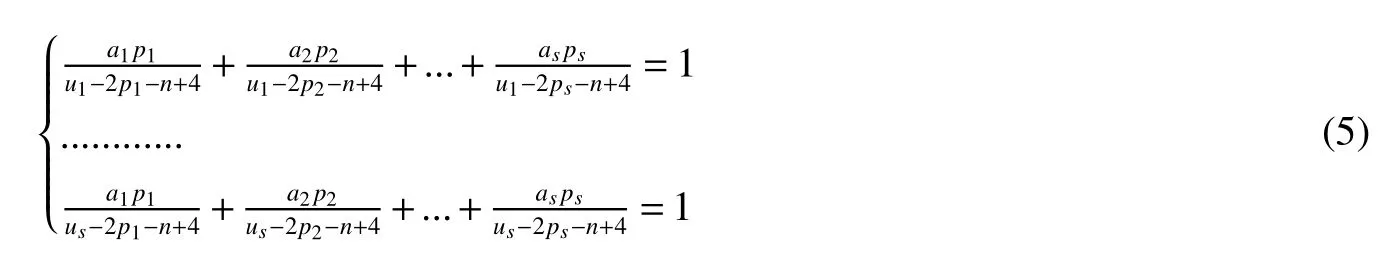
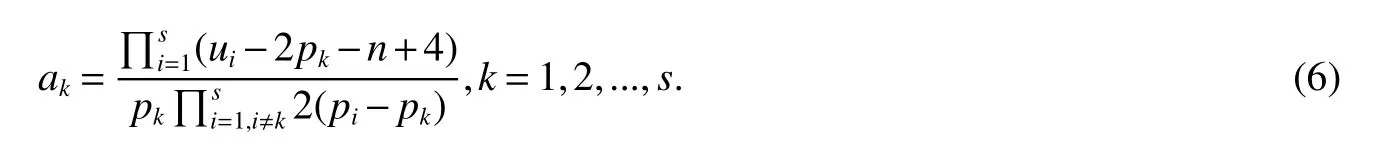
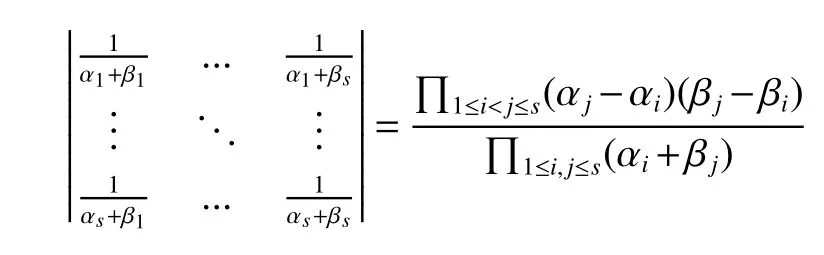

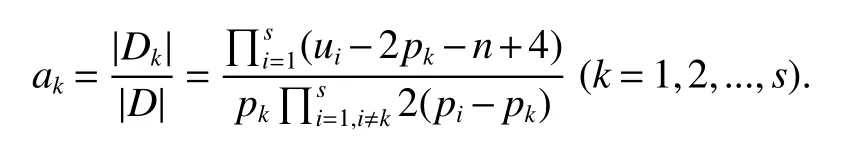
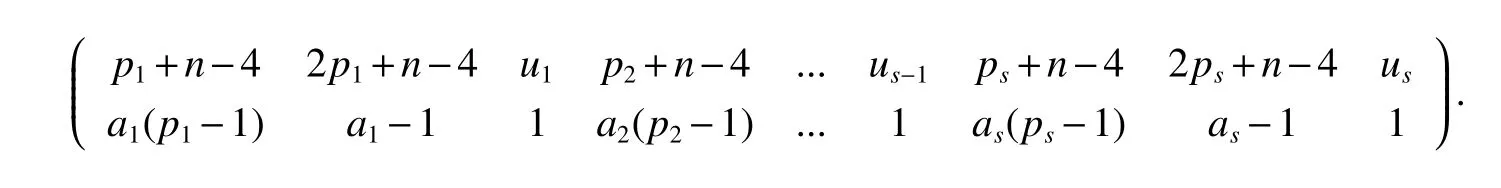
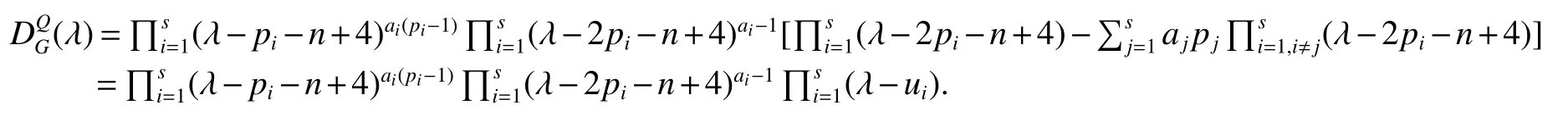
2 Distance signless Laplacian integral complete r-partite graphs