联通度量本质 形成量角技能

林宏滨

在日常教学中，技能教学的主要形式往往是教师讲解、示范、演示操作，以及学生模仿并进行强化联系的过程。此过程学生处于机械接受模仿状态，缺乏自主思考和探究的空间，从而造成学习效果低下。其实，不管是概念教学还是技能教学，都要让学生挖掘知识技能背后所蕴含的知识本质，经历自主探究知识的过程，方能培养学生的独立思考及创新能力。

一、困惑———学生为什么不会量角

如果你问学生：“用量角器怎么量角？”学生会不假思索地告诉你：“把角的顶点和量角器的中心重合，一条边和0度刻度线重合，看另一条边所对应的刻度就可以了。”可当学生拿起量角器量角，他们却不知道如何摆放，更谈不上解决稍微复杂的量角问题。如果再追问学生：“量角器是怎么来的？”“为什么用量角器可以量角？”学生则表现出一脸困惑。从这里可以看出学生根本就不明白“量角”的本质，所以技能操作就存在困难。量角“二合一看”等口诀，对学生来说就是一个背诵下来的句子，而并非是真正意义上对量角技能的理解，对学生真正掌握量角方法并不能起到有效的辅助作用。

二、思考———找准度量本质再操作

角的度量，其知识本源就是度量，度量是将事物的属性量化，赋予事物一个“数”，从而可以在同一纬度上比较事物。“角”作为新的度量对象，虽然与长度、面积等有着明显的不同，但其度量本质是相同的，都是要先确定度量单位，然后再测量出被度量的物体里含有多少个这样的基本度量单位，也就是一个具体的“数”。为此，在教学中要沟通学生已有测量长度、面积的方法与角的度量之间的联系，联通度量知识的本质，把单调、乏味的技能教学变成丰富、厚重且充满思考的课堂，让学生在感悟数学本质的过程中掌握技能，从而使“角的度量”一课的教学目标更丰厚一些。如果我们抓住本质进行教学，那结果就不一样了。

【教学环节1】联通已知，产生度量单位。

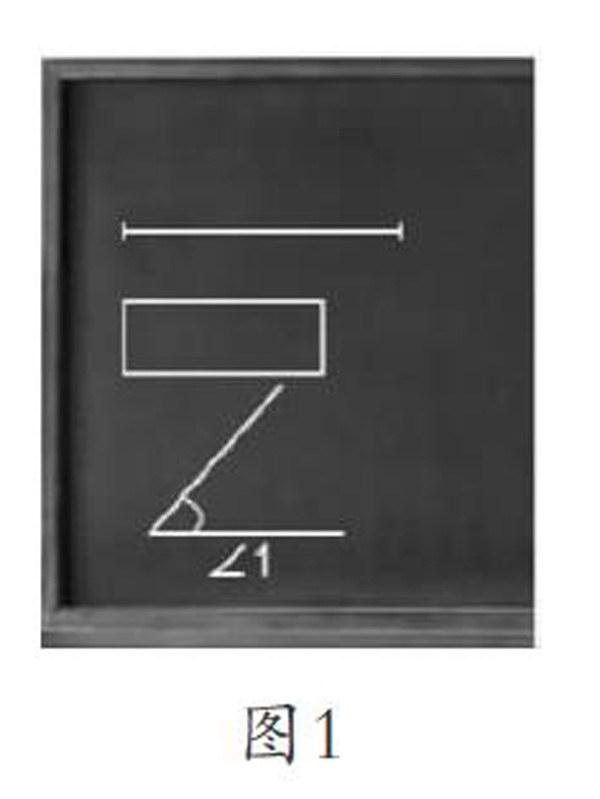
教师在黑板上画一条线段（4 dm）、一个长方形（长3 dm，宽1 dm）、一个角（∠1=50°）（如图1）。

①引导学生用1 dm的小尺子量黑板上线段的长度，量了4次，感悟4个1 dm即4 dm。

②用面积是1 dm2的小正方形量黑板上长方形的面积，量了3次，感悟3个1 dm2即3 dm2。

③设疑：今天咱们要度量∠1的大小，也得知道什么？（角的度量单位）

④用长度单位或面积单位来度量角可好？为什么？学生在交流中感悟角的大小与边的长短无关，所以不可用长度单位来度量；角不是封闭图形，所以不能用面积单位来度量角的大小，从而产生角的度量单位。

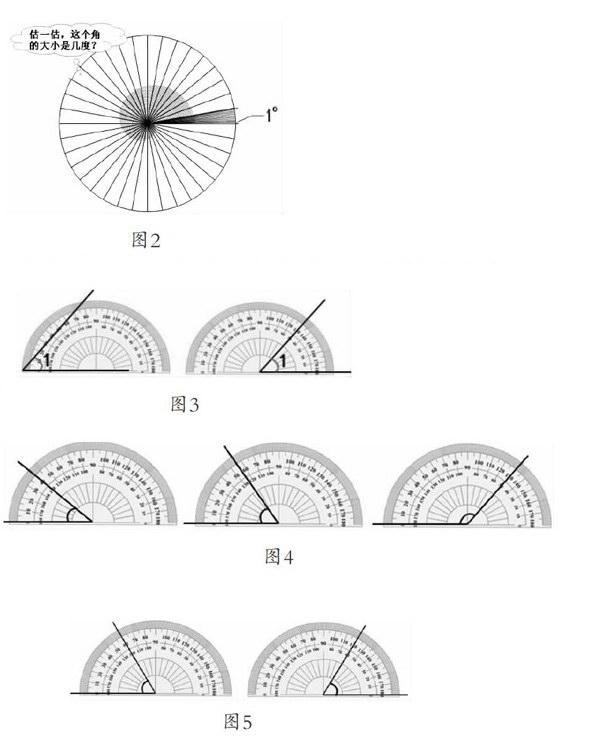
⑤让学生比划1°长什么样？初步感知角的度量单位是一个角，进而猜想多大的小角是1°？并用视频介绍1°的由来，以及把圆等分360份得到1°角。

度量角和度量长度、度量面积都是一样的，要先确定一个度量标准，也就是度量单位。那角的度量单位应该是什么形状？让学生自己去说理发现：角的度量单位不能是一条线段，因为角的大小与边的长短无关；也不能是一个正方形，因为角不是封闭图形。从而得出：度量角的单位也得是一个角，而且必须是一个很小的角，不然就无法准确度量出角的度数了。学生在讲理沟通中，明白度量单位1°产生的道理，让知识的产生有理有据。

【教学环节2】估角活动，感悟度量本质。

当学生认识了“1°”这一角的度量单位后，为了更有效地沟通角的度量本质，让学生感悟无论是度量线段、度量面积还是度量角，其本质都是一样的，即“看要度量的物体含有几个这样的度量单位即几度”。笔者创设了如下教学环节。

①创设估角环节，让学生估5°角，在交流估角方法的同时感悟估角其实就是看要估的角含有几个1°小角。

②在36等分圆中估10°角（如图2），初步建构10°角的模型。

③借助10°角这一模型估30°角和黑板上的∠1，进一步感悟要知道角有多大？需要知道它包含有几个这样的度量单位。

“估角”其实是利用度量的本源去思考如何量角，就是看这个角里含有几个1°角或者几个10°角，这是量角方法的雏形，同时也让学生在量角之前就对这个角的度数范围有一个比较合理的预测，建立角的大小的空间观念，初步感受量角这一技能背后所蕴含的知识本质，为后续量角做好铺垫。

【教学环节3】探究交流，形成量角技能。

联通了线段、面积、角等度量知识本质后，学生产生了知道黑板上∠1的大小的渴望。为了提炼量角方法，形成量角技能，笔者创设如下的教学环节，让学生从尝试量角、产生困惑、对比说理、沟通方法、找角读角的过程中形成量角技能。

①初识工具。学生观察手中的量角器，在四人小组中交流自己对量角器已有的生活认知。

②尝试量角。学生尝试用量角器量∠1，教师收集学生初次使用量角器的困惑，并展示学生的两种量角方法（如图3）。

③对比说理。引导学生对比两种量角方法的不同，追问：“这两种量法谁对谁错，为什么？”引导学生在交流中感悟要判断哪种量法是正确的，得看哪种量法能在量角器上看出∠1含有几个10°角。

④沟通方法。组织学生数出正确量法中的∠1含有5个10°角，即∠1=50°。追问：“怎样摆才能让我们在量角器中看出∠1含有5个10°角？”

⑤找角读角。教师依次摆出40°、65°、135°角（如图4），组织学生在找角读角的过程中，感悟度量角的本质，即被度量的物体里含有多少个这样的基本度量单位。再通过读正向和反向的60度（如图5），形成读角技能。

⑥自主度量。最后，笔者让学生再次量∠1，在第2次量角操作中提炼量角方法。

从“头”量起，是学生已有度量认知的思维定势，角的度量并非从“头”量起，所以学生学习起来是有难度的。本环节立足学生的错误资源，进行对比，让学生通过说理辨析，于度量本质中感悟量角方法。同时，通过看量角器的角、读角的度数，让学生把握量角器上的角与要度量的角之间的重合关系，突破量角的难点，形成量角技能。

三、感悟———溯本方能悟其真知

1. 沟通本源唤醒度量经验。

角的度量其知识本源就是度量，虽与度量长度、度量面积等有着明显的不同，但其本质都是一样的。教学中教师不仅要善于沟通学生已有度量长度、面积的方法与角的度量之间的联系，唤醒其已有的度量经验，更重要的是将其本质进行联通，即“都要先有角的度量单位才能进行度量，都要看被度量的物体里含有多少个基本度量单位”。这样，才能让学生立足已有度量的经验，掌握并形成度量技能。

2. 经历过程把握度量本质。

很多教师在技能教学中，为了节省时间，便把如何操作直接告知学生，而忽略了让学生体验技能的形成过程。“学生是教不会的”，学生对数学知识的理解，依赖的不是教师的讲解与灌输，而是参与教学活动中自己所收获的思考和感悟。学生在估角活动中，明白度量角的大小就是看这个角含有几个1°角；在自主量角中，通过对错误的对比、辨析，提炼量角的方法，把握度量的本质；最后在找角、读角过程中，领悟并把握角的度量本质。这样的亲历体验，学生掌握的不仅仅是知识技能，而是在理解知识的本质中感悟数学基本思想，积累数学活动经验。

3. 明白道理形成度量技能。

这节课，学生只度量了4个角，但课后学生的量角准确率极高，这一成效说明了一个问题，技能的形成并不一定需要反复地操作。学生为什么不会量角，就是因为他们不知道量角器这一工具和角之间的关系，不明白“角的顶点和量角器的中心重合，一条边和0度刻度线重合，看另一条边所对应的刻度”这一操作背后的道理，当学生明白了量角就是要看这个角包含几个10°角或者几个1°角后，就会明白，重合的目的就是要在量角器上找到和所要度量的这个角大小相等的角，这样就可以得出角的度数。学生明白操作的道理后，量角技能的形成也就水到渠成了。

（作者单位：福建省厦门市海沧区新江中心小学）