从模糊集到直觉模糊集相似度的构造方法

刘鹏惠

(西华大学理学院，四川 成都 610039)



从模糊集到直觉模糊集相似度的构造方法

刘鹏惠

(西华大学理学院，四川 成都 610039)

摘要：直觉模糊集的相似度是直觉模糊集的一个重要研究内容。从模糊集相似度角度，提出直觉模糊集相似度的一些构造方法。基于模糊集的相似度得到直觉模糊集的隶属度与非隶属度的相似度，进而提出从模糊集相似度构造直觉模糊集相似度的方法；利用已有的模糊集相似度公式，得到了17个新的直觉模糊集相似度；通过一个例子演示新相似度在模式识别方面的应用。

关键词：模糊集；直觉模糊集；相似度

Atanassov提出的直觉模糊集[1-2]是Zadeh提出的模糊集[3]的一种推广形式。Bustince 等[4]指出Gau等提出的含糊集[5]等同于直觉模糊集。一个直觉模糊集由隶属度、非隶属度2个参数来描述，因此，直觉模糊集比模糊集在处理不确定性方面更具灵活性和实用性。目前直觉模糊集已广泛应用于模式识别、决策分析、机器学习等领域。

直觉模糊集之间的相似性度量是直觉模糊集理论的一个重要研究内容，受到国内外学者的极大关注。目前，人们已从不同角度提出了许多直觉模糊集相似度计算公式[6-14]，这些相似度大多是基于距离的拓展。本文主要是从模糊集相似度的角度研究直觉模糊集相似度的一些构造方法。直觉模糊集的隶属度与非隶属度可以看成是论上的2个模糊集，因此可以利用模糊集的相似度公式来度量直觉模糊集的隶属度与非隶属度的相似性，从而通过线性组合得到直觉模糊集的相似度计算公式。

1预备知识

为便于讨论，下面介绍模糊集相似度与直觉模糊集相似度的基本概念。

1.1模糊集与模糊集的相似度

定义1[3]设X为一非空论域，X上的一个模糊集A是论域X到[0,1]的一个映射：

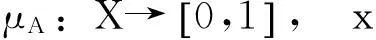
其中μA(x)称为元素x属于模糊集A的隶属度，即X上的模糊集是一个二元组：

一般地，x属于模糊集A的隶属度，简记为A(x)，X上的全体模糊集记为F(X)。X上的模糊集有如下一些基本运算：

1)A⊆B⟺∀x∈X, A(x)≤B(x)；

2)A=B⟺ A⊆B并且B⊆A；

3)A的补集Ac定义为 Ac(x)=1-A(x)；

4) 模糊集A与B的并A∪B定义为∀x∈X，(A∪B)(x)=max(A(x),B(x))；

5) 模糊集A与B的交A∩B定义为∀x∈X，(A∩B)(x)=min(A(x),B(x))。

定义2[15]设N: F(X)×F(X)→[0,1]是一个映射，称N(A,B)为模糊集A与B的相似度，如果它满足：

(N1) N(X,∅)=0，并且∀A∈F(X)，N(A,A)=1；

(N2) N(A,B)=N(B,A)；

(N3) 当A⊆B⊆C时,N(A,C)≤N(A,B)并且N(A,C)≤N(B,C)。

例1[15]设论域X={x1,x2,…,xn}，A, B∈F(X)，则下面的N1—N15都是模糊集的相似度。

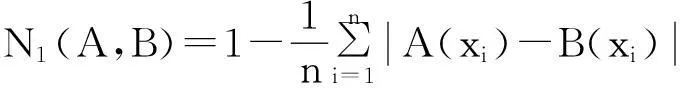
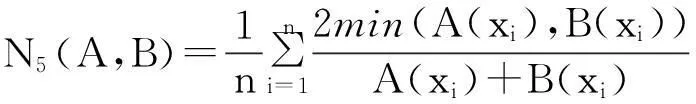
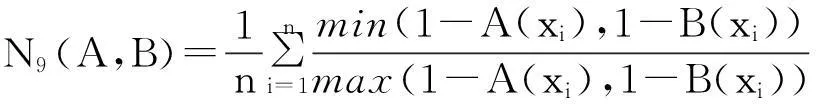
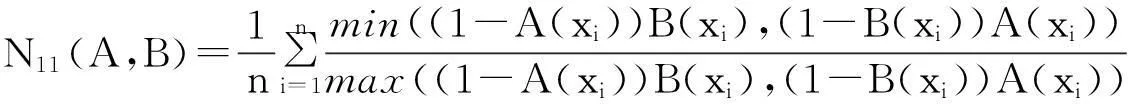
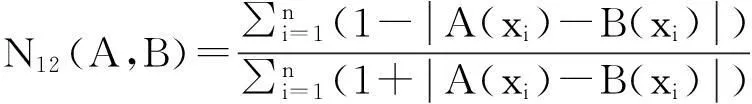
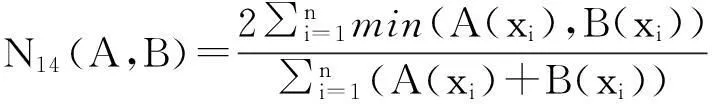
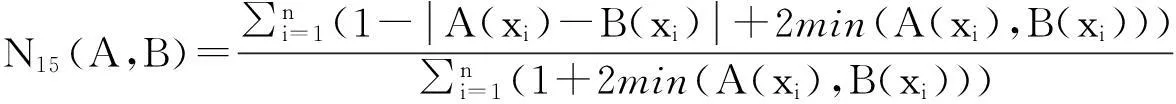
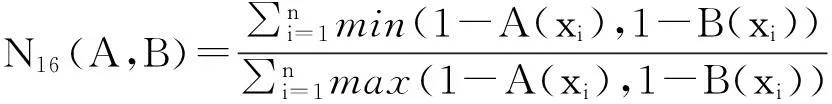
命题1[15]设论域X={x1,x2,…,xn}，A, B∈F(X)，则模糊集的相似度N1—N15满足性质：N(A,B)=1⟺A=B。

1.2直觉模糊集与直觉模糊集的相似度

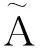
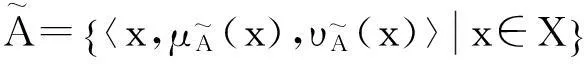
明显地，X上的模糊集A可以用下列方式表示为直觉模糊集：

即直觉模糊集可以看成是模糊集的推广。

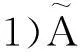
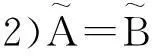
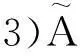
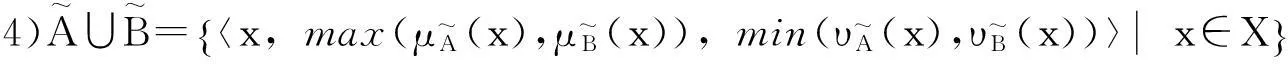
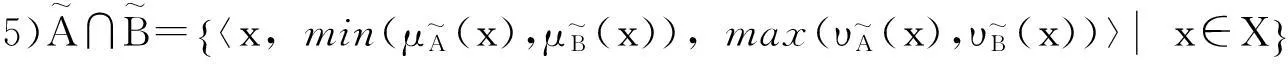
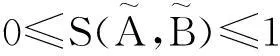
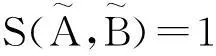
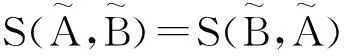
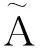
1.3已有的直觉模糊集的相似度

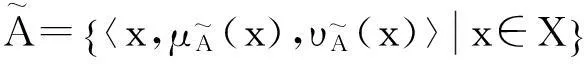
1)Chen[6]提出的相似度

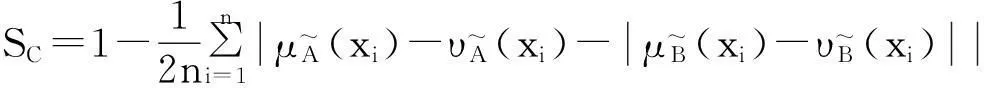
2)Hong等[7]提出的相似度

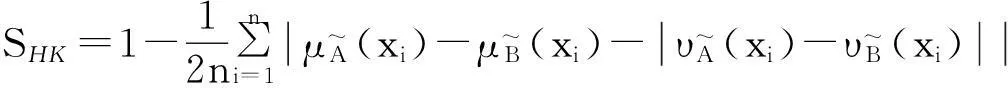
3)Li等[8]提出的相似度

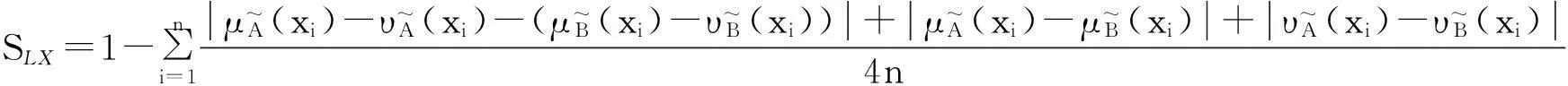
4)Li等[9]提出的相似度

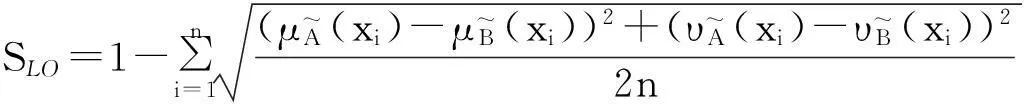
5)Li等[10]提出的相似度

6)Mitchell[11]提出的相似度

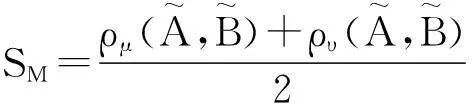
7)Hung等[12]提出的相似度

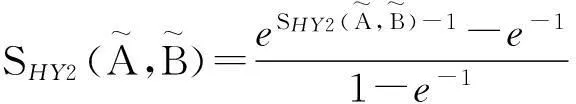
9)Boran等[14]提出的相似度

SBA=1-

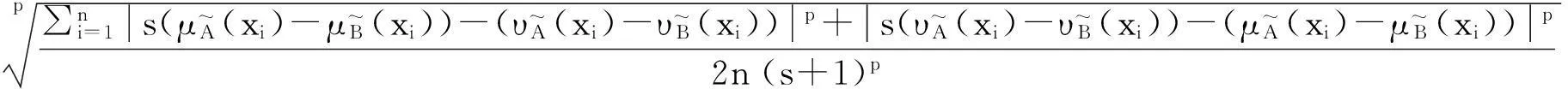
其中，1≤p<∞, 2≤s<∞。

2直觉模糊集相似度的一些新构造方法

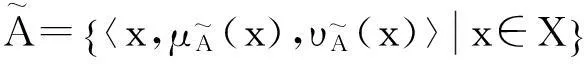
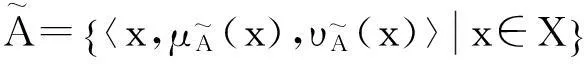
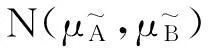
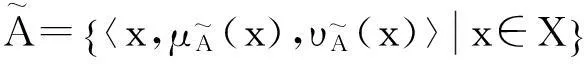
证类似定理1可证。

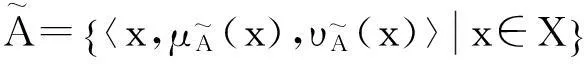
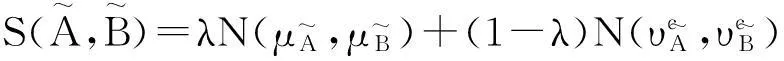
(1)

(1)重视硫磺回收装置过程气中有机硫的控制是很有必要的，在选择尾气处理工艺时，需充分考虑有机硫的贡献值，有机硫含量过高会直接造成硫磺回收装置SO2排放达标困难。

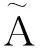
定理3表明，利用模糊集的相似度可以得到直觉模糊集的相似度。这为构造直觉模糊集的相似度提供了一种新的途径。

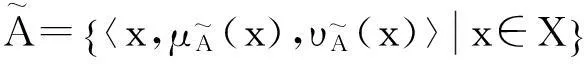
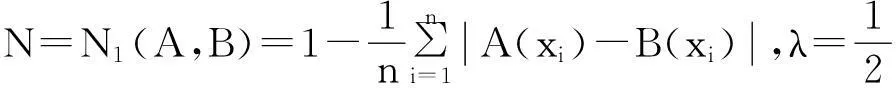
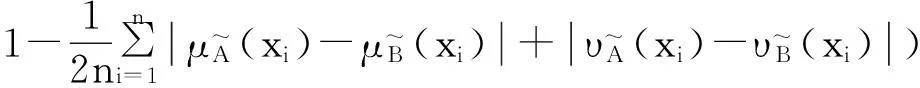
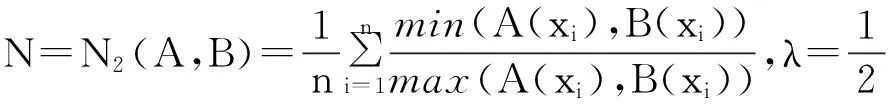
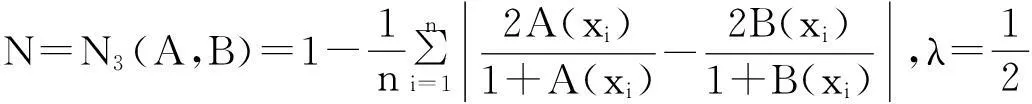
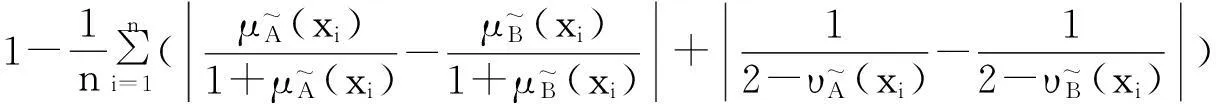
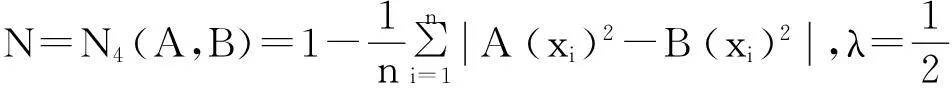
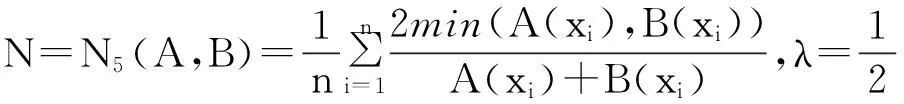
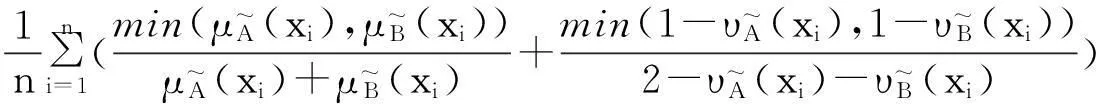
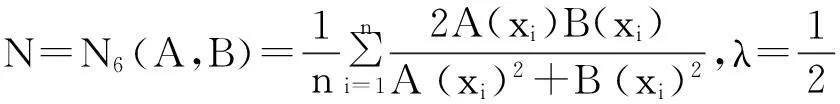
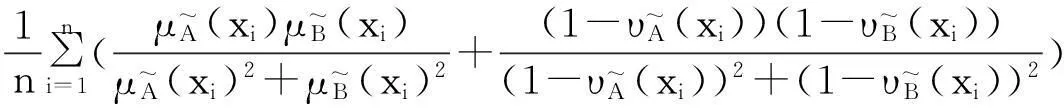
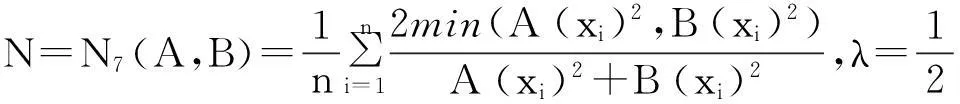
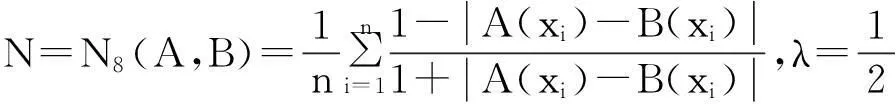
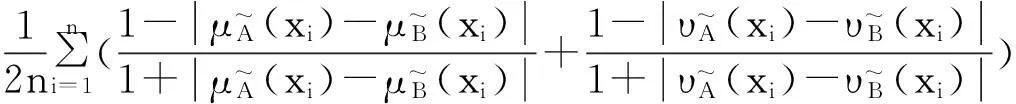
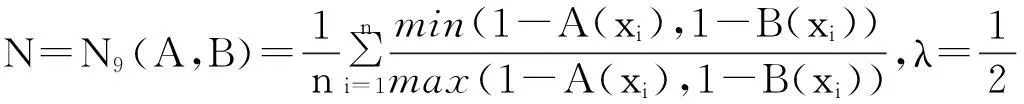
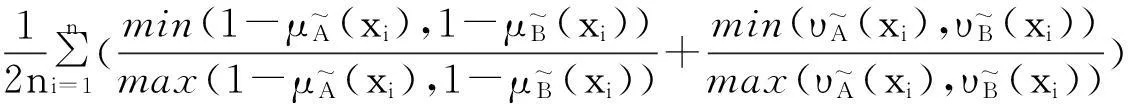
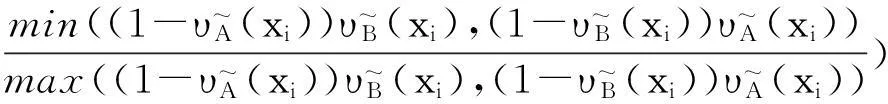
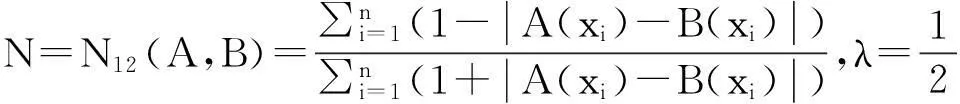
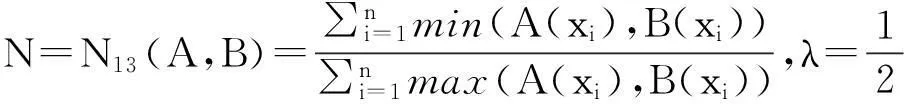
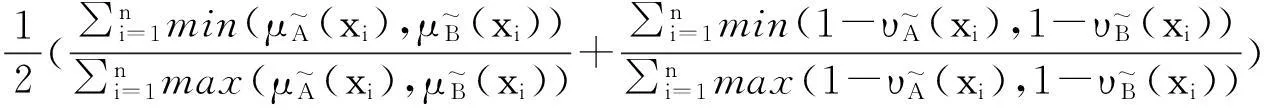
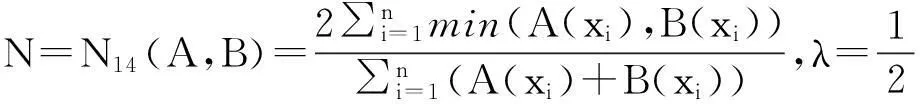
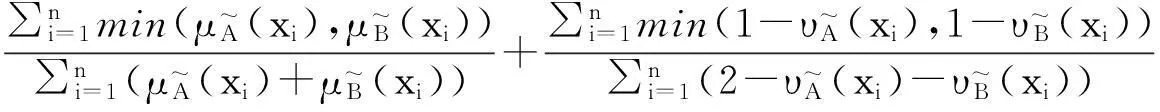
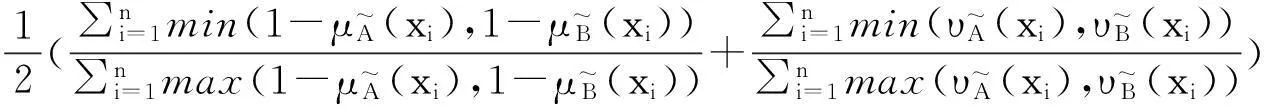
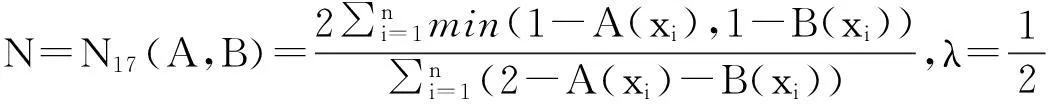
3直觉模糊集相似度在模式识别方面的应用举例

在这一章，给出一个例子来说明直觉模糊集相似度在模式识别方面的应用。

例3[14]设有3个已知模式P1，P2与P3，分别被分标注为C1，C2与C3类。3个模式P1，P2与P3是定义在论域X={x1,x2,x3,x4}上的直觉模糊集，其中：

P1={〈x1,0.5,0.2〉,〈x2,0.5,0.2〉,〈x3,0.4,0.2〉,〈x4,0.5,0.3〉}；

P2={〈x1,0.5,0.3〉,〈x2,0.5,0.2〉,〈x3,0.4,0.2〉,〈x4,0.3,0.5〉}；

P3={〈x1,0.3,0.1〉,〈x2,0.5,0.0〉,〈x3,0.3,0.1〉,〈x4,0.5,0.5〉}。

现在有一个定义在X={x1,x2,x3,x4}上未知模式

Q={〈x1,0.4,0.2〉,〈x2,0.5,0.2〉,〈x3,0.4,0.2〉,〈x4,0.5,0.5〉}。

未知模式Q与3个已知模式P1，P2与P3关于相似度S1—S17的大小计算在表1中。

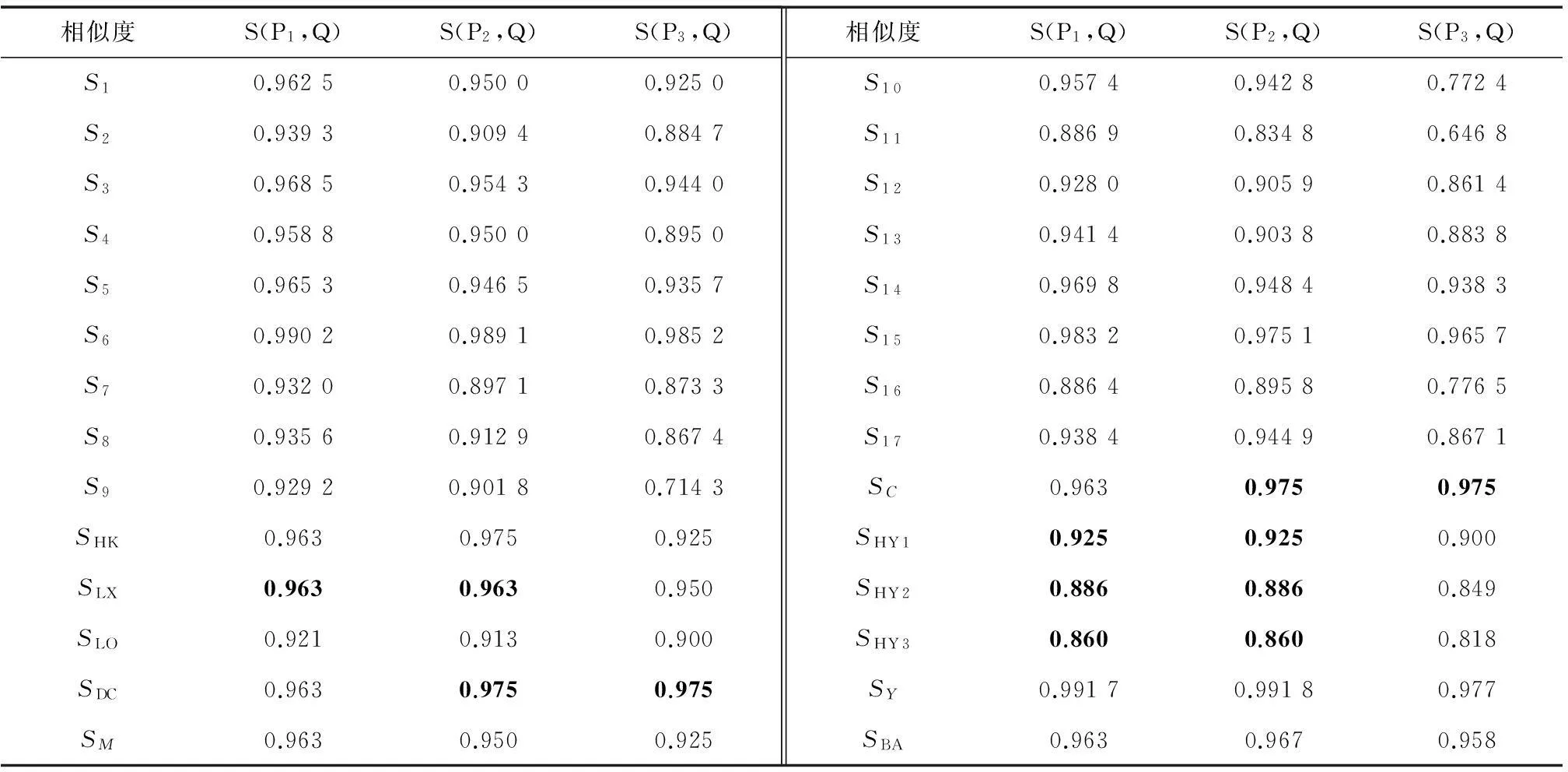
表1　Q与P1，P2，P3的相似度(SDC,SM中p=1，SBA中p=1,s=2)

注：表1中Q与P1，P2，P3关于SC，SHK，SLX，SLO，SDC， SM，SHY1，SHY2，SHY3， SY，SBA的相似度数据来源于文献[14]，其中黑体表示不能识别未知模式Q。

从表1可以看到，未知模式Q在相似度S1—S17下都能进行识别。在相似度S1—S15下模式Q被识别为C1类，与SLO，SM的识别结果一致；在相似度S16, S17下模式Q被识别为C2类，与SHK，SY和SBA的识别结果一致。

4结论

直觉模糊集之间的相似性度量是直觉模糊集理论的一个重要研究内容。本文主要讨论从模糊集相似度的角度研究直觉模糊集相似度的一些构造方法。直觉模糊集的隶属度与非隶属度可以看成是论上的2个

模糊集，因此可以利用模糊集的相似度公式来度量直觉模糊集的隶属度与非隶属度的相似性，从而通过线性组合得到直觉模糊集的相似度计算公式。在以后的研究中，将进一步讨论这些直觉模糊集相似度的性质。

参考文献

[1]Atanassov K. Intuitionistic Fuzzy Sets[J].Fuzzy Sets and Systems, 1986, 20 (1): 87.

[2]Atanassov K. Intuitionistic Fuzzy Sets: Theory and Applications[J].Physica-Verlag HD, 1999, 35(1):1.

[3]Zadeh L. Fuzzy Sets[J].Information and Control, 1965, 8(65):338.

[4]Bustince H, Burillo P. Vague Sets are Intuitionistic Fuzzy Sets[J].Fuzzy Sets and Systems, 1996,79 (3): 403.

[5]Gau W L, Buehrer D J. Vague Sets[J].IEEE Transactions on Systems Man and Cybernetics, 1993,23 (2): 610.

[6]Chen S M. Measures of Similarity between Vague Sets[J].Fuzzy Sets and Systems, 1995,74(2): 217.

[7]Hong D H, Kim C. A Note on Similarity Measures between Vague Sets and between Elements[J].Information Sciences, 1999,115(1): 83.

[8]LI Fan，XU Zhang. Similarity Measures between Vague Sets[J].Journal of Software, 2001 (12): 922.

[9]Li Y, Zhongxian C, Degin Y. Similarity Measures between Vague Sets and Vague Entropy[J].Journal of Computer Science, 2002,29 (12): 129.

[10]Li D，Cheng C. New Similarity Measures of Intuitionistic Fuzzy Sets and Application to Pattern Recognitions[J].Pattern Recognition Letters, 2002 ,23 (1): 221.

[11]Mitchell H B. On the Dengfeng-Chuntian Similarity Measure and its Application to Pattern Recognition[J].Pattern Recognition Letters, 2003,24 (3): 3101.

[12]Hung W L, Yang M S. Similarity Measures of Intuitionistic Fuzzy Sets Based on Hausdorff Distance[J].Pattern Recognition Letters, 2004,25 (14): 1603.

[13]Ye J. Cosine Similarity Measures for Intuitionistic Fuzzy Sets and their Applications[J].Mathematical and Computer Modelling, 2011,53 (s1/2): 91.

[14]Boran F E, Akay D. A Biparametric Similarity Measure on Intuitionistic Fuzzy Sets with Applications to Pattern Recognition[J].Information Sciences, 2014, 255 (1): 45.

[15]Li Y, Qin K, He X. Some New Approaches to Constructing Similarity Measures[J].Fuzzy Sets and Systems, 2014, 234 (1): 46.

(编校：饶莉)

Approaches to Constructing Similarity Measures from Fuzzy Sets to Intuitionistic Fuzzy Sets

LIU Penghui

(SchoolofScience,XihuaUniversity,Chengdu610039China)

Abstract:The similarity measure of intuitionistic fuzzy sets is an important part of the study in intuitionistic fuzzy mathematics. From fuzzy sets view, we proposed construction method of intuitionistic fuzzy set similarity. Firstly, based on fuzzy sets similarity, we obtained measures of similarity between the memberships and non memberships of intuitionistic fuzzy, and then put forward approach to constructing similarity measures from fuzzy sets to intuitionistic fuzzy sets. Secondly, by using of the existing similarity measures of fuzzy sets, we worked out seventeen new similarities of intuitionistic fuzzy sets. Finally, an example demonstrated the application of these new similarities to pattern recognition.

Keywords:fuzzy sets; intuitionistic fuzzy sets; measures of similarity

doi:10.3969/j.issn.1673-159X.2016.02.004

中图分类号：TP18

文献标志码：A

文章编号：1673-159X(2016)02-0017-8

作者简介：刘鹏惠(1973—), 女, 副教授, 主要研究方向为智能信息处理。 E-mail:czclph@163.com

基金项目：国家自然科学基金(61372187); 西华大学网络智能信息处理重点实验室研究基金(SZJJ2012-026, SZJJ2014-052)。

收稿日期：2014-12-31

·计算机软件理论、技术与应用·