一类带吸引项的抛物型方程在记忆边界条件下解的性质

庞凤琴，王玉兰，李慧芳

(西华大学理学院，四川 成都　610039)



·基础学科·

一类带吸引项的抛物型方程在记忆边界条件下解的性质

庞凤琴，王玉兰*，李慧芳

(西华大学理学院，四川 成都610039)

摘要：研究带非线性吸引项的抛物型方程ut=Δu-um在具有时间积分的Neumann边界条件up下解的性质，其中p>0,q>0，m≥1。文章首先证明比较原理成立；其次采用不动点定理建立解的局部存在性；最后通过上下解技巧、积分估计等方法得到方程存在爆破解的充分条件。

关键词：抛物型方程；记忆边界；整体存在；爆破

1引言与准备工作

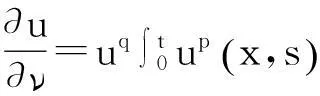
(1)

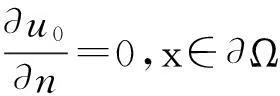
(2)

如前所述，当方程(1)不存在吸引项时，方程的解在p+q≤1时整体存在[11]，本文将证明这个结论对于方程(1)同样也成立。而吸引项的出现会给模型(1)解的爆破结果的研究带来本质的困难，本文将用上下解方法、以p、q、m的关系式给出方程的解发生爆破的充分条件。

上、下解技巧将在本文后面的证明中起到重要作用，为此，先介绍问题(1)上、下解的定义。

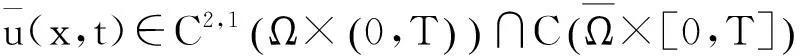
(3)

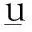
下面证明比较原理。

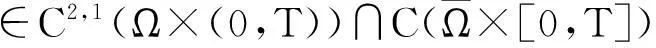
(4)

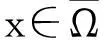
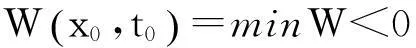
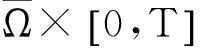
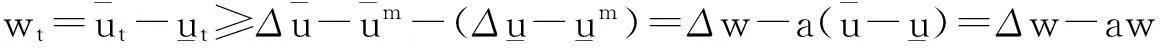
其中：

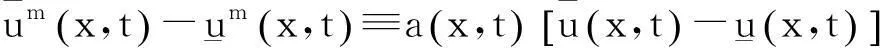
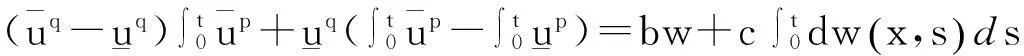
其中:

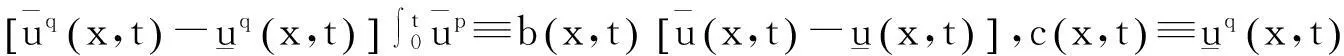
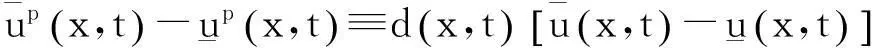
下面我们将利用解的表达式和Banach不动点定理建立问题(1)经典解的局部存在性。用G(x,y,t,τ)表示带有齐次Neumann边界条件的热方程的Green函数。构造算子

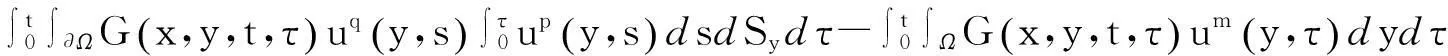
(5)

与文献[15]类似，令

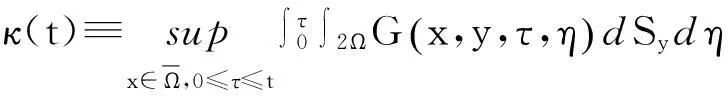
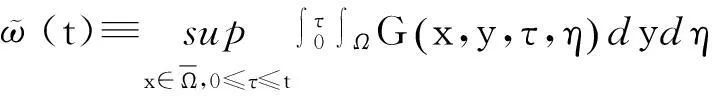
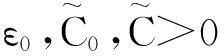
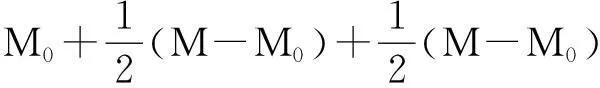
因此，Γ是χ到自身的一个映射，即Γ：χ→χ，其中

对任意的u1,u2∈x，有

‖Γu1-Γu2‖=‖

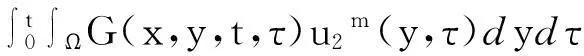
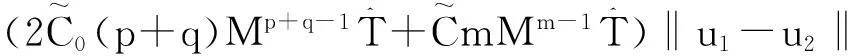
其中ξ1,ξ2,ξ3是介于u1,u2之间的函数。

2有限时刻爆破

定理1当p+q≥m时，问题(1)存在有限时刻爆破的解。

证明为了得到(1)的解在有限时刻爆破的充分条件，考虑如下初边值问题：

(6)

首先证明问题(6)的解u对变量t是单调递增的。令v(x,t)=u(x,t+k)(k>0)，则v满足

(7)

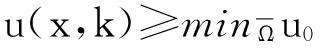
根据u的单调递增性质，我们可以考虑如下问题：

(8)

因为(8)是(6)的一个下解，我们只需证明(8)存在有限时刻爆破的解。

选择h(x)满足如下的方程：

Δh=1，on Ω；

。

(9)

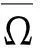
由文献[14 ]知：存在φ(ζ)满足

(10)

通过计算，可以得到

(11)

对(11)第2个等式两端同时乘以φ'(ζ)并在(1,ζ)上积分得到

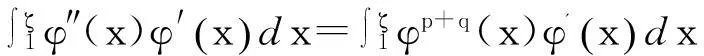
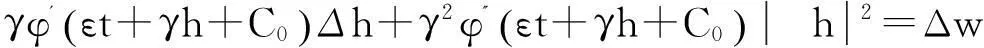
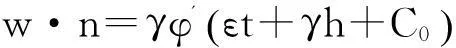
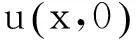
3整体存在

定理2当p+q≤1时，(1)的每一个非负解都整体存在。

证明由文献[11 ]可知，当p+q≤1时热传导方程

(12)

的每一个解都整体存在。显然，问题的解为(1)的上解，因而由比较原理可知问题(1)的解整体存在。

4结论

由定理1、定理2可知：当p+q≥m且u0充分大时，问题(1)的解都在有限时刻爆破；而当p+q≤1时,(1)的所有解都整体存在。

参考文献

[1]Chadam J M, Yin H M. An Iteration Procedure for a Class of Integrodifferential Equations of Parabolic Type[J]. Integral Equations Appl,1989，2(1): 31.

[2]Souplet P. Blow-up in Nonlocal Reaction-diffusion Equations [J].SIAM Math Anal,1998, 29(6): 1301.

[3]Li F C, Huang S X, Xie C H. Global Existence and Blow-up of Solution to a Nonlocal Reaction-diffusion System[J].Discrete Continu Dynam Systems,2003，9(6): 1519.

[4]刘其林，邓卫兵，谢春红.一类退化抛物方程解的存在性及爆破速率[J].数学学报，2003，46(4): 775.

[5]吕峰，樊明书，徐思.一类具有非线性记忆的半线性抛物方程解的爆破速率[J].四川大学学报(自然科学版)，2009，46(1): 29.

[6]Li Y X, Xie C H. Blow-up for Semilinear Parabolic Equations with Nonlinear Memory[J]. Z Angew Math Phys,2004, 55(1): 15.

[7]石立新，程正琼.一类具有非线性记忆和吸收项的半线性抛物方程解的爆破[J].四川大学学报(自然科学版)，2008, 45(6): 1313.

[8]Liu D M, Mu C L, Ahmed I. Blow-up for a Semilinear Parabolic Equation with Nonlinear Memory and Nonlocal Nonlinear Boundary[J].Taiwanese Journal of Mathematics, 2013,17(4):1353.

[9]王明新.非线性抛物型方程[M].北京:科学出版社,1997.

[10]王玉兰，陈利娅，李慧芳.具有局部化反应项的p-Laplace方程的整体存在指数[J].西华大学学报(自然科学版)，2014，33(4)：38.

[11]Anderson J R, Deng K，Dong Z.Global Solvability for the Heat Equation with Boundary Flux Governed by Nonlinear Memory[J].Quart Appl Math,2011，69(4): 759.

[12]Deng K, Dong Z. Blow up for the Heat Equation with a General Memory Boundary Condition[J].Communications on Pure Appl Anal,2012，11(5): 2147.

[13]陈继芹，王玉兰，宋小军.一类带记忆边界条件的抛物型方程的爆破问题[J].四川大学学报(自然科学版)，2014，51(2)：229.

[14]Anderson J R, Deng K. Global Solvability for the Porous Medium Equation with Boundary Flux Governed by Nonlinear Memory[J].Math Anal Appl,2015, 432(2)：1183.

[15]Deng K, Kwong M K, Levine H A. The Influence of Nonlocal Nonlinearities on the Long Time Behavior of Solutions of Burgers’ equation[J]. Quart Appl Math, 1992，50(1): 173.

[16]Hu B, Yin H M. Critical Exponents for a System of Heat Equations Coupled in a Non-linear Boundary Condition[J].Math Methods Appl Sci,1996，19 (14): 1099.

(编校：叶超)

The Properties of a Parabolic Equation with Absorb Term and Memory Boundary Condition

PANG Fengqin,WANG Yulan*,LI Huifang

(SchoolofScience,XihuaUniversity,Chengdu610039China)

Abstract:In this paper, we studied the following parabolic equation with absorb term ，x∈Ω,t>0under the Neumann boundary up,where p>0,q>0，m≥1. We proved a comparison principle, and then established the local existence of solutions via a fixed point argument. Finally we obtained the sufficient condition for the existence of blowup solutions by using the super-sub solution technique and integral methods.

Keywords:parabolic equation； memory boundary; global existence; blowup

doi:10.3969/j.issn.1673-159X.2016.02.016

中图分类号：O175.2

文献标志码：A

文章编号：1673-159X(2016)02-0082-6

*通信作者：王玉兰(1979—)，女，副教授，博士，主要研究方向偏微分方程。E-mail：wangyulan-math@163.com.

基金项目：四川省教育厅重点科研项目(14ZA0119)；西华大学研究生创新基金(ycjj2014034)。

收稿日期：2015-05-05