流激噪声数值计算方法及声学积分面影响性研究

张 楠，王 星，谢 华，李 亚

（中国船舶科学研究中心 a.水动力学重点实验室；b.船舶振动噪声重点实验室，江苏 无锡 214082）

流激噪声数值计算方法及声学积分面影响性研究

张 楠，王 星，谢 华，李 亚

（中国船舶科学研究中心 a.水动力学重点实验室；b.船舶振动噪声重点实验室，江苏 无锡 214082）

在流声耦合领域中，水下航行体复杂流动与流激噪声研究具有重要的学术意义与实用价值。文章对FWH声学类比方法、渗流FW-H声学类比方法、Kirchhoff方法与Powell涡声理论进行了物理内涵与数学公式的详细比较；然后利用大涡模拟结合四种声计算方法数值计算了三维NACA0015机翼、机翼/圆柱结合体、方腔产生的流激辐射噪声，并与国内外试验结果进行了对比，分析了四种声计算方法的计算精度与计算效率；最后，对围壳流激噪声进行了数值预报与试验验证，计算了围壳在不同水速下的流激噪声变化规律，并探讨了声学积分面对计算结果的影响。

流激噪声；大涡模拟；FW-H声学类比；渗流FW-H声学类比；Kirchhoff方程；Powell涡声理论

0 引 言

流/声耦合（fluid-acoustic coupling）是一个新兴的研究领域，涉及流体力学和声学两个经典学科，其科学内涵的前瞻性与新颖性广受瞩目，主要研究非定常流动机理及其远场声辐射特征和规律、复杂流动与流激噪声数值预报与试验测量、流动与噪声的控制等科学问题。该领域的研究具备应用基础研究的明显特征，需要深入的理论分析、繁难的数值计算和精细的试验验证，其技术难度是不言而喻的。随着科研领域对于学科交叉研究的高度重视与持续发展，流/声耦合研究已成为水动力学领域的研究热点，具有广阔的发展前景。

流/声耦合研究主要包括两类：（一）在研究流动诱导远场辐射噪声的过程中，仅关注流动产生的噪声，不考虑噪声对流动的反作用，在目前国内外公开发表的相关论文中主要讨论的是这类情况。一般而言，噪声不会影响流动的假设在大多数情况下都是成立的。比如，在喷气噪声问题中，一般只有万分之一的湍流能量会转变为声能，即便在火箭热喷射问题中，声转化效率很高的情况下，也仅有不到百分之一的湍流能量会转变为声能，在水动力学问题中这个比例就更小了。因此在一般工程问题中，特别在马赫数较低的情况下，仅关注流动产生的噪声，而不考虑噪声对流动的反作用，是合理可行的；（二）关注流/声相互作用（flow noise interaction），亦即探讨流动产生噪声而噪声反过来又影响流动发展变化的问题，这种情况在工业界中极少出现，一般仅存在于核反应堆与火箭发动机的燃烧室中。本文只涉及第一类研究，不讨论第二类问题。

当飞机、舰船、潜艇等运载器在流体介质中运动时，物面边界层由层流发展为湍流。层流为一层层不掺合的平滑稳定流动，湍流是各层剧烈掺合且在时间和空间上都不断变化的流动状态。在运载器机动工况下，还会有流动分离发生，会出现明显的涡旋结构。这些非定常流动一方面直接产生辐射噪声，国外一般称为流激噪声或流致噪声（flow induced noise或flow generated sound）[1-5]；另外一方面，非定常流动中的瞬态速度扰动产生脉动压力，脉动压力激励物面弹性结构振动并产生二次辐射噪声，国外一般称为流激振动噪声（flow induced vibration and noise）[1-5]。在以往，国内水动力学界的学者也常用流噪声、流动噪声、流体动力噪声指代第一类噪声，目前基本用水动力噪声这一术语来涵盖这两部分噪声[6-10]。

按照流体辐射声时外部空间的形式可将流激噪声问题分为下列三种问题[2，11]：

（1）自由空间问题：声源区没有物面存在，外部边界远离声源，而且在空间内没有明显的障碍物影响声辐射，近似认为声源向无限大区域辐射声。例如常见的自由湍流发声、喷射流动发声问题等。

（2）有物面存在的自由空间问题：物面区域作为声源区，而外部边界远离声源，声向外部空间辐射时没有明显的障碍，表现为流体流经静止的物面发声，或者物体在流体介质中运动发声，例如飞机和舰船航行时的流体动力噪声问题，螺旋桨旋转时的流体动力噪声问题等。

（3）有限空间问题：导管、管道或管路中的流动发声问题。

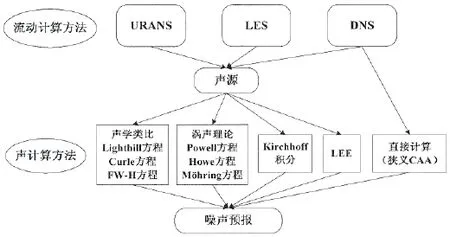
图1 流激噪声数值计算方法Fig.1 Numerical simulation approach for flow induced noise

流激噪声数值计算方法主要有直接计算方法和积分方法两类。在早期，人们习惯于把直接计算方法称为计算气动声学（Computational AeroAcoustics-CAA），目前，国际上对CAA的定义更为宽泛，基本可以涵盖这两类方法，Wagner等人（2007）[12]在其文献中给出了详细说明。积分方法中最著名的就是声学类比方法，另外还有Kirchhoff积分法与Powell涡声理论等其他方法。流激噪声数值计算方法的一般分类与计算流程见图1。

在直接计算方法中，声波的产生与传播都通过直接求解非定常可压缩的NS方程得到，即直接从计算中提取所有的声信息，用到CFD中的直接数值模拟（DNS）方法。计算时，接收器必须布置在计算域内，直接监视接收器处的声压脉动，要求无反射的边界条件（NRBC），避免发生人工反射声对主声场的干扰。与一般的CFD计算（如RANS、LES、DES等）相比，DNS对计算方法的要求更高，需要更多的网格数、更高的空间和时间精度，而且要求在从声源到接收器的全域内有足够的空间分辨率，否则求出的声波很快就耗散掉了。对于远场噪声计算，还面临计算量过大的困难，有些算例即便在目前的并行计算机上也难以实现，所以一般只用于计算近场噪声。由于直接计算需要高阶离散格式以使得声波传播到远场，所以数值离散造成的误差常会成为伪声源项，从而对正确的计算结果造成一定程度的干扰。

与直接计算相比，在计算远场噪声时，Lighthill（1952）[13]创立的声学类比方法更为可行，更有实用价值。在声学类比方法里，流动特征通过求解合适的非定常流动方程得到，控制方程可以是可压缩的流动方程，也可以是不可压缩的流动方程，然后通过格林积分公式来预报远场噪声，从而将微小的声学脉动从较大的流体力学脉动中分离出来。声学类比方法的技术思路就是使用非定常的CFD技术求解流场，作为等效声源项输入到声场计算中，然后利用波动方程的解，将声源项产生的脉动进一步辐射到外场。计算流场时，可以采用非定常的RANS方法（URANS）、离散涡模拟（DES）以及大涡模拟（LES）等方法。大涡模拟由于能够较好地模拟湍流脉动量，所以是一种比较精确的方法。从本质上说，声学类比方法就是将声波的产生与传播进行解耦，使得人们在分析中可以先将流动解单独分离出来，从而作为声学分析的一种输入，在低马赫数下，声场对于流场的影响完全可以忽略，所以上述解耦也是可行的。声学类比方法只需对声源区域的流场进行CFD计算，对计算量和差分格式的要求都较直接计算方法为低。在声传播的过程中不存在频散与耗散。可以选择多个声源面、多个接收器，而且接收器也可以布置在计算域外。这种方法的局限就在于一般只能预报声波向自由空间的传播，不能考虑声源区之外的物体对声波的反射与散射，也不处理折射与透射，也不能考虑声对流体的影响。一般在低马赫数下声能比流体能低几个数量级，声对流体的影响也基本不用考虑。

从理论上讲，只要知道流体运动的物理特性，无论是运动源还是力源，从Lighthill方程出发都能求解其声辐射，流体运动与声辐射看似独立的两个物理现象从此联系起来，流体动力声学作为一门学科从此发展起来，运动体引起的流动噪声问题也逐渐进入学者的视野。1955年，Curle采用Kirchhoff方法将Lighthill理论进行推广，导出了著名的Curle方程，该方程可以处理静止固体边界的影响[14]。从Curle方程可知，一个四极子源与固体边界的相互作用会产生新的低阶的偶极子源，辐射效率增强，这正反映了声学的复杂性。随后在1969年，Ffowcs Williams和Hawkings应用极为有效的数学工具—广义函数法将Curle方程进行拓展，使之可以处理固体边界在流体中运动的发声问题，得到了经典的FW-H方程[15]。1974年，Goldstein用格林函数方法推导出了广义的Lighthill方程[16]。从这个方程我们可以清晰地知道Curle方程和FW-H方程均是该方程的特定表达。上述基于Lighthill思想的各种方法统称为声学类比方法。在近代逻辑学中，类比法是根据两个（或两类）不同对象的部分属性相似，从而推出这两个（或两类）对象的其他属性也可能相似的一种推理方法。类比法是归纳法和演绎法的中间状态，它径直从一个特殊领域走向另一个特殊领域。可以这样说，类比是通常认识过程的缩合形式，既包含归纳的成分又包含演绎的成分。类比的推理方向是从特殊到特殊，即从一个对象的特殊知识过渡到另一对象的特殊知识。

声学类比方法属于积分方法，此外，在这类方法中还有Kirchhoff积分法、线性欧拉方程法以及Powell创立的涡声方程方法，它们都有各自适用的范畴。Kirchhoff积分法要把流动区域分为线性区域与非线性区域，控制面要布置在线性区域中，解对控制面的位置很敏感，而且需要将压力的法向导数作为声学计算的输入变量，这些都给计算带来了困难。线性欧拉方程（LEE）方法是一种较新的方法，其适用于求解非均匀流动中声波的传播，一般用来求解存在非均匀流动的低扰动区域内的声波，常在较高马赫数下使用，考虑到数值耗散与频散的影响，一般仅用来求解中场（mid-field）噪声。

在Lighthill方程提出之后，Powell（1964）[17]将涡量描述引入该方程，进一步研究了涡运动和声产生之间的联系，推导出了Powell方程（涡声方程），开创了涡声理论，这一理论实质上是Lighthill理论在低马赫数下的一个演化。Powell方程指出：涡是低马赫数下等熵绝热流动发声的根源。由于涡量分布往往集中在狭小的流动区域，所以它是紧致的偶极子源。研究者普遍认为，Lighthill理论在预报流动噪声方面有着无可比拟的实用价值，而在探索流动发声的内部机制方面，Powell理论则以其简洁深邃的内涵显示出了极大的优势。对于涡声理论的进一步发展是Howe（1975）[18]的工作，他引入驻焓（stagnation enthalpy）的概念，考虑了熵变化和平均流对流动发声的影响，导出描述声音在气流中传播的非齐次方程—Howe方程。Howe方程是描述由于涡量和熵的变化以及其相互作用而发声的声学普遍公式，它也描述了与声音相关联的非线性现象的相互作用。Howe方程指出如不存在涡旋和熵梯度，则气流不会发声，声源只集中在那些存在有涡量及熵梯度的区域。Howe方程只有当无旋和等熵时才是封闭的，多数情况下，此方程不封闭，只有再引进另外的旋度及熵的扰动量方程才能求解。Howe（2003）[19]进一步指出：气体的非定常粘流运动是声音、涡旋和熵运动成分的叠加和相互作用组成的，非线性效应导致上述运动的相互转变，这些问题是摆在连续介质力学和气动声学面前的艰巨任务，当然，这些内容也远远超出一般流动声学的研究范畴。

在本世纪之前，由于计算条件的不足，对声源项难于准确求解，许多流激噪声计算预报方法都停留在形式解的阶段，仅能用来进行理论分析。近年来，随着计算机硬件性能的大幅提升以及并行技术的飞速发展，国内外对于流激噪声的计算研究都广泛开展起来。在国内，中国船舶科学研究中心（CSSRC）在潜艇水动力/流场/噪声计算方面已经开展了大量工作，从水动力到脉动压力进而到流激噪声，通过不断积累和完善，取得了一些进展[20-29]。这些工作为今后的研究提供了技术支撑，所积累的计算经验可资今后研究借鉴。上述研究结果往往是用某一种流激噪声计算预报方法进行研究，对于各种预报方法的异同和它们之间的联系尚没有做深入比较和分析，国外有一些研究[30]，但国内的研究还很少。

本文在以往研究的基础上，对于原初与渗流FW-H声学类比方法、Kirchhoff方法、Powell涡声理论进行了理论分析和公式推导，从物理概念和数学内涵上对它们进行了比较分析，然后结合大涡模拟方法完成了建模与计算分析，验证了数值计算方法的计算准确度和工程实用性，并探讨了声学积分面的影响。本文中的流场计算基于商用软件FLUENT二次开发完成，四种流激噪声计算方法利用自编程序实现。

1 流动计算方法

1.1 大涡模拟方程

经过网格滤波的连续性方程和NS方程可以表示为：

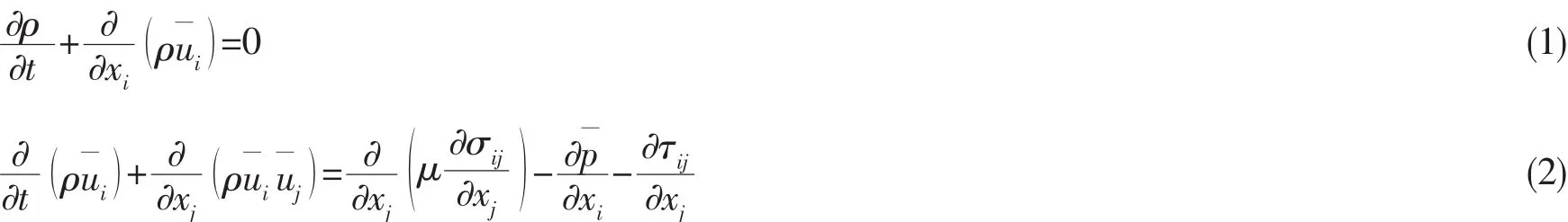
其中：σij为分子粘性引起的应力张量；τij为亚格子应力，需用亚格子模型进行模拟。

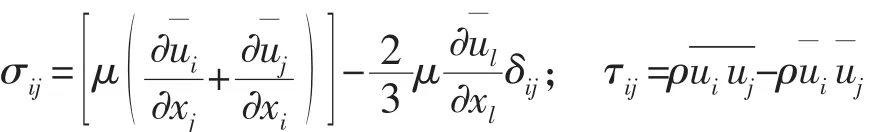
其中：第一项称作Leonard项，也称作外散射项（outscatter term），代表两个大涡间的相互作用，以产生小尺度湍流；第二项称作交叉项（cross term），代表大、小涡间的相互作用，其间能量可以从大涡向小涡传递，也可以反向传递，从小涡传向大涡，但总体平均起来，能量还是以从大涡向小涡传递为主；第三项称作反散射项或逆散射项（backscatter term），代表小涡间的相互作用以产生大涡，并带来能量从小涡到大涡的传递。过去曾认为，既然各项的物理意义不同，应该分别用不同模型去近似它们，但是由于模化技术尚未完善，分别模化未必准确，所以意义不大，还是倾向于合在一起作总体上的模化。本文采用动态Smagorinsky模型对亚格子应力进行模拟，引入布西内斯克（Boussinesq）假设，如下式所示：

其中：τkk为亚格子应力中的各向同性部分，不用进行模拟；为滤波尺度下的应变率张量；C为动态系数；△为网格滤波尺度；。Smagorinsky详细的动态 模型描述请参见文献[31-32]。

2 噪声计算方法

2.1 FW-H与渗流FW-H声学类比方法

FW-H方程的计算优势较明显。首先，FW-H方程右端的三个源项有明确的物理意义，交互干扰效应较小，有利于研究者了解噪声产生的根源及传播特征。单极子声源由物体几何形式与运动特征决定；偶极子声源由流体作用在物体上的非定常力决定；四极子声源由流体运动时产生的Lighthill应力张量决定，其中包含了各种非线性效应，如流场中的涡、湍流、激波、非线性波传播与波陡、当地声速的变化等等因素的影响。其次，将三个源项相互分离，也使得数值计算能够方便进行，而且当某种声源不起主要作用时，可将其忽略，从而减小了计算量。针对不同的声源，可以开展不同的降噪方法研究，使得控制目的更加明确，从而有利于提出实用效果明显的安静化措施。最后，基于FW-H方法的计算软件与计算程序相对来说比较成熟，已经在工业气动声学问题中得到广泛应用和验证，可靠性与鲁棒性得到了检验。

传统FW-H方法的主要缺点在于计算四极子声源的发声需要整个源域内的体积分，不但计算量是非常大的，而且比较复杂，难于精确完成，一般都要做些简化处理，因此，许多研究者在研究低马赫数下流动发声时，普遍认为四极子声源的影响较小，往往将其忽略，从而减小计算工作量，而实际上，四极子源的影响在某些频段下还是比较明显的，简单地将其移除也并不是很合适。在上世纪九十年代，研究者利用Kirchhoff方法的思想将传统FW-H方法进行拓展[30，36]，创立了渗流FW-H方法，就是将源项在一个虚拟的渗流控制面（porous or permeable surface）上进行积分，这既保证了四极子源的贡献，又减小了计算工作量。而且渗流FW-H方法对于积分面位置的选择不敏感，放置在近场与远场都可以。但是渗流面的几何形式要结合大量具体计算的实践经验进行选择，有时也是颇伤脑筋的一桩事情。

FW-H声学类比方程如下：

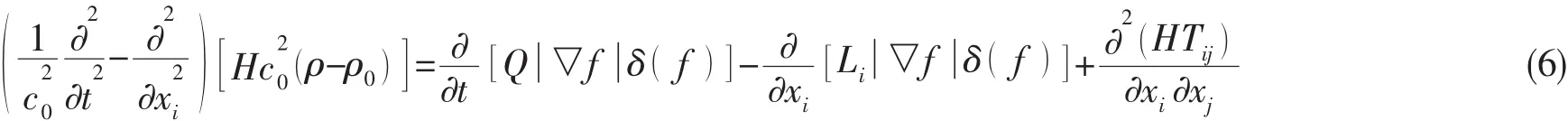
FW-H声学类比方程的远场解如下：

单极子噪声：

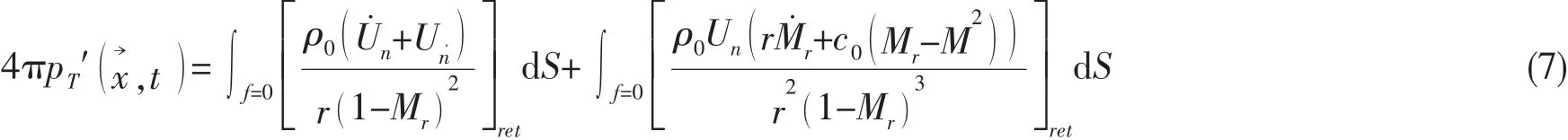
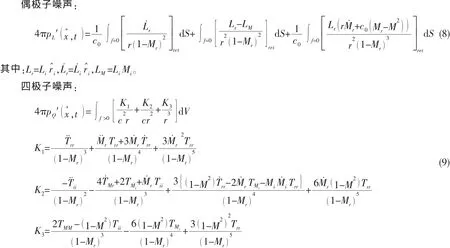
原初的FW-H方程远场积分解包括两个面积分（7）式与（8）式，以及一个体积分（9）式。由于求解流激噪声的网格数量很多，所以求解体积分的工作量就变得非常巨大，给工程实用带来很大麻烦，因此国外研究者借鉴了Kirchhoff积分思想（源于电磁场求解的Kirchhoff-Helmholtz定理），创立了渗流FW-H声学类比方法，此方法与原来的FW-H声学类比方法的控制方程完全相同，仅在远场解的表达上有差异。所谓"渗流"，即在计算域内做一包含主要流体动力声源在内的控制面，此控制面是虚拟的，只在积分时使用，而流动可以自由穿过，不受任何影响，因此命名为渗流面。如果控制面布置在物体表面上，而且假设物体是不可穿透的，那就可使用原初意义上的经典FW-H方法。若控制面逐渐远离物面，亦即此控制面相对物面有一定距离，声源完全被包围在此控制面中，就可使用渗流FW-H方法，此时只需在此控制面上做两个面积分，就可以完全得到三种声源的贡献，不用去做体积分，因而计算效率大大提高。在实际计算时，可以根据可行性并且兼顾计算效率，灵活方便地布置控制面，这正是此种方法的优点。渗流FW-H方法具有很高的灵活性和实用性。

2.2 Kirchhoff方程

Kirchhoff方程的解仅需要面积分，不需要体积分，计算量较小，这是它的主要优势，因而在过去也得到一些应用。但与FW-H方程不同的是，Kirchhoff方程中的源项完全是一种数学表达，很难建立起清晰的物理意义，因此，工程领域的研究人员不太愿意使用这种方法。由于它缺乏清楚的物理概念，所以在工程设计中也不太可能提供很有价值的指导原则。求解Kirchhoff方程时，积分面必须布置在线性流动区域（linear flow region），即流动物理量线性变化的区域，这种区域的准确几何形式是很难严格界定的，实际处理时一般只能将积分面布置在远离物体的远场，实践证明，Kirchhoff声计算方法对于积分面位置选取十分敏感[30]，而且此方法还需计算压力沿积分面法向的导数，这无疑也增大了计算难度。同时，将同样的处理FW-H方程远场解的数值方法施用于Kirchhoff方程时也会遇到一些新的困难，因为Kirchhoff积分面往往布置在远场，面积较大，导致延迟时间差异明显，给数值计算带来麻烦。

推导Kirchhoff方程时所用到的数学技巧与推导FW-H方程是相似的。表面f=0内部包含所有的声源。声压定义如下，其他变量照此处理：

下面讨论Kirchhoff方程与FW-H方程之间的联系。为此，我们将FW-H方程进行加减项处理，即在FW-H方程右面先加上QKIR，再减去QKIR，为了数学表达简便起见，将FW-H方程源项中的剪应力τij省略（τij的物理影响也确实很小），并不影响最终结论，因而得到：

利用连续性方程与动量方程，以及下式：

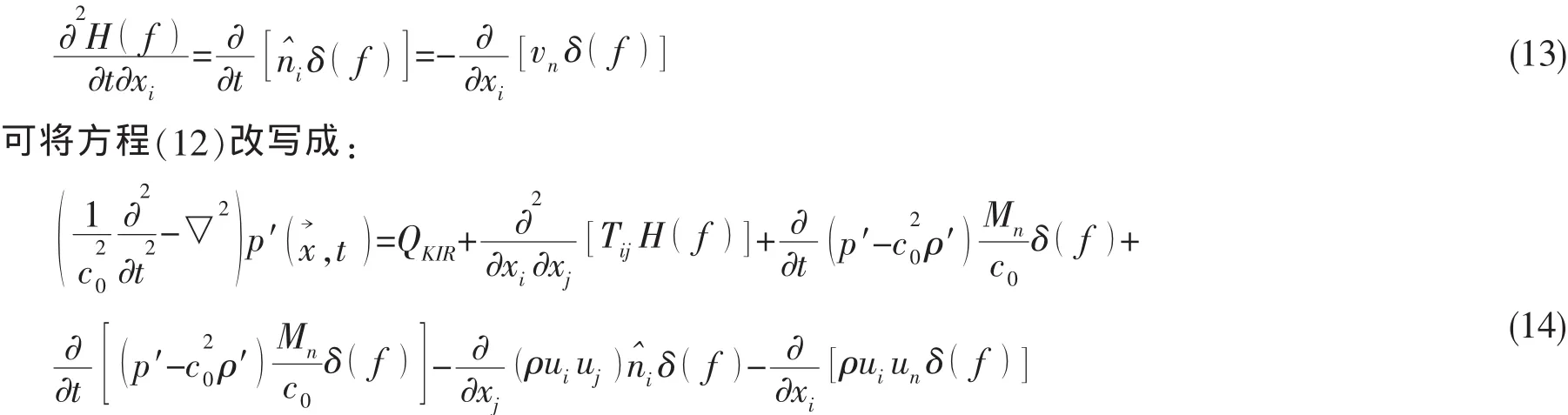
也就是说，FW-H方程变成了Kirchhoff方程，这说明只要积分面处于流动的线性区域，则FW-H方程与Kirchhoff方程是等价的[30]。

Kirchhoff方程的解为：

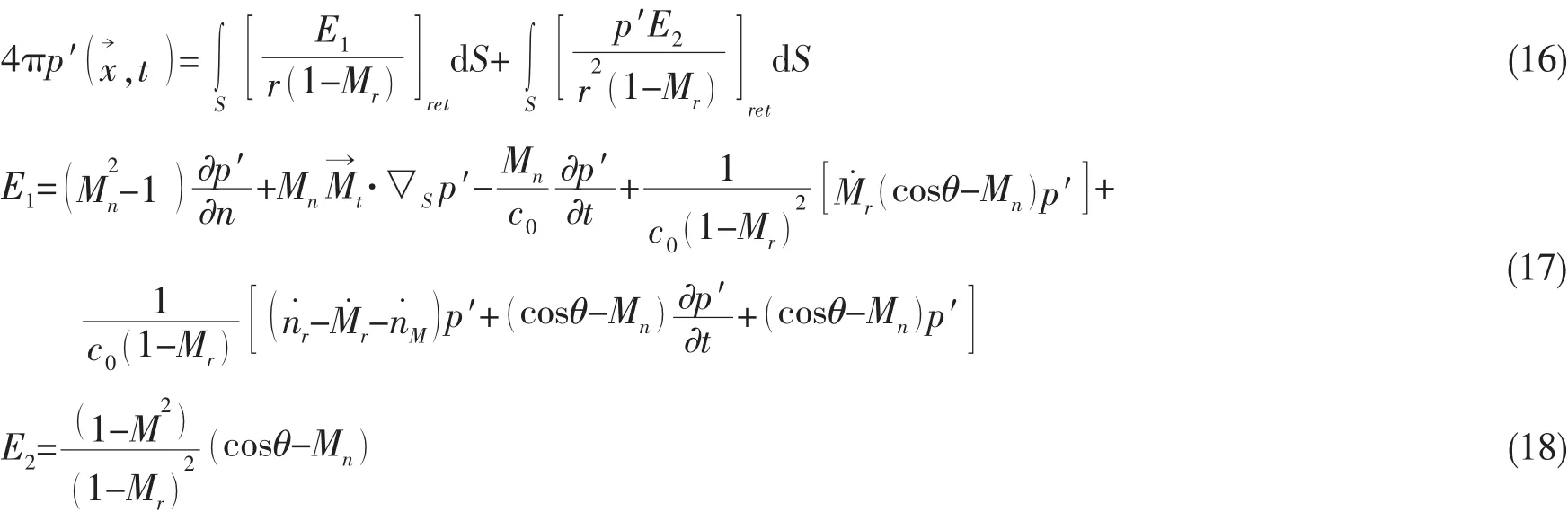
其中：M为控制面的马赫数矢量；r为声源与观测者之间的距离；θ为源发射角；为控制面的单位法向

i矢量为与控制面相切的马赫数矢量；▽S为控制面梯度矢量；，变量上的小圆点表示源时间导数，此时控制面位置保持不变。

2.3 Powell涡声理论

作者对于Powell涡声方程的详细分析请参见文献[28]，在本文中简要描述。在研究湍流诱发噪声问题中，关键的一步就是构建流动声源数学公式，也就是如何在数学表达上将流体运动转换为声源。Lighthill建立的声学类比方法是将雷诺应力、压力、剪应力进行组合作为声源，通过面积分和体积分得到远场辐射噪声，在工程实际中发挥了巨大作用，但是，声学类比理论尚不足以深入了解流动发声的机理和细节，因为众所周知，涡会产生噪声，但是在声学类比理论中没有辨识出涡动力学特征，而且Lighthill应力张量在空间分布比较疏散，不利于计算，而涡量的分布相对集中，便于计算。Powell深入研究了流体动力与噪声之间的关系，并将它们与涡运动联系起来，就得到了涡运动产生噪声的机理与数学表达式。

本文求解的Powell涡声方程如下：

通过对Lighthill方程进行变换，也可以推导出Powell涡声方程，说明在低马赫数下二者等价，推导细节请见文献[28]。

Powell方程的远场解可用密度摄动表达如下：

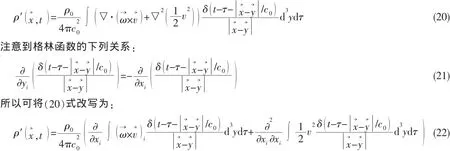
3 数值求解

流动控制方程的时间项采用二阶隐式格式离散，动量方程采用限界中心差分格式离散，压力速度耦合采用SIMPLE算法。利用代数多重网格方法加速收敛。计算中时间步长△t=1×10-5s。采用FFT结合Hanning窗处理非定常信号时间序列。本文中的前三个算例在无锡超算中心并行求解完成，第四个算例在中国船舶科学研究中心自建并行计算机集群上求解完成。

4 计算结果分析

4.1 FW-H声学类比方程（原初解与渗流解）与Kirchhoff方程的计算结果比较

流激噪声测试数据在航空领域是很多见的，但大都是高马赫数下的流动发声，选择这些试验数据来验证本文所建立的主要适用于水动力学领域的计算方法并不合适。作者经过文献检索，选择Devenport（2010）在美国弗吉尼亚理工大学（Virginia Tech）消音风洞（Anechoic Wind Tunnel）中所做的机翼流噪声试验数据来验证本文所建立的计算方法，模型尺度与风速大小都较合适。试验设备、试验仪器、试验方法等细节详见参考文献[33]。计算模型与试验模型保持一致，都为三维NACA0015翼型，弦长C=0.61 m，展长L=1.8 m。试验风速V=30 m/s，基于弦长的雷诺数为Re=1.3×106。全域采用结构化网格计算，网格数为675万。壁面y+≈1～5。空气中参考声压pref_air=20 μPa。计算域与计算网格划分见图2。边界条件如下：速度入口：翼型首部向前10倍弦长，设置风速；压力出口：翼型尾部向后20倍弦长，设置流体静压；壁面：翼型表面，设置无滑移条件；滑移壁面：计算域侧面，设置零剪应力条件。本节计算了翼型在攻角为0°和8°下的流场、脉动压力与流激噪声，并与试验结果进行了对比分析。图3给出了中展面（mid-span plane）上压力与流线分布，从图中可以看到有攻角情况下压力分布与无攻角时相比明显不同，8°攻角下翼型尾部有明显的流动分离，产生清晰的涡旋结构。

为了进一步说明大涡模拟定量预报流动非定常特性的能力，本文又计算了两个攻角下机翼表面脉动压力频谱，并与试验结果进行了对比分析，见图4。脉动压力测点位置在机翼吸力面上中展面X/ C=0.9处，X为至导边距离。计算得到的脉动压力频谱谱型与幅值都与试验相符，在频率范围100 Hz～10 kHz，计算误差为2～7 dB。低频计算结果与试验更为吻合，高频大一些。脉动压力是流动非定常特性的重要表征，这些计算结果充分说明大涡模拟可以很好地反映流动的非定常特性。

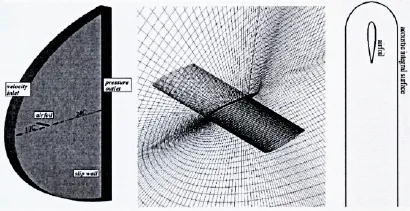
图2 机翼计算域、网格与声学积分面Fig.2 Computational domain，mesh and acoustic integral surface of airfoil

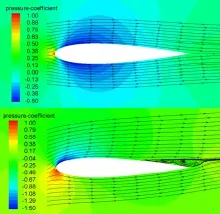
图3 中展面上机翼流场计算结果Fig.3 Computed flow field of airfoil in mid-span plane

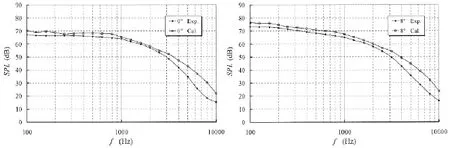
图4 机翼表面脉动压力计算结果与试验对比（左：0°；右：8°）Fig.4 Comparison between the computed pressure fluctuations and measurement(left:0°;right:8°)

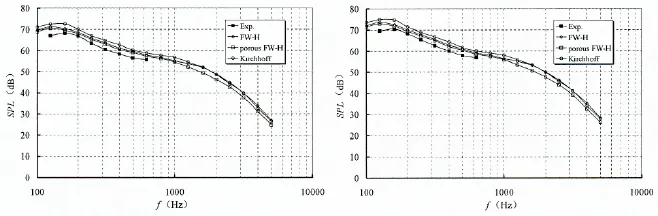
图5 机翼流激噪声计算结果与试验对比（左：0°；右：8°）Fig.5 Comparison between the computed flow induced noise and measurement(left:0°;right:8°)

流经机翼的非定常流动会产生宽带噪声，这是边界层与机翼表面相互作用将流体动能转化为声能的结果。在文献[33]中，只给出了流激噪声低频（＜1 kHz）测试结果，即导边噪声测试结果。图5将三种方法计算得到的流激噪声与试验结果进行了对比，可见谱型与幅值都计算得较好，在100～630 Hz，FW-H方法计算误差为1.8～4.1 dB；渗流FW-H方法计算误差为1.1～3.4 dB；Kirchhoff方法计算误差为3.2～5.4 dB。当频率增加时，计算得到的流噪声幅值随频率衰减趋势和以往测试结果是吻合的，符合声学一般规律。从图5的计算结果可知，由于大涡模拟准确计算了声源，所以三种方法的计算结果差异不明显，都可以给出令人满意的预报结果，这与前面数学分析吻合。表1中给出了三种流激噪声计算方法的比较，归一化时间以FW-H方法所用时间为基准进行相除得到，可见渗流FW-H方法的计算效率最高，与以往常用的FW-H方法相比，由于不再计算体积分，所以可以节省约三分之二计算时间，大大加快了研究进度。

表1 三种流激噪声计算方法比较分析Tab.1 Analysis on the three prediction approaches for flow induced noise

4.2 Powell涡声方程与FW-H声学类比方程的计算结果比较

文献[28]中曾用大涡模拟结合Powell涡声方程对于翼柱组合体的流激噪声进行了计算预报，本节在前面研究的基础上，进一步将FW-H方程的计算结果与Powell涡声方程的计算结果进行了对比分析。为了节省篇幅，流动涡旋结构计算结果不再重复给出，有兴趣的读者可以参见文献[28]。

法国研究人员所构建的翼柱组合体流激噪声基准检验试验模型由一个圆柱和一个NACA0012机翼组成。圆柱直径0.01 m，展长0.3 m，机翼弦长0.1 m，展长0.3 m，机翼放置在圆柱之后一倍弦长的地方，机翼导边距离圆柱中心0.105 m。这个试验设计的目的在于通过圆柱尾流的卡门涡街撞击机翼形成相互干扰而产生一种复杂流场，从而在远场产生声辐射，且声辐射频谱中既有窄带的谐音峰又有宽带噪声分量，不但边界层、流动分离、涡旋结构等常见的流动现象在此试验中都有出现，而且常见的流激噪声谱型在此试验中也都出现了。研究者在里昂中央大学的消音风洞中进行了流动辐射噪声测量，获得了翔实而可靠的试验数据，对于校核CFD数值计算方法发挥了巨大的作用，试验测试细节请参见文献[34]。

本文对于上述圆柱/机翼组合体的流激噪声进行计算，比较FW-H声学类比方程与P-owell涡声方程的计算能力。计算域纵向2.8 m，垂向2.4 m，侧向0.3 m，前方为速度入口，后方为压力出口，两侧为对称面。计算模型网格见图6，全域都为结构化网格，网格数量为579万。风速与试验保持一致为72 m/s。计算结果见图7与表2，表2中St表示斯特洛哈尔数。空气中参考声压为20 μPa。

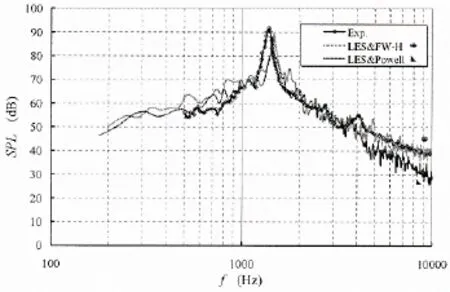
图7 圆柱/机翼组合体流激噪声计算与试验对比Fig.7 Comparison between computed flow induced noise and measurement of rod-airfoil

表2 谐音峰的幅值与频率计算验证Tab.2 Validation of the computed magnitude and frequency of the tone

表2给出了谐音峰的计算准确度，可以看到，LES结合Powell涡声方程对于谐音峰幅值、频率、St的计算误差分别为：-4.2 dB、5.3%、5.2%；LES结合FW-H声学类比方程对于谐音峰幅值、频率、的计算误差分别为：-2.8 dB、6.7%、6.8%，计算效果是令人满意的，两种方法的计算效果相当。图7给出了计算得到的远场声辐射频谱与试验结果的比较。从图中可知，LES结合Powell涡声方程计算得到的宽带噪声谱型及幅值与试验结果吻合得较好，在800 Hz～1.18 kHz频段以及1.7～3.4 kHz频段，计算结果与试验结果吻合得非常好，差异在1～3 dB，在4 kHz以上的高频频段，计算准确度有所下降，幅值误差最大可达10 dB；LES结合FW-H声学类比方程计算得到的宽带噪声谱型与幅值也令人满意，在

1.3 kHz以下以及1.6～1.9 kHz两个频段，计算准确度比Powell涡声方程略有下降，在2 kHz以上的高频频段，计算结果与试验结果吻合很好，幅值误差基本小于5 dB。经综合分析可知两种流激噪声预报方法的计算准确度是基本相当的。

作者随后又采用FW-H声学类比方程对文献[28]中方腔流激噪声进行了计算，并与文献[28]中 Powell涡声方程计算结果进行了对比，同样为了节省篇幅，流动涡旋结构计算结果不再重复给出，有兴趣的读者可以参见文献[28]。方腔长0.5 m，宽0.3 m，深0.15 m，布置在载体上，载体长4 m，宽0.8 m，厚0.3 m，首尾及两侧光顺过渡。孔中心距离载体艏部2.25 m。试验水速5 m/s，当地雷诺数Re=1.12×107。流激噪声计算结果用等效声源级表达，与试验保持一致。载体总长为L，计算域大小为载体首部向前1L，尾部向后2L，侧边界距离载体表面1L，前方为速度入口，后方为压力出口。方腔计算模型网格见图8，全域都为结构化网格，网格总数为710万。流激噪声计算结果见图9。水中参考声压为1 μPa。

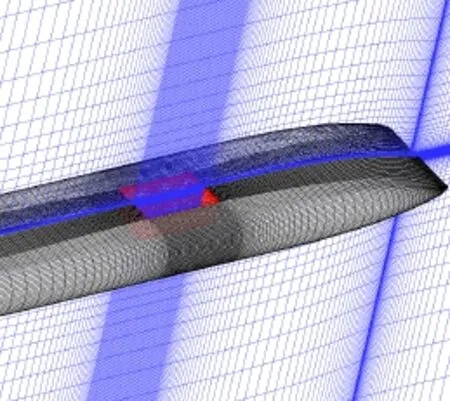
图8 方腔模型计算网格Fig.8 Computational mesh of cavity

从图9可以看到，FW-H声学类比方程和Powell涡声方程计算得到的方腔流激噪声频谱谱型及幅值都与试验吻合较好，应该说二者计算准确度相近。FWH声学类比方法的计算误差在1.3～3.9 dB，Powell涡声方程的计算误差为2.0～6.8 dB。从前面的分析可以知道，FW-H方程与Powell涡声方程本质上是一致的，差别仅在于方程右边的源项表达形式不一样，FW-H方程右边为单极子、偶极子、四极子声源，而Powell涡声方程右边为涡量与速度矢量积形成的声源，通过本文的研究可以看到，在工程预报领域，使用FW-H方程与Powell涡声方程都是可以的，但是FW-H方程是从流动模拟中获得脉动压力、速度、剪应力去重构声源，而Powell涡声方程是从流动模拟中获得涡量和速度再进行矢量相乘去重构声源，涡量是将三向速度对空间求导数再组合得到的，对于网格形式与疏密程度比较敏感。

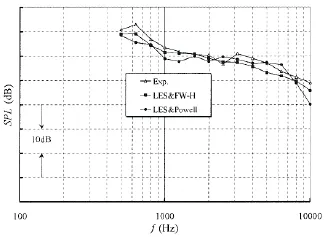
图9 方腔模型流激噪声计算与试验对比Fig.9 Comparison between computed flow induced noise and measurement of cavity

4.3 声学积分面的影响性研究

声学积分边界的选择是一件慎重的事情。从理论上讲，只要声学积分区域能将所有的涡旋发声区域都包括在内，则积分边界布置在任何地方都是可以的。然而，从CFD数值模拟的角度讲，这样做是不合适的。这是因为在数值模拟中，计算区域不可能取无穷大，进口与出口边界总是取在有限范围内，就相当于将物理真实空间人为截断，然后再在上面施加人为的边界条件，因而计算区域出口边界处的速度场会发生畸变，亦即涡发生了非物理的畸变，如果声学积分区域也将计算出口包括进来，则这种非物理的畸变会成为“伪声源”，对声学求解产生干扰。因而，我们所选择的声学积分区域通常都比实际的流动模拟区域要小，声学出口边界一般要布置在CFD流动计算出口边界上游，至于积分边界的几何形式与大小则是从源项计算以及大量的实际效果评估中得出的。如果声学计算边界将非定常流动的尾流区域截断，则会引起虚假声源[35]，对声计算产生干扰，特别当尾流是强烈的湍动涡流时更是如此。国外研究人员在计算喷流噪声时，发现了这一现象，为了解决这一问题，他们采用模态展开的办法使得声源项向声学计算域下游慢慢衰减，到达下游边界时，衰减到零，经研究发现这种方法不太适用于除喷流之外的其他情况。本文则采用斯坦福大学的研究人员所创立的一种简单实用的声学积分边界修正（boundary correction）方法[35]。

本文所计算的潜艇围壳模型长2 m，高0.83 m，厚0.195 m。流激噪声试验在中国船舶科学研究中心的循环水槽中进行，测试了不同流速下的流激噪声。本文对于水速V=4 m/s、6 m/s、8 m/s下的围壳流激噪声进行了计算，并将计算结果与试验结果进行对比，特别探讨了声学积分面对计算结果的影响。围壳计算域和网格以及声学积分面见图10。全计算域都采用结构化网格离散，网格总数为1 020万。基于围壳长度的雷诺数范围为Re=8×106～1.6×107。

图10 围壳计算域、网格与声学积分面Fig.10 Computational domain,mesh and acoustic integral surface of sail

为了能够清晰说明问题又不造成过大的计算量，本文在计算声源变化的基础上指定了a1、a2、a3、a4四个矩形平面作为声学积分面，这四个积分面的选定也参考了以往的计算经验，四个积分面所围成的长方体区域即为主要的声源区域，积分面通过程序指定，并不需要在建模与划分计算网格时预先设置，就是说这些积分面为虚拟渗流面，并不是水动力计算中常用的交接面。交接面在舰船与潜艇水动力计算中广泛采用，其主要用于复杂物体建模，当几个区域的网格形式与网格数量都不相同时，可以使用交接面进行搭接，从而大大简化建模与网格剖分的难度，提高建模效率，特别是在船/桨干扰数值模拟并进行自航性能评估时，更是要经常使用交接面将静止区域与螺旋桨转动区域搭接，并结合滑移网格技术，完成螺旋桨运转的模拟。交接面方法的缺陷就在于其两侧的流动通量并不相同，所以流谱在交接面上会出现阶跃，实际计算中往往结合数值强制方法使得流量尽可能相同，但并不能根本解决这一问题，所幸的是这种阶跃对于积分水动力（阻力、推力、扭矩）的数值模拟影响很小，由此产生的计算误差基本可以忽略，因此可在水动力计算中采用。但是，交接面两侧的流动阶跃有时却会显著影响脉动量的计算，引起计算误差，会对脉动压力和流激噪声计算结果造成影响，所以在流激噪声计算中一般不推荐采用交接面这种方式，如果要使用，则要通过数值手段抑制其本身的干扰噪声。本文利用虚拟渗流面结合FW-H方程不但能保证计算精度，而且可以大为提高计算效率，前面已做了详细介绍。计算结果见图11～12与表3。表3中取水速4 m/s时的试验测量值为A，其他值在A的基础上再加一变化量，用此形式给出。

由图11可知，当流速V=6 m/s时，如果将a1、a2、a3与a4这四个表面全部作为声源积分面，则计算出的声压谱在3 kHz以下的幅值与谱型都与试验比较接近，但在3 kHz与8 kHz两个频率附近却出现两个明显的峰值，这就是所谓的虚假噪声，由于a1、a4两个积分面与主流方向垂直，所以这两处的虚假噪声就是由于主流撞击a1、a4两个积分面或者说a1、a4两个积分面将主流人为截断造成的。从表3可知，选择a1、a2、a3与a4作为积分面时，总声级计算误差为7.6 dB。从工程评估角度来看，流激噪声谱型、幅值与总声级的计算结果显然是不能令人满意的。

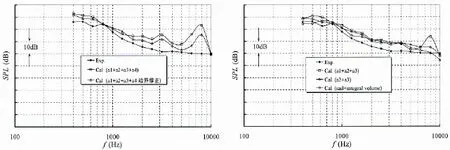
图11 围壳流激噪声计算结果与试验对比（V=6 m/s）Fig.11 Comparison between computed results of sail flow induced noise and measurement(V=6 m/s)

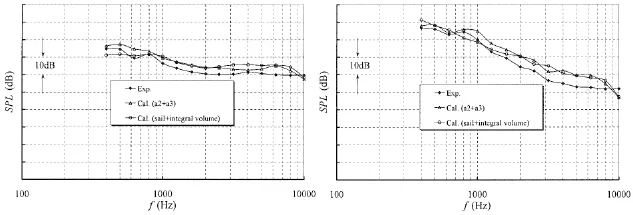
图12 围壳流激噪声计算结果与试验对比（左：V=4 m/s；右：V=8 m/s）Fig.12 Comparison between computed results of sail flow induced noise and measurement（left:V=4 m/s;right:V=8m/s）

表3 声源积分面对围壳流激噪声总声级计算结果的影响（400 Hz～10 kHz，dB）Tab.3 The influence of acoustic integral surface on the computed OASPL of sail flow induced noise(400 Hz～10 kHz,dB)

由图11可知，如果将a1、a2、a3与a4这四个表面全部作为声源积分面，并同时采用边界修正方法，可以看到虚假噪声得到一定程度的抑制，幅值减小3～7 dB，但是两个明显的峰值仍然存在，并没有消除，就是说边界修正方法并不能根本解决虚假噪声的问题。

由于面a4位于围壳尾流中，下面将面a4舍弃，只取a1、a2、a3作为声源积分面，则由图11可知，第一个（3 kHz）虚假噪声峰值消失，第二个（8 kHz）虚假噪声峰值也减小了9 dB，但仍然显著存在，频率在6 kHz以下的谱型与幅值与试验结果较接近，总声级计算误差为4.7 dB。再将a1、a4同时舍弃，只取a2、a3作为声源积分面，由图11可知，两个虚假噪声峰值全部消失，声压谱谱型与幅值的计算结果都与试验结果比较接近，频谱幅值计算误差为1.4～6.5 dB，总声级计算误差为2.9 dB。

经分析可知，选择与主流平行的a2、a3面作为声学积分面是合适的。利用虚拟渗流面方法不但可以准确计算偶极子与四极子声源，而且仅需要计算面积分，不需要计算体积分，计算效率很高。如果选择围壳表面作为积分面，同时计算声源区域中的四极子体积分，则计算结果如图11所示，谱型与幅值的计算结果也都与试验结果比较接近，频谱幅值计算误差为1.8～6.9 dB，总声级计算误差为2.1 dB。计算结果也是令人满意的，只是计算时间要比前面渗流面方法延长两倍以上。因此，在本文的潜艇围壳流激噪声计算中，选择a2、a3两个渗流面求取FW-H方程的渗流解或者选择围壳表面和声源体求取FW-H方程的原初解都是可以的，从声学计算角度判断可知二者计算精度基本相同，主要区别在于计算效率。

下面就采用上述两种方法对于水速V=4 m/s和V=8 m/s情况下的围壳流激噪声进行了计算，如图12所示。可见两个流速下声压谱计算结果都与试验比较吻合。V=4 m/s时，a2、a3渗流面方法得到的声压谱幅值计算误差为1.3～5.7 dB，总声级计算误差为2.8 dB；围壳表面加体积分方法得到的声压谱幅值计算误差为1.4～5.6 dB，总声级计算误差为2.2 dB。V=8 m/s时，a2、a3渗流面方法得到的声压谱幅值计算误差为1.4～6.9 dB，总声级计算误差为2.4 dB；围壳表面加体积分方法得到的声压谱幅值计算误差为1.5～7.1 dB，总声级计算误差为1.8 dB。计算结果能够满足工程评估要求。

5 结 语

流/声耦合是流体力学与声学的交叉学科，该领域的研究需要繁难的数值计算和精细的试验验证，技术难度大。复杂流动与流激噪声的计算与试验研究是流声耦合领域的重要课题，也是长期困扰水动力学界的一大难题，计算与试验研究都具有很大的挑战性，其学术研究意义和工程实用价值已经得到国际上的普遍公认。本文主要对于FW-H声学类比方法、渗流FW-H声学类比方法、Kirchhoff方程与Powell涡声理论的物理内涵、数学公式和计算效果进行了分析比较，探讨了声学积分面的影响，并与风洞和水槽试验结果进行了对比，进一步证明计算方法切实可行，计算量级可靠。目前在使用渗流FWH声学类比方法时，积分面的选择虽然是在计算声源变化的基础上得到的，但具体形式还是参照了大量计算对比中积累的经验，将来可以从物理概念和数学内涵入手进行研究，争取能够找到普适性的规律，即积分面几何形式及尺寸与物理问题之间的明确关系，从而减少巨大的工作量，为实用设计服务。本文得到的主要结论如下：

（1）从工程预报角度来看，渗流FW-H声学类比方法计算准确度好，计算效率高，Powell涡声方程的计算效果也较好，二者都是工程实用的流激噪声预报方法；

（2）使用渗流FW-H声学类比方法时，合理选择声学积分面（几何形式、大小、位置）是正确计算流激噪声的关键。积分面的选择首先要考察声源项的变化，其次要从大量计算对比中积累经验得到，要非常慎重地加以考虑，但有一点可以肯定，就是积分面不能在物体附近截断主流，否则会产生较大的虚假噪声。

[1]William K Blake.Mechanics of flow-induced sound and vibration[M].Academic Press.INC,New York,1986.

[2]Crighton D G,Dowling A P,Ffowcs Williams J E,et al.Modern methods in analytical acoustics[M].Springer-Verlag London Limited,1992.

[3]Ross D.Mechanics of underwater noise[M].Peninsula Publishing,Los Altos,California,U.S.A.,1987.

[4]Skelton E A,James J H.Theoretical acoustics of underwater structures[M].Imperial College Press,1997.

[5]Wang M,Jonathan B,Freund,Lele S K.Computational prediction of flow-generated sound[J].Annu.Rev.Fluid Mech, 2006,38:483-512.

[6]汤渭霖.水下噪声学原理[G].上海:上海交通大学讲义,2004.

[7]朱锡清.船舶流体动力噪声原理[G].无锡:中国船舶科学研究中心讲义,2006.

[8]何祚镛.水下噪声及其控制技术进展和展望[J].应用声学,2002,21(1):26-34. He zuoyong.Review of some aspects of underwater noise including its control techniques and its prospect[J].Applied Acoustics,2002,21(1):26-34.

[9]魏以迈.我国船舶水下噪声研究进展综述[J].上海造船,2000,1:27-32. Wei Yimai.The progress of the researches on the marine underwater noise in China[J].Shanghai Shipbuilding,2000(1): 27-32.

[10]俞孟萨,吴有生,庞业珍.国外舰船水动力噪声研究进展概述[J].船舶力学,2007,11(1):152-158. Yu Mengsa,Wu Yousheng,Pang Yezhen.A review of progress for hydrodynamic noise of ships[J].Journal of Ship Mechanics,2007,11(1):152-158.

[11]李太宝.计算声学声场的方程和计算方法[M].北京:科学出版社,2005.

[12]Wagner C,Huttl T,Sagaut P.Large eddy simulation for acoustics[M].New York:Cambridge University Press,2007.

[13]Lighthill M J.On sound generated aerodynamically.Part I.General Theory[J].Proc.R.Soc.London Ser,A 211,1952: 564-587.

[14]Curle N.The influence of solid boundaries on aerodynamic sound[J].Proc.Roy.London Soc.231A,1955:1187,505-514.

[15]Ffowcs Williams J E,Hawkings D L.Sound generation by turbulence and surfaces in arbitrary motion[J].Proc.Roy.Soc. London,264 A,1969:321-342.

[16]Goldstein,M.Unified approach to aerodynamic sound generation in the presence of sound boundaries[J].J Acouts.Soc. Am.,1974,56:497-509.

[17]Powell A.Theory of vortex sound[J].J Acoust.Soc.Am.1964,36(1):177-195.

[18]Howe M S.Contributions to the theory of aerodynamic sound with application to excess jet noise and the theory of the flute [J].J Fluid Mech,1975,71:625-673.

[19]Howe M S.Theory of vortex sound[M].New York:Cambridge University Press,2003.

[20]张 楠,沈泓萃,姚惠之,朱锡清,俞孟萨.孔穴流激噪声的计算与验证研究[J].船舶力学,2008,12(5):799-805. Zhang Nan,Shen Hongcui,Yao Huizhi,Zhu Xiqing,Yu Mengsa.Validation and calculation of flow-induced noise of cavity[J].Journal of Ship Mechanics,2008,12(5):799-805.

[21]张 楠,沈泓萃,朱锡清,姚惠之,谢 华.三维孔腔流激噪声的大涡模拟与声学类比预报与验证研究[J].船舶力学, 2010,14(1):181-190. Zhang Nan,Shen Hongcui,Zhu Xiqing,Yao Huizhi,Xie Hua.Validation and prediction of flow induced noise of 3-dimensional cavity with large eddy simulation and acoustic analogy[J].Journal of Ship Mechanics,2010,14(1):181-190.

[22]Zhang Nan,Shen Hongcui,Yao Huizhi.Numerical investigation of the flow induced noise of submarine[C]//8th International Conference on Hydrodynamics(ICHD2008),September 30-October 3,2008.Nantes,France,2008:591-599.

[23]Zhang Nan,Shen Hongcui,Yao Huizhi.Numerical simulation of cavity flow induced noise by LES and FW-H acoustic analogy[J].Journal of Hydrodynamics,2010,22:242-247.

[24]张 楠,沈泓萃,朱锡清,姚惠之.基于大涡模拟和Kirchhoff积分的孔腔流动发声机理分析[J].船舶力学,2011,15 (4):427-434. Zhang Nan,Shen Hongcui,Zhu Xiqing,Yao Huizhi.Analysis of the mechanism of cavity flow induced noise with large eddy simulation and Kirchhoff integral[J].Journal of Ship Mechanics,2011,15(4):427-434.

[25]张 楠.孔腔流动和流激噪声机理及耦合计算方法研究[D].无锡:中国船舶科学研究中心,2010.

[26]Zhang Nan,Lü Shijin,Xie Hua.Numerical simulation of unsteady flow and flow induced sound of airfoil and wing/plate junction by LES and FW-H acoustic analogy[C]//The 2nd international conference on advances in computational modeling and simulation.Kunming,China,2013.(Applied Mechanics and Materials,2014:444-445,479-485).

[27]张 楠,吕世金,沈泓萃,谢 华.潜艇围壳线型优化抑制脉动压力与流激噪声的数值模拟研究[J].船舶力学,2014, 18(4):448-458. Zhang Nan,Lü Shijin,Shen Hongcui,Xie Hua.Numerical simulation on the effect of fairwater optimization to suppressthe wall pressure fluctuations and flow induced noise[J].Journal of Ship Mechanics,2014,18(4):448-458.

[28]张 楠,李 亚,王志鹏,王 星,张晓龙.基于LES与Powell涡声理论的孔腔流激噪声数值模拟研究[J].船舶力学, 2015,19(11):1393-1408. Zhang Nan,Li Ya,Wang Zhipeng,Wang Xing,Zhang Xiaolong.Numerical simulation on the flow induced noise of cavityby LES and Powell vortex sound theory[J].Journal of Ship Mechanics,2015,19(11):1393-1408.

[29]Zhang Nan,Xie Hua,Wang Xing,Wu Baoshan.Computation of vortical flow and flow induced noise by large eddy simulation with FW-H acoustic analogy and Powell vortex sound theory[J].Journal of Hydrodynamics,Ser:B,2015,28(2): 255-266.

[30]Brentner K S,Farassat F.Analytical comparison of the acoustic analogy and Kirchhoff formulation for moving surfaces[J]. AIAA Journal,1998,36(8):1379-1386.

[31]Germano M,Piomelli U,Moin P,Cabot W H.A dynamic subgrid-scale eddy viscosity model[J].Phys.Fluids A,1991,3 (7):1760-1765.

[32]Lilly D K.A proposed modification of the Germano subgrid-scale closure method[J].Physics of Fluids,1992,4(3):633-635.

[33]William J Devenport,Joshua K Staubs,Stewart A L Glegg.Sound radiation from real airfoils in turbulence[J].Journal of Sound and Vibration,2010,329:3470-3483.

[34]Marc C Jacob,Jerome Boudet,Damiano Casalino,MarcMichard.A rod-airfoil experiment as benchmark for broadband noise modeling[J].Theoret.Comput.Fluid Dynamics,2005,19:171-196.

[35]Meng Wang,Sanjiva K Lele,Parviz Moin.Computation of quadrupole noise using acoustic analogy[J].AIAA Journal, 1996,34(11):2247-2254.

[36]Di Francescantonio P.A new boundary integral formulation for the prediction of sound radiation[J].Journal of Sound and Vibration,1997,202(4):491-509.

Research on numerical simulation approach for flow induced noise and the influence of the acoustic integral surface

ZHANG Nan,WANG Xing,XIE Hua,LI Ya
(a.National Key Laboratory of Hydrodynamics;b.National Key Laboratory on Ship Vibration and Noise, China Ship Scientific Research Center,Wuxi 214082,China)

Study on the complicated flow field and flow induced noise of underwater vehicle has obvious theoretical meaning and practical significance in flow-acoustic coupling domain.In this paper,four prediction approaches for flow induced noise including FW-H acoustic analogy,porous FW-H acoustic analogy,Kirchhoff equation and Powell vortex sound theory are analyzed and compared with each other.The flow induced noise of three-dimensional NACA0015 airfoil,rod-airfoil and cavity are computed by LES with the four approaches.And,the numerical simulations are validated by the measurements.The accuracy and efficiency of the four acoustic calculation approaches are studied.Finally,the flow induced noises of submarine sail at three velocities are predicted by the porous FW-H acoustic analogy and compared with experimental data.The tendency of sail flow induced noise under different velocities is analyzed and the influence of acoustic integral surface is studied.

flow induced noise;large eddy simulation(LES);FW-H acoustic analogy;porous FW-H acoustic analogy;Kirchhoff equation;Powell vortex sound theory

U661.3

：Adoi:10.3969/j.issn.1007-7294.2016.07.013

1007-7294（2016）07-0892-17

2016-05-15

国家自然科学基金资助项目（51079133）；江苏省自然科学基金资助项目（BK2010162）

张 楠（1977-），男，博士，研究员，E-mail：zn_nan@sina.com；王 星（1987-），男，工程师。