静压下球形空腔吸声覆盖层的建模与性能分析
张 冲,何世平,易少强
(1.海军工程大学 动力工程学院,武汉 430033;2.海军航空兵学院91899部队,辽宁 葫芦岛 125001)
静压下球形空腔吸声覆盖层的建模与性能分析
张 冲1,2,何世平1,易少强1
(1.海军工程大学 动力工程学院,武汉 430033;2.海军航空兵学院91899部队,辽宁 葫芦岛 125001)
基于声波垂直入射下的二维理论,利用COMSOL软件建立球形空腔吸声覆盖层单元模型,得到了在空腔受压变形基础上直接进行声学性能计算的耦合模型,避免了以往根据变形量重新建模带来的误差,并与静压下穿孔率的理论公式进行对比,验证了模型的有效性;利用所建模型分析了静压下球形空腔的吸声性能,并比较了内部气压对空腔变形和吸声系数的影响。结果表明:随着静压的增大,峰值上移频带展宽,更显著的是吸声效果总体变差;内部气压使得空腔变形量减少、低频吸声效果有所提高。
吸声覆盖层;球形空腔;静压;内部气压;吸声性能;COMSOL
0 引 言
吸声覆盖层技术是水下减振降噪技术中继低噪声螺旋桨技术和浮筏技术以后的又一大技术进步[1-2],对其开展理论研究有助于更好地了解吸声覆盖层的声学特性,对工程设计具有重要的指导意义。目前对含空腔的吸声覆盖层的研究主要有解析方法、数值方法等[3-5],这些研究大都是在常压条件下进行的,没有考虑外部静水压力的影响。因此在理论计算和有限元仿真中,所得到的结果与实际测试结果存在很大差别。实际使用的吸声覆盖层是在几百米深的水下工作的,其必然要受到静水压力的作用,声学效果也会随之发生改变。静压下吸声覆盖层吸声性能发生改变的原因主要有两个方面:一是材料的动态力学性能会随着压力而变化;二是吸声覆盖层受到静水压力时,空腔会发生形变。对于材料力学性能的研究,国内外许多学者针对类橡胶的粘弹性材料进行了很多测试和分析。吕林海[6]利用动态黏弹谱仪对高分子聚合物力学性能的频变特性进行了测试,并基于得出的动态力学参数计算了圆柱形空腔吸声覆盖层的声学性能;黄修长等[7]利用声管测试的方法对材料的参数进行了测试,分析了各参数对谐振型吸声结构的影响;邹明松等[8]采用传递矩阵法建立了静压下吸声覆盖层的声阻抗求解方法。而对于吸声覆盖层空腔变形的研究还处于起步阶段,姜闻文等[9]利用ANSYS软件对几种橡胶结构的吸声覆盖层在静压下的吸声性能进行了研究,比较了不同结构的空腔对吸声性能的影响;Panigrahi等[10]基于有限元法对不同组合空腔在静压下的声学性能进行了计算,并将结果与解析解、实验作了对比分析;陶猛[11]推导出了吸声覆盖层声学特能的简化计算方法,计算了不同静压下吸声覆盖层的声学性能。
当前的文献研究都是基于有限元法,首先计算静压下吸声覆盖层单元的几何变形,然后根据变形量重新建立规则形状的吸声覆盖层单元模型。由于空腔在静压下的变形是无规则、无规律可循的,即使得到静压下的变形量,二次建模时也很难与实际的空腔变形相吻合,这对后续的声学性能分析带来一定的误差;另一方面,关于静压下吸声覆盖层的所有研究都没有考虑空腔内部气压的影响。本文鉴于以上两方面的不足,利用COMSOL软件建立了球形空腔的固体力学和声—固耦合模型,然后在空腔受压发生形变的模型上直接划分网格,计算不同压力下吸声覆盖层的吸声性能,避免了二次建模;并进一步分析了静压下空腔内部气压对吸声性能的影响。
1 物理模型
1.1 有限元物理模型的建立
具有球形空腔周期性分布的吸声覆盖层结构如图1所示,在粘弹性体内有成正三角形排列的相互平行的球形空腔。把整个吸声覆盖层看成是由各个以球形空腔为中心的正六棱柱体组成,由于结构对称、重复,只需要研究其中一个棱柱体中的波传播即可。然而要建立一个六面棱柱体的理论模型,是一件相当困难的事情。为了计算简便,本文通过几何转换用圆柱体近似代替六棱柱体[12],每个吸声覆盖层单元就可以简化为一段有限长粘弹性圆柱管。吸声覆盖层中波的传播与损耗问题可以模型化为粘弹性圆柱管中波的传播与损耗,这为建立理论模型提供了极大的方便。
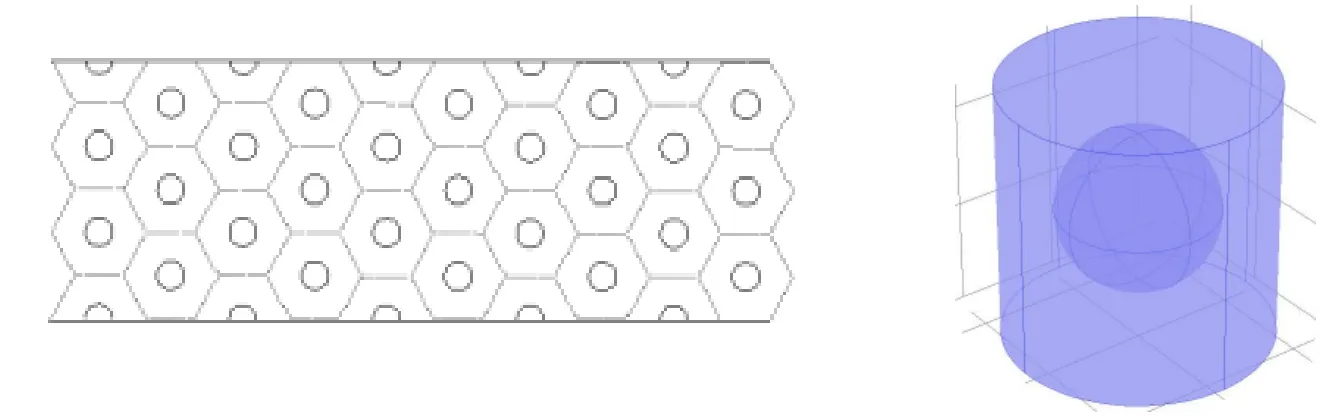
图1 球形空腔周期性分布的吸声覆盖层结构Fig.1 The structure of the absorbing layer of the periodic distribution of the spherical cavities
三维周期边界条件下的有限元模型虽然能完整地仿真吸声覆盖层的声学特性,但由于三维模型的体单元节点数过多会造成单次运算效率较低,难以满足多次迭代运算需求。考虑到吸声覆盖层单元具有轴对称性,因此在建模时将体单元模型(三维周期边界模型)简化为面单元模型(二维轴对称模型),如图2所示。
图2左侧边界处、上下两端均超出有限元的虚线是模型的旋转中心轴,有限元模型仅为完整单元的一个旋转截面。灰色区域W、V分别代表入射端水介质、橡胶覆盖层基体,空白区域C代表球形空腔。吸声覆盖层模型的边界1为固定边界;三维模型的周期性边界条件转化为二维轴对称模型的法向量位移为0的边界(即边界2、3);边界4、5、6为模型的轴对称边界;在有限元模型中通过设置声—固耦合边界(即边界7)来处理水介质—橡胶基体的耦合作用;通过设置吸收边界9解决无限水介质区域,即在W外端面法向方向添加平面波辐射条件,使有限厚度的有限元能代表无限厚的水介质;边界8为球形空腔的自由边界。
声波从上端面沿旋转轴方向垂直入射模型单元,会产生声波的反射、折射、辐射、吸收等作用。通过积分入射声波、吸收声波的能量可求得吸声覆盖层在声波垂直入射条件下的吸声特性。
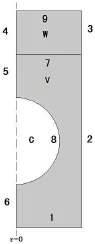
图2 吸声覆盖层的单元模型Fig.2 The unit cell of anechoic coatings model
1.2 模型的有效性验证
圆柱形空腔的吸声覆盖层有限元模型比较成熟,陶猛[13]、谭洪波等[14]已多次验证了其有效性,但对球形空腔单元受压后直接计算其吸声性能的模型还没验证过其可行性。Gaunaurd[15]理论分析了受压前后球形空腔吸声覆盖层的穿孔率与静水压力的关系,

式中:μ是材料的剪切模量,P代表静水压力,Φ代表穿孔率。
本文正是利用(1)式穿孔率的理论模型与COMSOL有限元模型作对比,以验证模型的可行性。在如图2所示的模型中,穿孔率可以表示为

式中:Vc(P)、Vv分别表示静压P下球形空腔的体积、橡胶基体的体积。
要证明模型的有效性,只要验证(1)式、(2)式中的Φ是否相同即可。但在静压P下Vc(P)是变化的,要想计算Vc(P),必须借助于Stokes公式(3)将曲面积分转化为曲线积分

在图示的二维轴对称模型中,主要是对空腔内表面进行曲线积分,

式中:Asphere代表球形空腔的曲线积分,z代表球形空腔内表面每一点的z向坐标,nz代表z坐标的法向矢量,lsphere代表球形空腔的曲线。
得到空腔内表面的曲线积分后,再通过COMSOL中的“计算旋转几何的积分”选项就可以将求得的Asphere转化为球形空腔受压后的体积,即Vc(P)。在计算时橡胶基体的泊松比在0.499左右,为几乎不可压缩材料,故Vv是定值。
在验证计算时,采用的橡胶材料的参数是随频率的改变而发生变化的,参数表达式根据实验数据拟合得到[16],橡胶材料的杨氏模量(单位:Pa)、损耗因子和泊松比的表达式为:
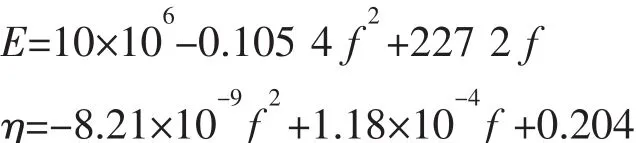
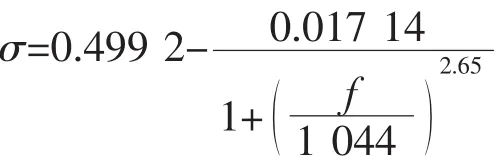
由于橡胶的杨氏模量为复杨氏模量,只要知道复杨氏模量的实部E和虚部η就可以求得复杨氏模量,故可表示为:
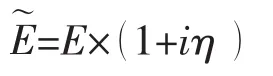
以上各式中,f代表频率,i代表虚数。
COMSOL有限元与解析公式通过计算得到的结果如图3所示。从图中可以看出,有限元与解析解的穿孔率变化曲线吻合较好。至于在静压较大时,有限元结果与解析公式的穿孔率存在一定的差别,主要是由于解析公式在推导的过程中,假设计算单元中含有均匀分布的小气泡,而且气泡在受压变形后仍是规则的球形,故理论推导的假设与空腔受压后呈椭球形的实际变形存在误差。
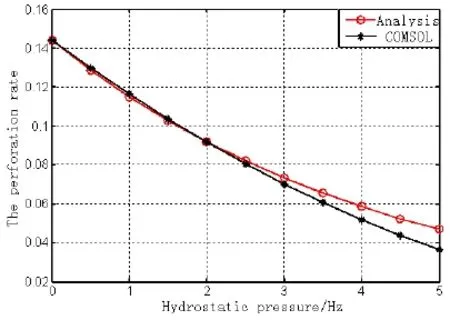
图3 有限元与理论结果比较图Fig.3 Comparison of FEM and theoretical results
2 不同压力下吸声覆盖层的形变及吸声性能
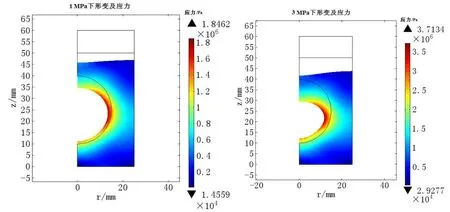
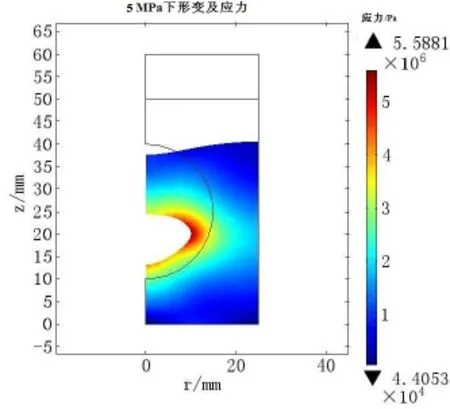
图4 不同静压下单元形变及应力图Fig.4 Deformation and stress of unit under different hydrostatic pressure
与目前静压下吸声覆盖层有限元研究不同,本文在利用COMSOL建模时,选用“固体力学”、“声—固耦合”和“移动网格”三大模块相结合,主要好处是单元模型在计算静压变形后,可以依靠“移动网格”直接将计算的变形应用于声—固耦合计算中,不需要根据变形量二次建模,有效地提高了计算精度。如图4所示为1 MPa、3 MPa和5 MPa下的静压变形,吸声覆盖层的声学特性的计算就是在此变形基础上直接进行的。从图中可以看出,吸声覆盖层随着压力的增大,球形空腔的形变量和覆盖层厚度的压缩量越大,且应力能越大。
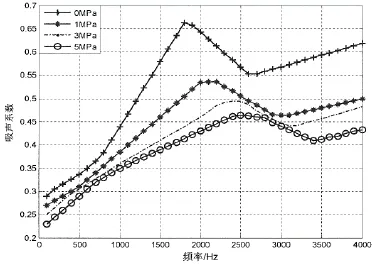
图5 不同静压下的吸声系数曲线Fig.5 Absorption coefficient curves under different hydrostatic pressure
图5比较了吸声覆盖层在不同静压下的吸声系数,可以看出,随着静压的增大,吸声系数总体呈下降趋势,低频吸声性能变差,且峰值向高频移动,频带增宽100 Hz左右。从共振理论分析看,由于空腔体积和覆盖层厚度被压缩,等效阻抗失效,反射增强,使得共振峰上移频带展宽,而且低频吸声效果随之下降。目前许多学者研究的圆柱形空腔,虽然表明在静压下吸声峰值发生移动,但在高频段静压越大吸声系数也越大[9],即压力大的吸声系数曲线要穿透压力小的曲线有上扬的走向。而本文研究球形空腔却发现,吸声系数曲线随着压力的增大总体呈下降趋势(如在5 MPa时,吸声系数比常压,即0 MPa时,总体下降高达近30%),这一点与先前学者研究的圆柱形空腔存在显著的差异。
球形空腔与圆柱形空腔虽然结构不同,但吸声系数走向不会发生太大的不同,趋势应该一致[17]。所以COMSOL计算结果与其他学者研究的结论存在差别的主要原因是:由于单元模型在静压下的变形呈不规则椭球形(图4所示),如若用计算的变形量重新建立模型,不可能与实际变形相对应;本文在计算声学特性时,单元采用的是受压变形后的实际模型,避免了以往根据变形量重新建模的误差,而这种不规则的形变造成了对声波吸收能力的减弱、对声波反射能力的增强,故计算的吸声系数总体下降。同时,从工程设计方面表明,若仅仅要求常压(即无静压作用)下设计的吸声覆盖层满足工程需要,那么在水下使用时会达不到想要的吸声效果,因为在水下不仅吸声频带发生变化,吸声性能也会明显地减弱。
3 静压下空腔内部气压的影响
无论圆柱形空腔还是球形空腔,内部不是真空,都是充满空气的。吸声覆盖层在静压作用下被压缩,空腔体积会缩小,内部气体压力会随之增大。那么静压下,空腔内部气压会对吸声覆盖层的形变和吸声性能产生怎样的影响,至今没有相关文献对此进行过研究。本文在利用COMSOL有限元建模时,把内部气压的作用考虑在内,分析其对单元形变和吸声系数的影响。
受压前、后空腔内气体压力存在如下关系:

式中:p0、p分别代表压缩前、后空腔内的压强,ρ0、ρ分别代表压缩前、后空腔内空气的密度,A0、A分别代表压缩前后二维球形空腔的面积,γ代表气体常数。其中,p0=0.1 MPa是标准大气压力,γ=1.4。
随着压力的增加,就会有剩余的空气压力作用在空腔内壁,对空腔形变产生一定的作用。由(5)式可知,剩余的空气压力为:

在COMSOL模型中,将△p作为边界载荷加载在空腔内壁上。图6和图7所示分别为有、无空气压力作用下,空腔体积的减少量相对于原空腔体积的变化率和静压为5 MPa时吸声系数曲线。
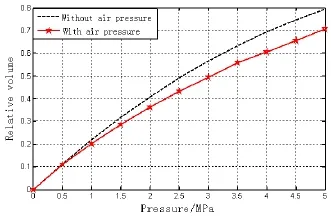
图6 相对体积变化率Fig.6 Relative volume change rate curves

图7 吸声系数曲线比较图Fig.7 The comparison of absorption coefficient curves
通过相对体积比较图可以看出,在空腔内部,有空气压力的变形量要比无空气压力的变形量小,原因是空腔受到静压压缩时,内部气体会给空腔壁沿着法向向外作用的支撑力,以阻碍空腔的压缩变形。通过吸声系数比较图可以看出,在低频段(1 600 Hz以下频段),有空气压力的吸声系数要大于无空气压力的吸声系数,高频段正好相反。这是因为无空气压力的孔腔被压缩量大,吸声覆盖层基体上部的等效阻抗不再是渐变的,与水阻抗失配的增加,使得反射更加增强,孔腔的固有频率也会随之升高,低频吸声效果故而比有空气压力的要差,高频反而要强[18]。
4 结 语
本文基于声波垂直入射条件下吸声覆盖层的解析理论,利用COMSOL有限元软件建立静水压力下球形空腔模型,将计算的穿孔率与现有解析公式进行了对比,验证了模型的有效性,然后计算了不同静压下模型单元的变形量,并在单元形变的基础上采用移动网格模块直接计算声—固耦合的吸声系数,最后讨论了空腔内部气压对空腔形变和吸声性能的影响。结果表明:利用移动网格直接在单元形变基础上计算吸声系数时,峰值向高频移动,频带变宽,而且与其他学者根据变形量二次建模得到的结果相比,吸声效果随着静压的增大整体呈下降趋势;内部气压的作用可以使得空腔变形量减小,低频吸声性能有所提升。
[1]孟晓宇,肖国林,陈 虹.国外潜艇声隐身技术现状与发展综述[J].舰船科学技术,2011,33(11):135-139. Meng Xiaoyu,Xiao Guolin,Chen Hong.Review of the present situation and development of acoustic stealth technology for submarines abroad[J].Ship Science and Technology,2011,33(11):135-139.
[2]苏 强,王桂波,朱鹏飞,宋 杨.国外潜艇声隐身前沿技术发展综述[J].舰船科学技术,2014,36(1):1-9. Su Qiang,Wang Guibo,Zhu Pengfei,et al.Review of foreign submarine acoustic stealth frontier technologies development[J].Ship Science and Technology,2014,36(1):1-9.
[3]汤渭霖,何世平,范 军.含圆柱形空腔吸声覆盖层的二维理论[J].声学学报,2005,30(4):289-295. Tang Weilin,He Shiping,Fan Jun.Two-dimensional model for acoustic absorption of viscoelastic coating containing cylindrical holes[J].Acta Acustica,2005,30(4):289-295.
[4]何世平,汤渭霖,何 琳,等.变截面圆柱形空腔覆盖层吸声系数的二维近似解[J].船舶力学,2006,10(1):120-127. He Shiping,Tang Weilin,He Lin,et al.Analysis of acoustic characteristics of anechoic coating containing varying sectional cylindrical cavity[J].Journal of Ship Mechanics,2006,10(1):120-127.
[5]Easwaran V,Munjal M L.Analysis of reflection characteristics of a normal incidence plane wave on resonant sound absorbers:A finite element approach[J].Journal of the Acoustical Society of America,1993,3(3):1308-1318.
[6]吕林梅,温激鸿,赵宏刚,温熙森.黏弹性材料的动态力学特性及其对覆盖层吸声性能的影响[J].物理学报,2014,63 (15):1-6. Lü Linmei,Wen Jihong,Zhao Honggang,et al.Dynamical mechanical property of viscoelastic materials and its effect on acoustic absorption of coating[J].Acta Phys.Sin.,2014,63(15):1-6.
[7]黄修长,朱蓓丽,胡 碰,华宏星.静水压力下橡胶动态力学参数的声管测量方法[J].上海交通大学学报,2013,47 (10):1503-1508. Huang Xiuchang,Zhu Beili,Hu Peng,et al.Measurement of dynamic properties of rubber under hydrostatic pressure by water-filled acoustic tube[J].Journal of Shanghai Jiaotong University,2013,47(10):1503-1508.
[8]邹明松,吴文伟,余晓丽,廖彬彬.静水压下声学覆盖层声阻抗研究[J].舰船科学技术,2013,35(3):57-60. Zou Mingsong,Wu Wenwei,Yu Xiaoli,et al.Calculation of acoustic coating’s impedance under hydrostatic pressure[J]. Ship Science and Technology,2013,35(3):57-60.
[9]姜闻文,陈光冶,朱 彦.静水压变化下橡胶结构吸声性能的计算与分析[J].噪声与振动控制,2006(5):55-57. Jiang Wenwen,Chen Guangye,Zhu Yan.Computation and analysis of sound absorption performance of rubber structures under variable hydraulic pressure[J].Noise and Vibration Control,2006(5):55-57.
[10]Panigrahi S N,Jog C S,Munjal M L.Multi-focus design of underwater noise control linings based on finite element analysis[J].Applied Acoustics,2008,69(12):1141-1153.
[11]陶 猛,卓琳凯.静水压力下吸声覆盖层的声学性能分析[J].上海交通大学学报,2011,45(9):1340-1344. Tao Meng,Zhuo Linkai.Effect of hydrostatic pressure on acoustic performance of sound absorption coating[J].Journal of Shanghai Jiaotong University,2011,45(9):1340-1344.
[12]何世平.粘弹性圆柱管中波的传播研究及吸声覆盖层声学特性研究[D].上海:上海交通大学,2004. He Shiping.Research of wave propagation in viscoelastic tube and analysis of acoustic characteristics of anechoic coating [D].Shanghai:Shanghai Jiaotong University,2004.
[13]陶 猛,卓琳凯.基于ANSYS的吸声覆盖层声学性能计算与分析[J].振动与冲击,2011,30(1):87-90. Tao Meng,Zhuo Linkai.Simulation and analysis for acoustic performance of a sound absorption coating using ANSYS software[J].Journal of Vibration and Shock,2011,30(1):87-90.
[14]谭红波,赵 洪,徐海亭.有限元法分析空腔周期分布粘弹性层的声特性[J].声学学报,2003,28(3):277-282. Tan Hongbo,Zhao Hong,Xu Haiting.Sound characteristics of the viscoelastic layer containing periodic cavities by the finite element method[J].Acta Acustica,2003,28(3):277-282.
[15]Gaunaurd G,Callen E,Barlow J.Pressure effects on the dynamic effective properties of resonating perforated elastomers [J].J Acoust.Soc.Am.,1984,76(1):173-177.
[16]胡 碰.静水压力下声学覆盖层声学性能模块化方法研究[D].上海:上海交通大学,2008. Hu Peng.Research of acoustic coating’s properities under hydrostatic pressure by modular-FEM method[D].Shanghai: Shanghai Jiaotong University,2008.
[17]姚熊亮,刘文贺,刘庆杰,张 妍.水深与腔型对隔声去耦瓦吸声系数的影响[J].哈尔滨工程大学学报,2007,28(6): 605-610. Yao Xiongliang,Liu Wenhe,Liu Qingjie,et al.Influence of depth and cavity shape on absorption coefficients of soundisolating decoupled tiles[J].Journal of Harbin Engineering University,2007,28(6):605-610.
[18]罗 忠,朱 锡,林志驼,王卫忠.水下吸声覆盖层结构及吸声机理研究进展[J].舰船科学技术,2009,31(8):23-30. Luo Zhong,Zhu Xi,Lin Zhituo,et al.A review of underwater anechoic coating structure and absorption theories[J].Ship Science and Technology,2009,31(8):23-30.
Model and absorption performance of anechoic coating embedding sphere cavities
ZHANG Chong1,2,HE Shi-ping1,YI Shao-qiang1
(1.College of Power Engineering,Naval Univ.of Engineering,Wuhan 430033,China; 2.Unit No.91899,Naval Air Force Academy,Huludao 125001,China)
Based on the 2D theory of sound wave normally impinging on the absorption layer,the acousticsolid interaction model of anechoic coating which contains sphere cavities was made by COMSOL software and the model can calculate absorption coefficient directly instead of remodeling according to the volume of deformation under hydrostatic pressure.Perforation rate was compared between COMSOL and analytical solution in order to prove the validity of the model.The absorption property and influence of the internal air pressure were analysed based on the interaction model.The results indicate that with increasing of hydrostatic pressure the peak frequency is towards to the high frequency and becomes wider,the more difference is that effect of sound absorption becomes worse;internal air pressure makes the deformation of the cavity decrease and absorption coefficient in low frequency increase.
anechoic coating;sphere cavity;hydrostatic pressure;internal air pressure; absorption property;COMSOL
TB564
:Adoi:10.3969/j.issn.1007-7294.2016.07.014
1007-7294(2016)07-0909-08
2016-03-19
国家自然科学基金(11374369)
张 冲(1987-),男,硕士生,E-mail:chzhang0101@foxmail.com;何世平(1972-),男,副教授,硕士生导师。

