立体几何中的万能公式
2016-05-04 03:38甘肃赵正委
高中数理化 2016年18期
◇ 甘肃 赵正委
(作者单位:甘肃省庆阳长庆中学)
立体几何中的万能公式
◇ 甘肃 赵正委
立体几何是绝大多数学生难啃的“硬骨头”,其空间概念的建立,点、线、面位置关系的判断,让很多学生望而却步.但是,只要在老师的指导下,学会类比、归纳,将知识化成块,将题型分成类,逐块击破,逐类消化,立体几何问题就不再可怕了.
多年来,高考对线线角、线面角、面面角,以及线线距离、线面距离的考查一直是重点,而且涉及到的题目都有一定的难度.下面给出一个重要公式,它可以帮助我们解决几类几何计算问题.

图1


|a|=m,|b|=d,|c|=n,
a与c所成角为γ(θ=γ或θ=π-γ),且
a·b=mdcosα,b·c=-dncosβ,a·c=ancosγ.
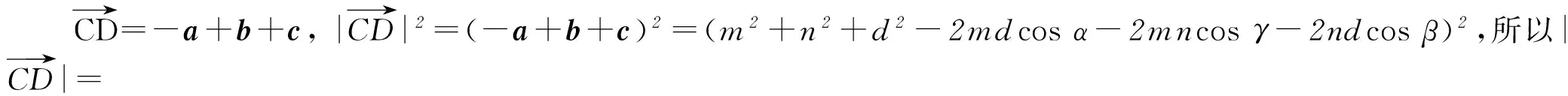
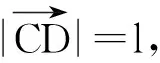

图2
下面是人教版高中数学《选修2-1》中一组形异质同的题目.




此为异面直线上两点间的距离公式.

图3


图4


此为异面直线间距离公式.

图5


此为求二面角的平面角计算公式.

图6




此为求异面直线所成的角(也是求直线与平面所成的角)计算公式.

图7



所以线段BD与平面α所成的角为30°.

此为另一个求异面直线所成角的计算公式.

图8


所以这条线段与这个二面角的棱所成角的大小为45°.
文中开始给出的公式称为“万能”,一点都不为过,它的用途非常广,将空间中线、面之间所成的角及距离问题一网打尽,虽然文章以解决教材中的问题为例来探究,但这只是它广泛用途的很小部分.此文意在抛砖引玉,研究教材,吃透教材,方可驾驭教材,新课改需要彻底改变教与学的方式,但教的背后钻研教材、整合教学内容、确保高效教学更需要坚守.
(作者单位:甘肃省庆阳长庆中学)
猜你喜欢
中学生数理化(高中版.高考数学)(2022年2期)2022-04-26
中学生数理化·高三版(2022年2期)2022-03-30
中国循环杂志(2022年2期)2022-03-07
广东教育·高中(2021年11期)2021-12-01
语数外学习·高中版上旬(2020年8期)2020-09-10
中学生数理化·高三版(2019年8期)2019-12-02
中学数学教学(2019年1期)2019-02-21
中学生数理化(高中版.高二数学)(2018年2期)2018-04-04
西安石油大学学报(自然科学版)(2016年3期)2016-09-05
高中生学习·高二版(2016年9期)2016-05-14

