板块模型题目的突破点

◇ 河南 丁素梅

(作者单位：河南省滑县职业教育中心)



板块模型题目的突破点

◇ 河南 丁素梅

板块模型一直以来都是高考考查的热点，以全国卷为例，2013年全国高考新课标理综II以板块模型为例对牛顿第二定律、匀速直线运动规律、速度-时间图象及摩擦力的概念进行了考查,2015年全国高考新课标理综I又以板块模型为例进行了同样的考查,由此可见板块模型的重要性．此类题目求解的问题一般有以下几种： 1) 动摩擦因数； 2) 块对板的相对位移； 3) 板对地的位移； 4) 块对地的位移．

由于该类问题中大多会涉及摩擦力尤其是静摩擦力.静摩擦力不但方向可变,而且大小也会在一定范围内自我调节,这就给解决问题增加了难度．本文通过2个题目进行研究并作对比，以此总结此类题目的突破点．

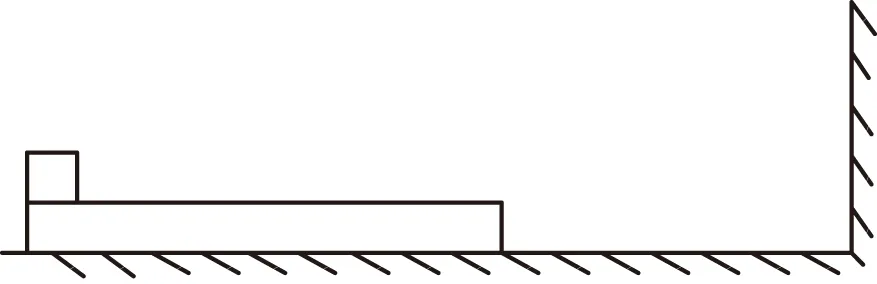
图1

图2

(1) 木板与地面间的动摩擦因数及小物块与木板间的动摩擦因数;

(2) 木板的最小长度;

(3) 木板右端离墙壁的最终距离．

【过程Ⅰ】 板块一起向右做匀减速直线运动,历时t=1 s与墙相碰，由图象可知相碰时木板与物块速度减为vt=4 m·s-1,位移为s0=4.5 m.

由-(15m+m)gμ1=a0(15m+m),解得μ1=0.1.

【过程Ⅱ】 和墙碰撞后物块向右做匀减速直线运动,至速度为0历时1 s,同时板向左做匀减速直线运动,则

由牛顿第二定律有-mgμ2=ma2.故μ2=0.4.

板:由牛顿第二定律有-(15m+m)gμ1-mgμ2=a1·15m，解得a1=-(4/3) m·s-2.

物块速度为0时板的速度

v1=vt+a1t=(8/3) m·s-1.

板:u=v1+a1t2.

可得t2=0.5 s,u=2 m·s-1.

板对地位移大小

所以s=s1+s2=6 m.

图3

(1) 物块与木板间、木板与地面间的动摩擦因数;

(2) 从t=0时刻到物块与木板均停止运动时,物块相对于木板的位移大小．

对块F1=ma1,ma1=μ1mg,所以有μ1=0.2.

对板F2=ma2, -2mgμ2+mgμ1=ma2,所以有μ2=0.3.

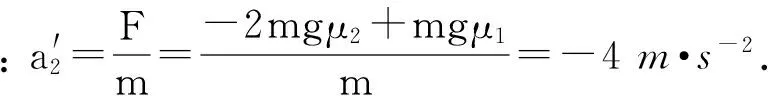
块对地

所以块对板的位移大小Δs=s-s′=1.125m.

寻同找异 例1比例2多了过程Ⅰ和Ⅱ．例1的过程Ⅲ和例2的过程Ⅰ完全相同．在板块具有共同速度以后,2个题目出现了2种情况,例1中板块同步做匀减速直线运动,例2中则是各自做匀减速直线运动．

总结规律 明确板块达到共同速度时各物理量关系是此类题目的突破点: 1) 板块达共同速度以后,摩擦力要发生转变．一种情况是板块间滑动摩擦力转化为静摩擦力;另一种情况是板块间的滑动摩擦力方向发生变化． 2) 板块达到共同速度时恰好对应块不脱离板时板具有的最小长度，也就是块在板上相对于板的最大位移．

(作者单位：河南省滑县职业教育中心)