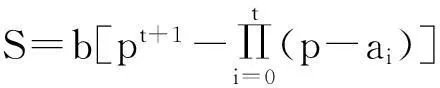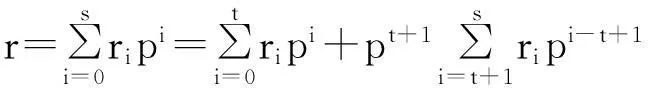杨辉三角的若干性质研究
杨 明 顺
(渭南师范学院 数理学院,陕西 渭南714099)
杨辉三角的若干性质研究
杨 明 顺
(渭南师范学院 数理学院,陕西 渭南714099)
摘要:杨辉三角是二项式系数在三角形中的一种几何排列,通过初等方法及同余运算对杨辉三角中数的奇偶性进行进一步研究,得出杨辉三角中第a行的二项式系数中可被素数p整除的个数,第0行至第a行构成的三角中可被素数p整除的个数,以及每一斜列上的二项式系数中可被素数p整除的个数。
关键词:杨辉三角;素数;二项式系数;同余式
杨辉三角[1]是二项式系数在三角形中的一种几何排列。王先东老师对杨辉三角中数的奇偶性做出了研究,即杨辉三角中的数是否可被素数2整除[2]。本文通过初等方法、同余运算对此问题进行了进一步研究,得出杨辉三角中第a行的二项式系数中可被素数p整除的个数,第0行至第a行构成的三角中可被素数p整除的个数,以及每一斜列上的二项式系数中可被素数p整除的个数。这些结论对于中国剩余定理[3]及相关内容的进一步研究,具有一定的应用价值。
1引理及证明

引理2[5]设p为素数,k,r,t,s∈N,则∀r∈N+,0≤s,r≤p-1,

(1)
证明对r用数学归纳法。注意



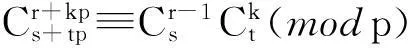
引理3[6]设m是大于1的正整数,(a,m)=1,则aφ(m)≡1(modp)。
证明设r1,r2,…,rφ(m)是模m的简化剩余系,则ar1,ar2,…,arφ(m)也是模m的简化剩余系,于是(ar1)…(arφ(m))≡r1r2…rφ(m)(modm),但(r1,m)=(r2,m)=…=(rφ(m),m)=1,因此(r1r2…rφ(m),m)=1,从而aφ(m)≡1(modm)。
2定理及证明
2.1杨辉三角行的情形

(2)
证明当s≤t时,反复利用引理1,有


(3)

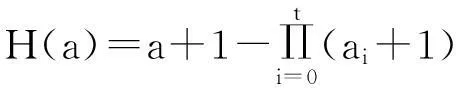





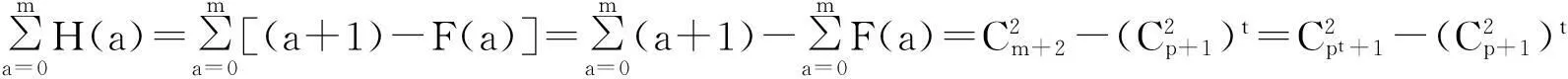
2.2杨辉三角斜列的情形
定理4设p为素数,k,r,t,s∈N,0≤s,r≤p-1,则

(4)
证明用数学归纳法证明。当s=0时,由引理2,有
即(4)式成立。
假定0≤s-1≤p-2时,(4)式对∀r,0≤r≤p-1都成立,那么对s的情形,有
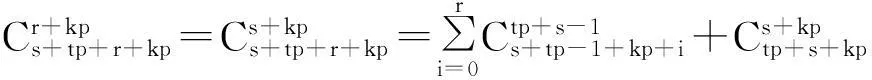
Cr+kps+tp+r+kp=Cs+kps+tp+r+kp=∑ri=0Ctp+s-1s+tp-1+kp+i+Cs+kptp+s+kp
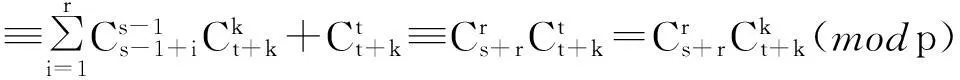
即(4)式对s也成立,由数学归纳法原理知定理4成立。

(5)
证明如果s≥t,反复应用定理4,有

如果s (6) (7) 参考文献: [1] 王先东.杨辉三角中的奇数与偶数[J].数学通报,2009,(5):15-19. [2] 张文鹏.初等数论[M].西安:陕西师范大学出版社,2007. [3] 吴振奎.世界数学名题欣赏——斐波那契数列[M].沈阳:辽宁教育出版社,1987.199-220. [4] 沈虎跃,金国林.杨辉三角中的奇偶分布[J].中学数学月刊,2008,(3):28-29. [5] 潘承洞,潘承彪.简明数论[M].北京:北京大学出版社,1997. [6] 赵继源.初等数论[M].桂林:广西师范大学出版社,2001.9. 【责任编辑牛怀岗】 Some Properties of Yang Hui’s Triangle YANG Ming-shun (School of Mathematics and Physics, Weinan Normal University, Weinan 714099, China) Abstract:Yang Hui’s triangle is a kind of geometric arrangement of binomial coefficients in a triangle. Further research on this issue was studied by elementary methods and congruence arithmetic in this paper, and came to the conclusions that the numbers of binomial coefficients of Yang Hui’s triangle in row a which was divisible by prime number p, the numbers of triangles from line 0 to line a which was divisible by prime number p, and the number of binomial coefficients on each seleme which was divisible by prime number p. Key words:Yang Hui’s triangle; prime number; binomial coefficient; congruence expression 作者简介:杨明顺(1964—),男,陕西渭南人,渭南师范学院数理学院教授,主要从事数论研究。 基金项目:陕西省教育厅科研计划项目:关于F.Smarandache数论问题的计算机辅助研究(2013JK1165);陕西省扶持学科数学学科基金资助项目(14SXZD007);渭南师范学院科研计划项目:数论函数及其在大数据处理方面的应用研究(15YKF005);渭南师范学院教育教学改革研究项目:《复变函数》课程建设的研究与实践(JG201531);渭南师范学院教育科学研究项目:协同创新下师范生职业技能的培养(2015JYKX016) 收稿日期:2015-12-24 中图分类号:O156.4 文献标志码:A 文章编号:1009-5128(2016)04-0009-04 【自然科学基础理论研究】