模糊综合评判方法在边坡稳定性评价中的应用
姜 容,江俊翔,牛红梅,周富华,李庚飞
(广西交通科学研究院,南宁 530007)
模糊综合评判方法在边坡稳定性评价中的应用
姜容,江俊翔,牛红梅,周富华,李庚飞
(广西交通科学研究院,南宁 530007)
摘要:多级模糊综合评价方法在边坡稳定性评判中应用广泛,将层次分析法与模糊综合评价相结合,用层次分析法进行指标权重的确定,再用模糊综合评价与隶属度原则实现边坡稳定性的评价。将该方法应用于省级干线公路重大地质灾害隐患点评估,评估结果与实际调查结果比较吻合,表明模糊综合评判方法有较可靠的预测精度。
关键词:多级模糊综合评价;层次分析法;边坡稳定性评判
干线公路边坡失稳所造成的地质灾害因其普遍与突发性给人类的生活带来不便,造成各种交通行为损失,为了及时精准地判断边坡的稳定性,以便合理预防,从定量到定性对干线公路边坡稳定性的研究进行方向性转变。地质环境上由于干线公路边坡具有多样性、变异性和复杂性,导致各评价因子的不确定性。考虑到这种不确定性所带来模型上的模糊性,选择模糊综合评价法对边坡稳定性进行评判。
广西位于我国西南部,以山地为主,地质环境条件复杂,改革开放特别是西部大开发以来,广西干线公路建设取得了飞速进展,伴随而来的是各种干线公路地质灾害频发,其中以边坡隐患占大多数,应用模糊数学综合评价法对广西公路干线边坡隐患点进行稳定性评判,为边坡治理与监测提供指导建议。
1多级模糊综合评价方法
1.1模糊综合评价原理
如果论域U中的任意元素u对集合A满足:0≤μA(u)≤1,则称μA(u)为A的隶属函数,且μA(u)确定了论域U上的一个模糊子集A。[1]
有因素集和评价集分别如下:
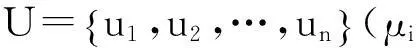
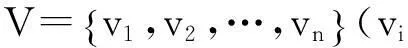
通过评价规则对U中的元素μi作出评价f(μi),评价f是U-V的模糊映射,推导出从U到V的单因素评价矩阵R[2]:
R=(rij)n×m(0≤rij≤1)。
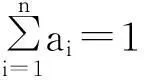
从U到V可由权向量ai唯一确定一个模糊变换B:
B=A·R,
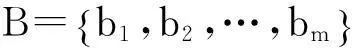
其中:bj(j=1,2,…,m)称为综合评价结果向量,反映出Vj与模糊集B的隶属度。
1.2多级模糊评价方法
模糊综合评价方法[2]步骤如下:
(1)通过对边坡地质灾害危险源因子的辨识,建立了边坡地质灾害危险源的因子集U,进一步建立危险源因子分级标准,考虑目前国内外的分级方法中的分级档数建立评价集V。结合广西干线公路地质环境,将边坡地质灾害危险源分为稳定、较稳定、基本稳定、较不稳定、不稳定5级[3],分别用数字1~5表示。并由评价等级得出评价集V:
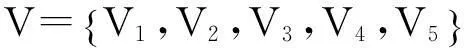
(2)对已经辨识的危险源因子采用模糊数学方法建立隶属函数,并对隶属函数根据实际情况进行选取。通过隶属函数求出评价指标相对应的隶属度,可得一级模糊关系矩阵R:

(3)通过层次分析法得到了边坡地质灾害危险源的一级权重A1和二级权重A2。[4]
(4)模糊综合评价。
一级综合评价可以通过下式运算得出:
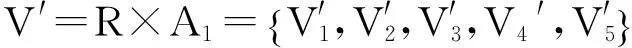
其中:R是一级模糊关系矩阵,A1是基础指标权重矩阵。
二级综合评价可以通过下式运算得出:
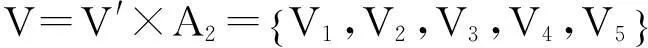
其中: V′是二级评价的模糊关系矩阵,A2是二级权重矩阵,Vi为评价集V中因子i的隶属度。
2隶属函数的确立
对边坡地质灾害进行评价因子隶属函数的建立一般分为两类:离散型(定性因子)和连续型(定量因子)。[6]
建立边坡隶属函数如下:
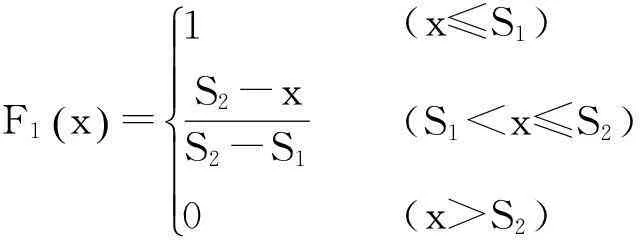
F1x()=1S2-xS2-S10ìîíïïïïï (x≤S1)(S1
,

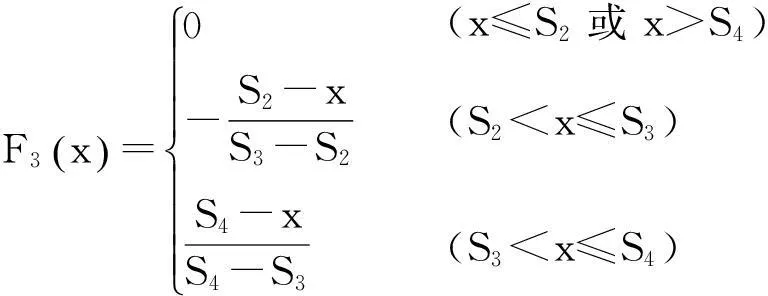
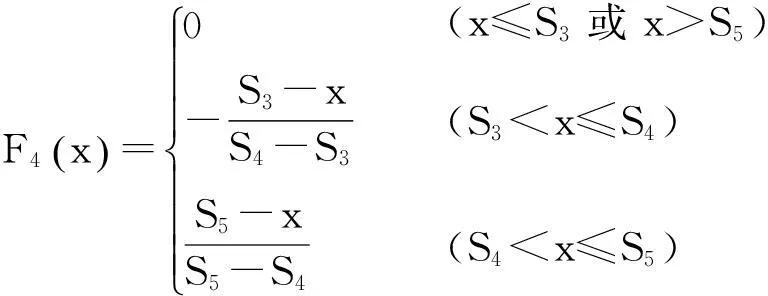
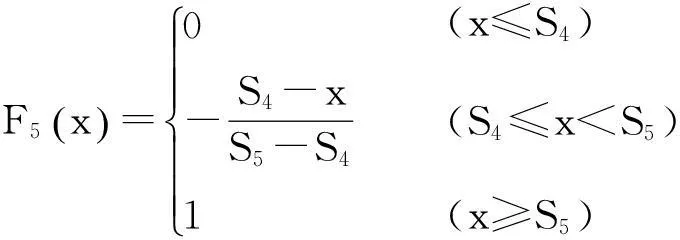
其中:x为待测边坡相关因子的实测值,S1~S5分别为各评价因子在稳定、较稳定、基本稳定、较不稳定、不稳定这5种稳定状态下对边坡影响的标准值。
对离散型的评价因子,借助层次分析法中两两比较构造各因子等级对边坡等级的判断矩阵,可获得隶属度。
3指标权重的确定
评价指标权重对评价结果的影响重大,在确定评价指标权重时,可根据其重要性和影响程度客观确定[3]。
指标权重确定的步骤如下:
(1)建立层次结构模型
将一个复杂的系统或者目标分解成小的组成部分或因素,每个因素又可以分解成其他子因素,各个因素之间的性质和相互之间关系可以构成递阶层次结构,这种层次结构模型自上而下通常包括目标层、准则层、指标层等。
(2)构造判断矩阵
通过对于已经建立好的层次结构模型来构造判断矩阵(见表1)。
从第二层开始,按照表1所示的规则对因素层和子因素层间各元素的相对重要性给出评估并且赋值,构造判断矩阵。[7]

表1 判断矩阵构造过程
(3) 计算层次单排序
层次单排序即本层各个元素对上一层与其相关元素的重要程度(即权重值)的次序,本次研究通过计算判断矩阵的最大特征值和特征向量来求得。[8]
实现的基本步骤如下:
第一步,建立判断矩阵A:
对矩阵A的列向量进行归一化,得
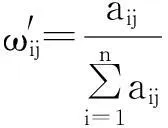
第二步,对ωij′按行求和,得
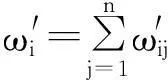
第三步,将ωi′归一化,得
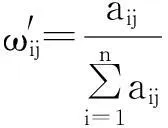
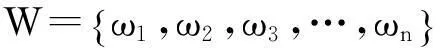
第五步,矩阵一致性检验:
一致性检验的目的是保证计算结果基本合理,计算公式如下:[9]
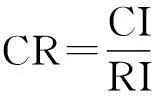
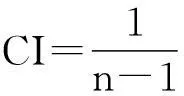
当CR<0.1时,检验判断矩阵满足一致性要求,否则需调整矩阵。CR愈小,矩阵一致性愈好,当CR=0.1时,矩阵完全一致。[10]

表2 随机性指标的取值
(4)计算层次总排序
层次总排序是指同一层次所有因素对于上一层的相对重要性的排序权值。具体步骤如下(见表3):
第一步,计算A层总排序,得其权值分别为a1,a2,…,am;
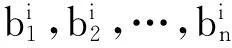
(5)层次一致性检验
层次一致性检验由下式进行:
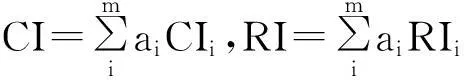
其中:CIi代表Ai对应的B层次中判断矩阵的一致性指标;RIi代表Ai对应的B层次中判断矩阵的随机一致性指标。[11]
计算层次总排序一致性比例CR(CR<0.1),结果满意一致性要求:
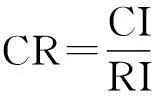
。
4应用实例
对广西干线公路沿线边坡选取评价因子如图1所示。

图1 广西公路边坡层次结构模型图
在将评价因子分类和编号后,建立模糊综合评价因子集如下:
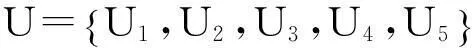
将5个评价因子用二级因子表示如下:
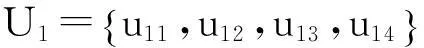
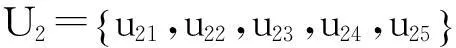
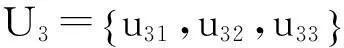
降雨U4={U41}={降雨强度};
地震U5={U51}={地震烈度}。
依据层次分析理论的“1~9标度法”(见表1),分别对各层中的因子相对上一层次目标的重要性进行两两比较,构造危险源因子重要度比较矩阵,即判断矩阵如表4—表7所示。
(1)构造判断矩阵
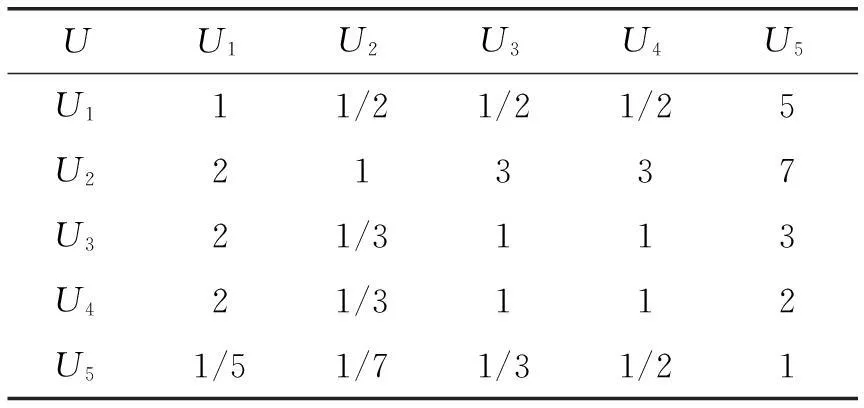
表4 边坡地质灾害判断矩阵U
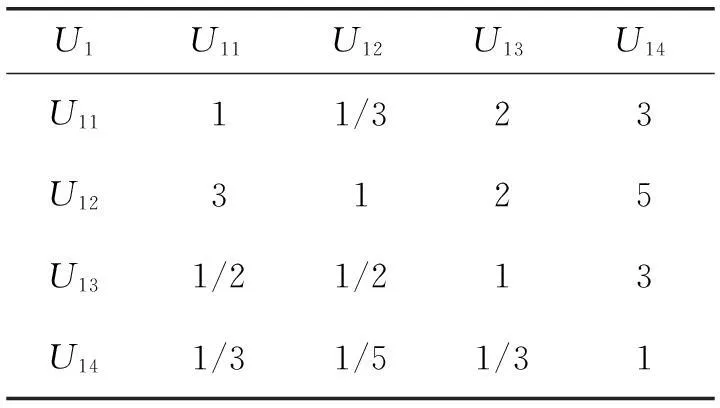
U1U11U12U13U14U1111/323U123125U131/21/213U141/31/51/31
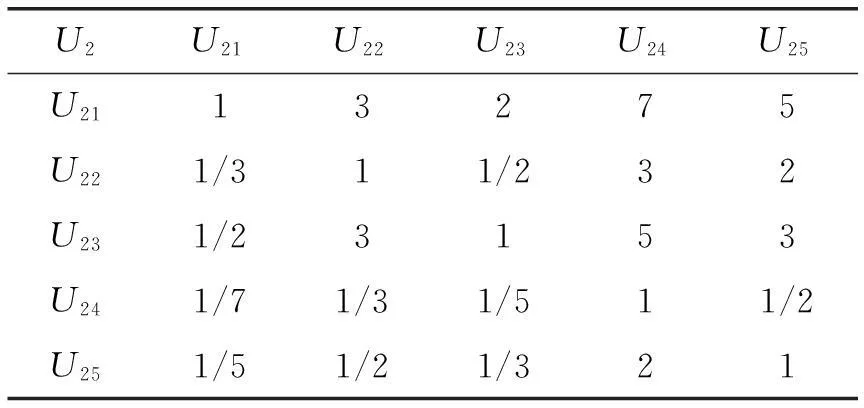
表6 边坡地质灾害判断矩阵U2
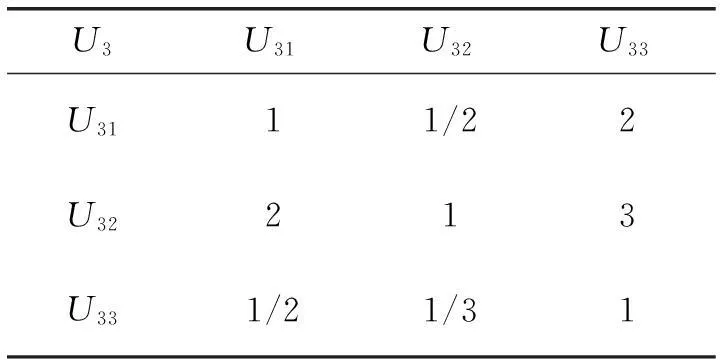
表7 边坡地质灾害判断矩阵U3
(2)计算最大特征根和特征向量(即权重)
以矩阵U为例,最大特征值λmax=5.28,归一化特征向量为(0.15,0.43,0.19,0.17,0.06)。
(3)一致性检验
判断矩阵阶数m=5,查表2得到相应的一致性指标RI=1.12,CI、CR按下式计算:
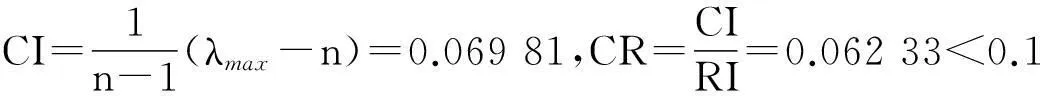
故判断矩阵满足一致性检验,权重分配合理。
边坡地质灾害危险源评价因子权重分配见表8。

表8 边坡地质灾害危险源评价因子权重分配表
对广西105处重大地质灾害危险源中未进行治理的77处进行稳定性评判,评价结果见表9。

表9 地质灾害危险源稳定性评判结论表

危险源编号危险等级G209H22S307H12S334H13X638H52S309H92S309H162S309H172G321H43G321H55G321H65G321H74G321H85G321H95G321H134G321H153G321H193SL-1762BY-1672LG-H0113LG-B0172LG-B0191LG-B0211LG-B0234QZ-B0284QZ-B0322QZ-H0341

危险源编号危险等级QZ-B0444QZ-B0454QZ-B0462XA-H073XA-H093XA-H0244ZY-H0185ZY-H0205GY-B0125GY-B0143GY-B0193HC-1493HC-1754HC-1774CZ1654G65LX093G324-084G324-092S108-012S212-164S323-154S323-172PQ-072PQ-091PQ-225
5结论
(1)根据评价结果与现状稳定性对比,评价结果与现状稳定基本无差异,发现除融水H06、ZY-H020及G324-08稳定性有出入外,其他都基本吻合。
(2)从以上分析不难看出,利用多级模糊综合评价方法来评价边坡稳定性是可取的,可以用来评价边坡的稳定性。
(3)在进行稳定性评判之后,要进行危险性评价,需要考虑是否治理、危害程度等因素,要做更深入细致的分析研究工作。
参考文献:
[1] 王学武,石豫川,黄润秋,等.多级模糊综合评价方法在泥石流评价中的应用[J].灾害学,2004,19(2):1-6.
[2] 姜容.滑坡防治菱形格构锚固体系数值模拟及安全检测方案研究[D].西安:长安大学硕士学位论文,2013.
[3] 孙佳伟.略阳县地质灾害风险评价研究[D].西安:长安大学硕士学位论文,2012.
[4] 王连芬,许树柏.层次分析法引论[M].北京:中国人民大学出版社,1990.
[5] 刘震.层次分析模型AHM及其应用[J].河北建筑科技学院学报,2003,20(3):78-81.
[6] 张业成,张春山,张梁.中国地质灾害系统层次分析与综合灾度计算[J].中国地质科学院院报,1993,(27-28):139-154.
[7] 徐梅.第四方物流中3PLs合作伙伴的选择与管理[D].湘潭:湘潭大学硕士学位论文,2007.
[8] 王国良.层次分析法在地质灾害危险性评估中的应用[J].西部探矿工程,2006,125(9):286-288.
[9] 骆正清,杨善林.层次分析法中判断矩阵构造的新方法[J].电子科技大学学报,1999,28(5):557-561.
[10] 陈善雄,徐海滨,秦尚林,等.层次分析法在斜坡失稳灾害预测评估中的应用[J].土工基础,2005,19(4):8-13.
[11] 门玉明,王勇智,郝建斌,等.地质灾害治理工程设计[M].北京:冶金工业出版社,2011.
【责任编辑牛怀岗】
Application of Multi-Layer Fuzzy Comprehensive Evaluation Method in Evaluation of Slope Stability
JIANG Rong, JIANG Jun-xiang, NIU Hong-mei, ZHOU Fu-hua, LI Geng-fei
(Guangxi Transportation Research Institute, Nanning 530007, China)
Abstract:The paper introduced the principle of multi-layer fuzzy comprehensive evaluation and application of multi-layer fuzzy comprehensive evaluation to the evaluation of slope stability that was based on the principle of this method. This method combined analytic hierarchy process with the multi-layer fuzzy comprehensive assessment method, and the paper used the analytic hierarchy process (AHP) to conform the weighted coefficient. Then the slope stability were evaluated based on multi-layer fuzzy comprehensive evaluation. The method was used to evaluate the stability of trunk highway in Guangxi. The result of the evaluation was satisfied when it was compared with the result of the field investigation. The method of multi-layer fuzzy comprehensive evaluation has better control precision and adaptability.
Key words:multi-layer fuzzy comprehensive evaluation; AHP; evaluation of slope stability
作者简介:姜容(1987—),女,湖南常德人,广西交通科学研究院工程师,工学硕士,主要从事地质灾害危险性评估研究;李庚飞(1978—),女,内蒙古通辽人,广西交通科学研究院副教授,工学博士,主要从事环境污染与生态修复研究。
基金项目:广西壮族自治区交通运输厅科技项目:广西公路地质灾害智能监测预警系统开发(桂交科教发[2013]100号);广西壮族自治区交通运输厅科技项目:广西干线公路地质灾害辨识、危险性评价与防治对策研究(桂交科教发[2012]26号)
收稿日期:2015-08-29
中图分类号:U416.1+4
文献标志码:A
文章编号:1009-5128(2016)04-0036-08

