巧变课本习题 点燃思维火花

☉浙江省黄岩实验中学　章文菊



巧变课本习题点燃思维火花

☉浙江省黄岩实验中学章文菊

运用习题举一反三，是习题课中常用的教学手段.众所周知，一堂数学习题课的成功，关键在于对习题的精心选择.若所选的习题蕴含一定的针对性、示范性、趣味性、综合性等特点，不仅可以帮助学生走出知识误区，更能激发学习兴趣，拓宽解题思路，提升思维能力.教材中的习题是专家从大量的“原材料”中经过仔细斟酌、筛选、检验、考证后才形成的“产品”，具有较强的典型性，有极高的研究价值.只要教者注意对习题进行创造性的设计，包括对习题的选择、挖掘、引申、改编，就一定能取得理想的教学效果.在此，笔者以人教版教材“四边形”一章为例，谈谈几年来在习题课教学中的一些探索，作为抛砖引玉吧！

一、以课本练习为基础题型，不断增加问题的综合性，培养学生的观察能力

原题1（八下第44页练习2）如图1，平行四边形ABCD的对角线AC、BD相交于点O，EF过点O与AB、CD分别相交于点E、F.求证OE=OF.

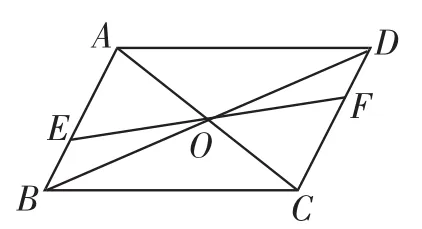
图1

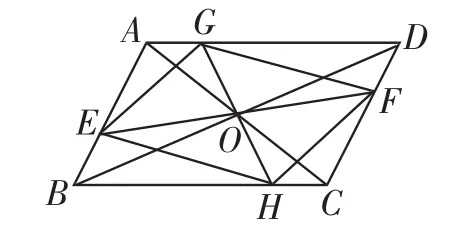
图2

解决此题的关键是平行四边形性质定理的应用，并通过△AOE≌△COF来达到目的.但在此题的条件下，全等三角形不只是以上一对.因此，我们可以此题为基础题型，进行如下的变式、复合：

变题1：用此题的条件及图形，找出图中有几对全等三角形.

这就要求学生必须通过仔细观察，利用全等三角形的判定，才能准确地完成此题.

变题2：增加条件：GH过点O与AD、BC分别相交于点G、H（图2），求证四边形EHFG是平行四边形.

这样，此题就可转化为平行四边形判定定理的应用，但图形明显比以前复杂.只要观察出两图形的关系，问题就可迎刃而解.

变题3：再增加条件：若GH⊥EF，求证∠EGH= ∠FGH.

至此，本题就变成一道寓平行四边形的性质和判定、菱形的性质和判定等诸多知识的综合题.由于菱形是特殊的平行四边形，增加条件GH⊥EF后，就可利用菱形与平行四边形对角线之间的关系，得到四边形EHFG是菱形，再由菱形的性质可得∠EGH=∠FGH.

二、以课本例题为参照题型，不断改变例题中的部分条件，使学生在解题中自觉做到举一反三

原题2（八下第46页例3）如图3，平行四边形ABCD的对角线AC、BD交于点O，E、F是AC上的两点，并且AE= CF，求证四边形BFDE是平行四边形.

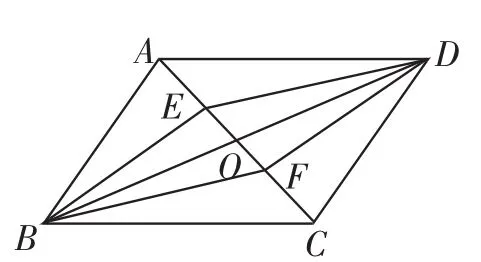
图3

此题可从对角线的角度来证明，也可用平行四边形的边、角关系，由三角形全等知识来证明.

变题1：若把此题中的条件“AE=CF”改成“BE平分∠ABC交AC于点E，DF平分∠ADC交AC于点F”，那么，四边形BFDE仍是平行四边形吗？

利用平行四边形对角相等的性质，是解决此题的关键.

变题2：把此题中的条件“AE=CF”改成“BE⊥AC于点E，DF⊥AC于点F”，那么，四边形BFDE还是平行四边形吗？

此题就要利用垂直的定义和三角形全等的知识，再结合平行四边形的性质和判定来解决.

由原有例题引发出的变式题的讲解和练习，既可让学生熟练地掌握平行四边形的各种判定和性质，又能使学生在解题中进行举一反三，触类旁通.

三、以课本复习题为背景题型，改变课本习题，进行一题多解，提高学生的解题能力

原题3（八下第69页复习题第14题）如图4，四边形ABCD是正方形，E是边BC的中点，∠EAF=90°，且EF交正方形外角的平分线CF于点F，求证AE=EF.

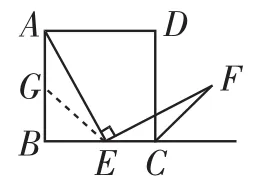
图4

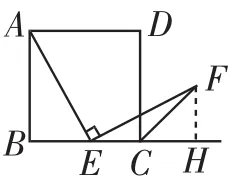
图5

图6

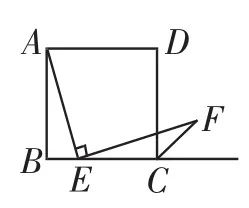
图7

方法1：如图4，取AB的中点G，连接GE，则AG=BG= BE=EC，进而得出∠BGE=45°，所以∠AGE=∠ECF= 135°.又不难证明∠BAE=∠FEC，于是△AGE≌△ECF，从而得出结论.

若作为一节九年级的习题课，还可以从以下两种方法去引导：

方法2：如图5，过点F作FH⊥BC于点H，由此可以证明△ABE∽△EHF，进而可得，由比例性质可得.又△FCH是等腰直角三角形，故有EH-FH=EH-CH=CE，同时易证AB-BE=BC-BE=CE，从而有，所以BE=FH，就可以证得△ABE≌△EHF，得出结论.

方法3：如图6，连接AF、AC，因为∠ACD=45°，∠DCF=45°，可以证得∠ACF=90°，从而有点A、E、C、F四点在以AF为直径的圆上，由同弧所对的圆周角相等，知∠AFE=∠ACB=45°，结论得证.

当然，本题还可以变式为一般情形，即E是BC边上的任意一点，如图7所示，也可以采用以上三种方法进行解答.

上述几种方法既体现了几何题一题多解的特点，同时又进行了全面复习，也是对所学知识的一次整合.

四、以课本习题为基本题型，进行一题多变，提升学生的发散性思维

原题4（八下第68页复习题第8题）如图8，四边形ABCD是一个正方形花园，E、F是它的两个门，且DE=CF，要修建两条路BE和AF，这两条路等长吗？它们有什么位置关系？为什么？

分析：本题思路特别简单，利用三角形全等去证明两条线段相等及位置关系，为了进一步提升学生的思维，先从点E、F的位置上进行改编：

变题1：如图9，在正方形ABCD中，已知点E、F分别在边AD、DC的延长线上，且DE=CF，连接BE、AF相交于点P.

（1）试说明：AF=BE；

（2）求∠BPF的度数.

再把这两条直线的位置加以改变，同时添加垂直的条件，证明它们相等.

变题2：如图10，在正方形ABCD中，M、N、P、Q分别是边AB、BC、CD、DA上的点，且MP⊥NQ，MP与NQ是否相等？并说明理由.

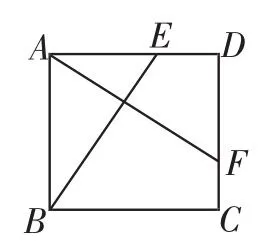
图8

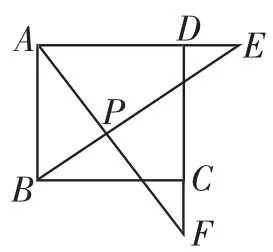
图9

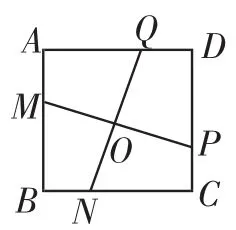
图10

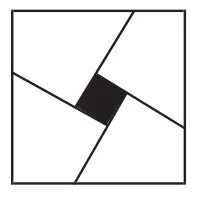
图11

继续由直线位置改变为四个点的位置，并转化成面积问题.

变题3：如图10，在正方形ABCD中，M、N、P、Q分别为边AB、BC、CD、DA上的点，AM=BN=CP=DQ，连接MP，NQ，交点为O.

（1）求证：MP⊥NQ，MP=NQ；

（2）将正方形ABCD沿线段MP、NQ剪开，再把得到的四个四边形按图11所示的方式拼接成一个四边形，若正方形ABCD的边长为3cm，MA=NB=PC=QD=1cm，则图11中阴影部分的面积为_____cm2.

最后借助垂直条件，将其改编成一道综合性强的几何题.

变题4：如图12，正方形ABCD中，E、F分别为边AD、DC上的点，且AE=FC，过点F作FH⊥BE，交AB于点G，连接BF，DH，求证：

（1）∠BGF=∠CFB；

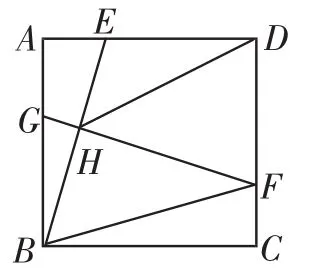
图12

解题思路：（1）由BE⊥GF可知BE=GF，又由AE=CF可证BE=BF，所以GF=BF，则∠BGF=∠ABF.又由AB∥DC得∠ABF=∠CFB，从而得出结论.

（2）由于出现了线段和，可以延长HE到点M，使EM= HF，连接DM，证△DEQ≌△DFH，从而得到△QDH为等腰直角三角形，结论得证.