挖掘网格图形几何特性，贯通三角函数求解路径——对一道中考试题的讲评与反思

☉浙江省宁波东海实验学校　陈明儒



挖掘网格图形几何特性，贯通三角函数求解路径——对一道中考试题的讲评与反思

☉浙江省宁波东海实验学校陈明儒

一、试题展示

题目如图1，在边长相同的小正方形组成的网格中，点A、B、C、D都在这些小正方形的顶点上，AB、CD相交于点P，则tan∠APD的值是________.

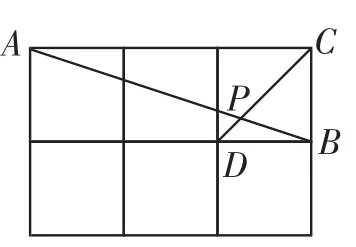
图1

这个问题是新近九年级三角函数单元测试的一个填空题，序号是第16题，来源于2012年泰州市中考数学试题第18题.简明的问题，简洁的网格图形，融几何、三角函数于一体，深受老师们的喜爱.但是考试结果出人意外，得分率很低.考后，笔者对这个问题进行了重点讲评，课堂上学生思维活跃，发言踊跃，解法之多，出乎笔者预期，课后师生收获多多.现将讲评过程呈现出来，与大家分享.

二、讲评片段实录

1.正面突破，颇费周折

师：大家猜猜这次考试得分最低的是哪一题？

众生：第16题吧！

师：是的，现在，我们一起解决这个难点问题.请做对的学生讲一讲你们的思路.

生1：（解法1）如图2，连接AD，作DH⊥AP于点H.设图中的小正方形的边长为1，因为S△ABD=BD·BC=AB·DH，所以DH=.由于BD∥ AC，则△BDP∽△ACP，所以，所以DP=.在Rt△DPH，PH=，所以tan∠APD==2.

图2

师：好样的！将所求的角放到一个直角三角形中，再利用三角函数定义求解.如果这样的直角三角形没有，就想方设法正面构造直角三角形.还有其他的构造法吗？

生2：（解法2）如图3，过点A 作CD延长线的垂线，垂足为G.因为∠ACG=45°，所以∠CAG=45°，于是AG=CG，且线段AG经过格点.由解法1，得DP=CD，DG=CD，所以PG=CG=AG.所以tan∠APD==2.

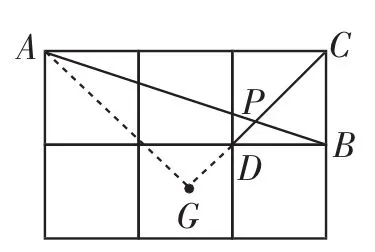
图3

师：不错！同样是构造直角三角形，显然计算量小了，令人眼前一亮.还有吗？

生3：（解法3）如图4，连接AE、BE、ED，作EH⊥AP于点H，则△ABE是等腰直角三角形，因此EH=AB= AH=BH.又因为BP=AB，所以PH=AH.同样求得tan∠APD==2.

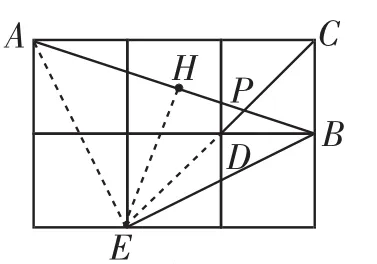
图4

师：你考试时就是这样做的？

生3：不是.经过刚才两位同学的启发才想到的.

师：好啊！倾听别人的想法，提出自己的观点，这是一种高效的学习方法.生4，说说你的正确理由.

生4：我是猜的，考试的时候时间来不及了（大家都笑了）.

师：你真走运.

2.等价转换，柳暗花明

师：其他同学还有不同的思路吗？

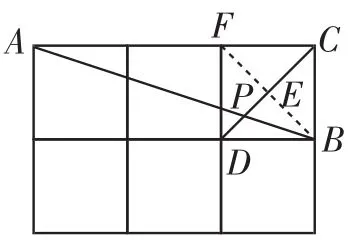
图5

生5：（解法4）如图5，取格点F，连接BF交CD于点E.则CD⊥BF.由于BD∥AC，所以△BDP∽△ACP，所以.又因为四边形DBCF为正方形，所以DE=CE=BE.因此，BE=2DP=PE.在Rt△BEP中，tan∠BPC==2.于是tan∠APD=tan∠BPC==2.

师：行啊！解法4给我们打开了另一种思路，即当所求的角不在直角三角形或三角形中时，将所求角转化到相对容易求解的等角上，这种方法不同于前面三种解法，还有吗？

生6：我也是求先求∠BPC的正切，只是有点繁，考试后才想出来的.

师：没关系，说来让大家听听！

生6：（解法5）如图6，画CH⊥AB 于H.因为∠ACB=90°，依据射影定理，BC2=BH·AB，AC2=AH·AB，于是可得又因为△BDP∽△ACP，所以.令AB=20k，则AP=15k，BP=5k，BH=2k，所以PH= 3k.根据射影定理，CH2=BH·AH=2k·18k=36k2，可得CH= 6k.所以tan∠APD=tan∠HPC=

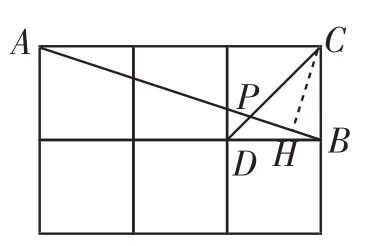
图6

师：虽然计算量大点，但是能想到用射影定理，相当了不起.大家继续.

生7：（解法6）如图7，取格点E，连接BE，AE，则四边形DEBC为平行四边形，于是CD∥BE，则∠APD= ∠ABE.又因为∠AED=∠BED=45°，所以∠AEB =90°.在Rt△AEB中，tan∠ABE===2.因此tan∠APD=tan∠BPE==2.师：大家评价一下生7的解法.众生：方法6最简单.

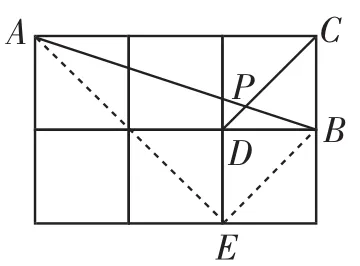
图7

师：这种角的转换确实巧妙，让原来困顿的问题一下柳暗花明.那你是如何想到的？

生7：其实我考试时也没想到，是刚才受解法2中的图3启发，将线段AG延长，于是有了这种解法.

师：解法6告诉我们，只要将∠APD转化到两直角边之比为2的直角三角形中即可.因此，有时不要忙于画垂线，构造直角三角形，而是要仔细琢磨网格图中的关键点和重要线段，画出现成的直角，通过等角转换，在新的直角三角形中解决问题.这是解决此类网格问题的关键，它考验我们的几何直观与空间想象，当然离不开推理与计算.

图8

生8：（解法7）如图8，取格点F，延长CD、AE，两线交于点E.设AE= 3，则ED = 2由△APE∽△BPC，得=3，所以EP=，所以.又因为∠AED=∠PEA，所以△APE∽△BPC，于是∠APD= ∠FAD.

师：看来大家的思路已经打开了.

生9：（解法8）如图9，取格点E、G，延长CD、AG，两线交于点F，连接EB.由于∠AEF=∠AEG+ ∠GEF =∠APD +EAB，∠GEF = ∠EBF =∠EAB =45°，所以∠AEG=∠APD.所以tan∠APD= tan∠AEG==2.

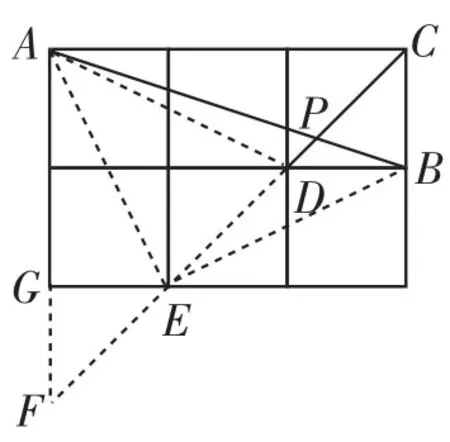
图9

师：解法4至解法8，本质上是一种“以退为进”的解题策略，即将所求角转移到一个容易求得三角函数的等角中，再求等角的三角函数.大家的思维变得越来越开阔，真棒！再回顾前面8种解法，相同之处都要添设辅助线，构造直角三角形.那么，不添辅助线能解决这个问题吗？

3.居高临下，茅塞顿开

生10：（解法9）如图1，设BC=1，由于△BDP∽△ACP，则

因为S△BCP=CP·BC·sin∠BCP=CP·BP·sin∠BPC，所以sin∠BPC=

师：用面积法，再借助同角三角函数关系求解，这种方法其实已经是高中生的解题手法，因为高中的三角函数中的角不局限于锐角，因此不一定在直角三角形求三角函数.太厉害了，这个面积公式老师以前上课是讲到过，但这里能用上来，太了不起！

生11：（解法10）如图1，设BC=1，由于△BDP∽△ACP，则