疑、思、悟：导学案应循三条原则——以人教版“14.2.1平方差公式”为例

☉天津市静海区沿庄镇中学　刘家良



疑、思、悟：导学案应循三条原则——以人教版“14.2.1平方差公式”为例

☉天津市静海区沿庄镇中学刘家良

导学案是引导学生自主求知的方案.而在日常教学中，学案的使用大多成为了一张学生解题的试卷，或者为教材的“分段”翻版，有听课时用一用，没有听课的就扔到了一边，这种流于形式上的导学案现象，造成教与学的脱节，违背了导学案设计的初衷.导学案不单单是突出重点、突破难点的一个知识流程图，更要承载学生对所学知识产生浓厚好奇心的效能，产生一种揭开神秘“面纱”的驱动力，通过引导学生通过算一算、议一议、推一推等环节经历知识的探究和形成过程，从中有感、有悟，在反思中升华其中蕴含的思想、方法，力求收到授人以渔的效果.现以人教版“14.2.1平方差公式”的学案为例，旨在与同仁交流学案设计应循的一些原则，注意理清两种关系.

一、学案展示

（一）学习目标

（1）经历平方差公式的形成过程，知道平方差公式是由两个特殊的多项式相乘为条件的；

（2）从平方差公式的形成过程中，感受从一般到特殊再到一般的辩证思想，养成主动观察、善于发现的求知品质；

（3）掌握平方差公式的结构特征并能应用公式计算、化简.

（二）学习重难点

学习重点：平方差公式的结构特征及其应用；

学习难点：用平方差公式的结构特征判断所给的式子能否使用公式计算、化简.

（三）学习过程

1.情境引入，趣味感知

小强带小刚去超市购买了单价为4.9元/千克的瓜子5.1千克，售货员刚拿起计算器，小强就说出应付24.99元，结果恰与售货员算出的结果相吻合，小刚惊讶地说：“你怎么算得这么快？”小强自豪地说：“我是用了数学上的一个公式.”你知道小强用的是一个什么样的公式吗？

设计意图：通过这一情境旨在激起学生的好奇心和求知欲，营造出一个探究的氛围.

2.自主探究，潜能开发

算一算：（1）（a+2）（a-2）=_______；（2）（3+q）（3-q）= ______；（3）（2x+1）（2x-1）=_______.

设计意图：提供探究素材，复习多项式乘法法则，因为平方差公式植根于多项式乘法运算之中.同时旧中出新，为下一环节埋下伏笔.

议一议：观察3个题中左边的算式和右边的结果，你从中发现了什么规律？并用字母表示这种规律.请你再找几组类似的算式加以验证.

设计意图：观察是思维的先导，通过观察让学生在习以为常或熟知的东西中找出不寻常的东西，从中让学生感知、发现和猜想.

推一推：（a+b）（a-b）=a2-b2.

证明：（a+b）（a-b）=a2-ab+ab-b2=a2-b2.

设计意图：理解平方差公式与多项式乘法法则之间的联系，从公式的形成中感受从一般到特殊再到一般的辩证思想.

归一归：平方差公式：__________；用文字表述为：________.

设计意图：培养学生概括、归纳及语言间转换表达的能力.

验一验：你能根据图1中图形的面积验证平方差公式的正确性吗？

设计意图：从式子（a+b）（a-b）联想到一个长为（a+ b）、宽为（a-b）的长方形，并进一步认识到这个长方形是将一个边长为a的正方形相邻两边分别加b和减b获得的，从中感受“形”给“数或式”研究带来的直观性，同时验证平方差公式的正确性.认识一个数学对象描述的三种语言.

3.检测新知，挑战技能

选一选：下面各式的计算中正确的是（）.

A.（x+2）（x-2）=x2-2

B.（3x+2）（3x-2）=3x2-4

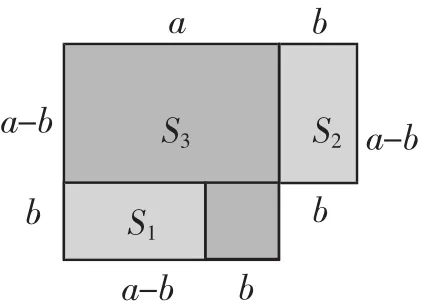
图1

C.（-3a-2）（3a-2）=9a2-4

D.（-x+2y）（-x-2y）=x2-4y2

（2）（2x+3y）（-2x+3y）=_______；

（3）103×97=_______.

设计意图：通过选一选、填一填等练习理清平方差公式的结构特征，知道公式中的字母a、b既可以表示数，又可表示单项式、多项式等式子，从而拓宽公式的应用范围.

做一做：（1）（a+3）（a-3）（a2+9）=______；

（2）（0.2m-3n）（3n+0.2m）=_________.

设计意图：通过递进和变换性的训练，培养学生的应变能力，熟练掌握平方差公式.

问题解决：能用你学到的平方差公式知识帮助小刚速算一下应付的钱数吗？

设计意图：感受平方差公式的应用价值，激起应用公式解决问题的积极性.

4.反思拓展

（1）平方差公式与多项式的乘法法则之间有什么联系？通过平方差公式的学习，对你今后的解题有什么启发？

（2）在两个多项式相乘的运算中你还有什么新的发现吗？

（3）计算：（2+1）（22+1）（24+1）（28+1）.

设计意图：感受知识之间的内在联系，感受观察在发现中的不可或缺性，养成主动观察、善于思考和勇于发现的求知品质.

5.达标测试

（1）对号入座：

（a+b）（a-b）　a　 b　 a2-b2最后结果（2x+3y）（2x-3y）（-2x+3y）（2x+3y）（-2x-3y）（2x-3y）

（2）填一填：

①（m+n）·（______）=n2-m2；

②（______）·（______）=9a2-4b2；

③（5-a）·（a+5）=_______；

④若（a+b+c）（a+b-c）=A2-B2，则A=______，B= ______.

设计意图：通过对号入座、填一填等练习考查学生对平方差公式在不同情境下的掌握程度，兼顾到逆向和整体性意识的考查.

（3）算一算：

①（3x+4）（3x-4）-（x+3）（x-2）=________；

②20102-2011×2009=________.

设计意图：通过练习考查学生对平方差公式结构特征的把握和应用的灵活性，检测学生的综合力和严谨性.

6.附参考答案

供学生检查自己预习的效果，做出信息反馈，为课堂上与同伴、老师交流能挤出更多的时间.同时信息反馈也为教师以学定教提供了第一手材料.

二、设计导学案应循三条原则，理清两种关系

1.疑中生趣性原则

学生一接触到学案中“学习过程”的第一环节（情境引入，趣味感知）就会被所学知识牢牢吸引，会产生一种急于探个究竟的念头.这就需要教师对教材知识有一个重新加工、塑造的过程，而其中情境创设的过程就彰显出教师劳动的创造性.上述案例就采用了“倒叙”的方法，由应用平方差公式获取的果实放到了“开篇”，激起了学生思维的涟漪.

2.渐进导思性原则

数学中的每个知识点都是前后紧密联系衔接的，导学案要将新、旧知识点有机结合起来，旧中引新，在已有知识的复习巩固中悄然地过渡到所学知识之中，其间的观察、猜想、发现、实验、验证、概括、归纳是探究发现的重要途径，这是导学案功能的核心所在.

3.悟中升华性原则

思、悟二者间是相互联系、相互渗透和相互作用的.感悟本节课中所学的知识，从中寻找出探究的主线，初步形成辩证的思维和思想，这是导学案的精髓所在.

鉴于日常导学案使用中教与学间脱节的现象，要理清两种关系：

（1）课本与学案的关系.

有了学案但不能将课本扔到一边去.对学生在学案中遇到的问题，教师要发挥学案的导读作用，让学生揣着问题拜读教材.学案中试题的来源，可将教材中的题通过分解（深入浅出）或变式（让学生蹦一蹦能解决）再移到学案中.学案源于教材，又要别于教材，学案不等同于将教材简单“分段”.

（2）解题与探究的关系.

学数学离不开计算和推理.所以导学案中必然离不开解题内容的训练，在新知萌芽的初期，设计的题目就要围绕新知的产生来设计，这样的铺垫既能巩固旧知，又能诞生新知.在新知应用的初期，要循序渐进、有梯度地组题，融入新学的概念、法则、定理的内容，在梯度性的练习和探究中揭示这些知识的内涵与外延，同时警示学生易错、易混的东西.

学案需要以学生现有的知识基础、学习习惯为基点，以养成学生主动观察、善于发现的求知品质为出发点，以益于学生心智发展为落脚点.学案是教学艺术的再现，这种劳动具有创造性，凝聚着教师学习和实践的心血.