理解数学基础上的变式教学尝试

☉江苏省无锡市南长实验中学　胡晓红



理解数学基础上的变式教学尝试

☉江苏省无锡市南长实验中学胡晓红

现代教育强调“知识结构”与“学习过程”，目的在于发展学生的思维能力，而把知识作为思维过程的材料和媒介，把掌握知识、技能作为中介来发展学生的思维品质才符合素质教育的基本要求.教师“理解数学”的目的是让学生“理解数学”，这也是数学教学的主要任务.初中是学生的学习能力及创新和思维能力培养的关键阶段，具有较强的可塑造性，这一阶段创新意识、思维能力的培养，为学生以后的发展奠定了坚实的基础.因此，开发初中生的思维潜能，提高思维品质，具有十分重大的意义，而变式教学恰好提供了一个非常好的途径——为了达到“理解数学”的效果，变式教学在数学课堂中的应用就显得尤为重要.实际上变式教学作为连接双基与创新、知识与思维的纽带，已经被大多数教师在课堂上广泛应用.下面笔者就简单地谈一下在教学中运用变式教学的一点尝试.

一、理解教学内容间的联系，在概念体系中理解概念

在概念学习中，利用变式启发学生积极观察、分析、归纳，培养学生正确概括的思维能力.从培养学生思维能力的要求来看，学习数学概念时提示其内涵与外延，比数学概念的定义本身更重要，所以在形成概念的过程中，可以利用变式引导学生积极参与形成概念的全过程，利用变式让学生自己去发现不同概念之间的区别和联系，通过多样化的变式提高学生学习的积极性，培养学生的观察、分析及概括能力和思维的严谨性.

一节课的教学效果最终会如何，新知引入的方法起着关键作用，数学概念的教学亦是如此.在数学概念引入时就让学生接受变式训练，既可以拉近现实与概念两者的距离，也可以让学生对概念的最初印象更加准确和全面理解.

数学概念是一种延伸性比较强的理论知识，并且每一条概念都具有其自身的理论界限，只有使学生能够深入理解和掌握概念的规律，才能在实际应用中判断对象是否属于该界限范围内.所以说，实施变式教学的最佳措施就是将数学概念转化延伸为变异空间，以其对象为主要变式，并通过对拥有统一属性但类型不同的变式进行对比，从而突出该变式的特性.

问题：如图1，线段AB的长为2，C为AB上一个动点，分别以AC、BC为斜边，在AB的同侧作两个等腰直角三角形△ACD和△BCE，那么DE长的最小值是_______.

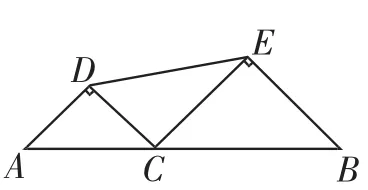
图1

思路1：代数法——建立函数关系式求解.

解法1：设AC=x，则BC=2-x.

由△ACD和△BCE都是等腰直角三角形，得∠DCA=45°，∠ECB=45°，DC=（2-x），所以∠DCE=90°.

则DE2=DC2+CE2=2=（x-1）2+1.

则当x=1时，DE2取得最小值，DE也取得最小值，最小值为1.

思路2：几何法——利用“垂线段最短”求解.

解法2：如图2，延长AD、BE交于点G，连接CG，则△AGB为等腰直角三角形，四边形GDCE为矩形，则DE=GC.

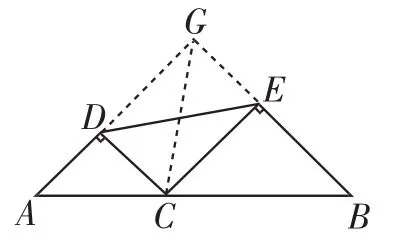
图2

评注：此解法通过添加适当的辅助线，将DE转化为GC，利用“垂线段最短”直接求解，避免了复杂的代数运算，较为简洁.

二、理解数学内容，弄清来龙去脉

学生对数学知识的认知不透彻，不能揭示问题的本质，造成思维的不完整性和模糊性，影响思维的发散创新性和聚合能力.如学生在解题过程中对某些解题方法的认知只是停留在表面上的理解，没抓住解题方法的实质，从而造成不能灵活应用的情况，这时可利用一题多解、一题多变、多题一解来设计变式题.回到上面的问题，从本质上进行深入挖掘，问题的解决会更直观.

解法3：如图3，作DF⊥AC于F，EG⊥BC于G，DH⊥EG于H，则DH=FG=AB=1.

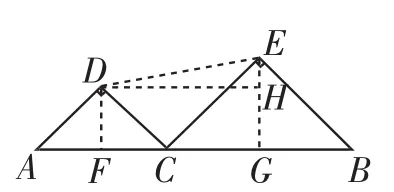
图3

显然DE≥DH，故DE的最小值为1.

评注：此解法通过添加适当的辅助线，利用“垂线段最短”直接求解，十分简洁.通过教师不断地点拨，揭示了知识的发生过程，把学生的思维自然地引到了知识发生和形成的轨道中，激发了学生积极观察、思考.在探索最佳解法中培养了学生的创造性思维.此时，为了提高对数学的理解水平，我们应当跳出问题的固然模式，从更加全面的角度来审视这个问题的结构和特点，于是在此基础上进行深入研究.

变式1：如图4，将原题中的两个等腰直角三角形△ACD和△BCE换成等边三角形，DE的长还存在最小值吗？如果存在，怎样求DE长的最小值呢？

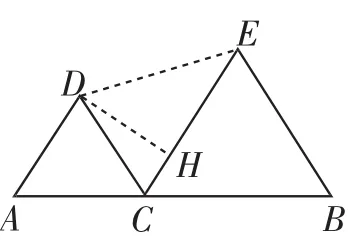
图4

仿上面解法1，可得答案.

解：设AC=x，则CD=x，CE=BC=2-x.作DH⊥CE于H，则CH=

则DE2=DH2+HE2=3（x-1）2+1.

则当x=1时，DE2取得最小值，即DE取得最小值，最小值为1.

仿解法3，还可简洁求解.

解：如图5，作DF⊥AC于F，EG⊥BC于G，DH⊥EG于H，则DH=

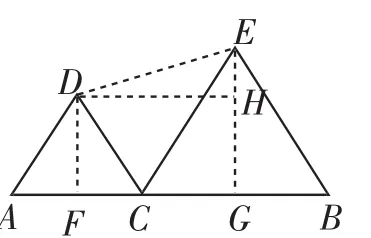
图5

显然DE≥DH，故DE的最小值为1.

变式2：如图6，将原题中的等腰直角三角形△ACD和△BCE换成分别以AC、BC为底的等腰三角形，DE的长还有最小值吗？怎样求DE长的最小值呢？

本题仿解法1、解法2均难以求解，但仿解法3，依然能简洁求解.

解：作DF⊥AC于F，EG⊥BC于G，DH⊥EG于H，则DH=FG=

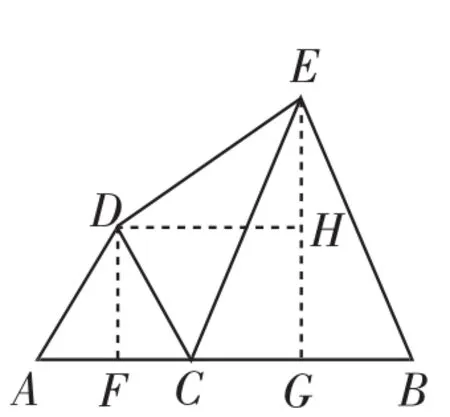
图6

显然DE≥DH，故DE的最小值为1.

一道练习，如果教师不进行深度加工，广度挖掘，学生得到的收获是有限的，解题思维也会逐步定势，再加上讲不得法，还会使学生产生错误的思维定势，若对例题的条件、结论进行变化，或改变题目的陈述，将会产生一种“新情景”，在此情景下进行变式训练，则对学生准确掌握知识与方法，提高他们的变通能力和创造性，促进认知结构的内化是相当有益的，于是提升层次的目标已经达到.

三、理解数学内容所反映的数学思想方法

一般地，数学思想是对教学对象的本质认识，是对具体的数学概念、命题、规律方法等的认识过程中概括的基本观点和基本想法，对数学活动具有普遍的指导意义.从上述问题中不难看出解法3利用“垂线段最短”直接求解具有一般性，同时仿解法3不难得到下列两个命题.

推广1：设线段AB的长为a，C为AB上一个动点，分别以AC、BC为底边，在AB的同侧作两个等腰三角形△ACD和△BCE，那么DE长的最小值是a.

推广2：设线段A2B1的长为a，C为A1B1上一个动点，分别以A1C、B1C为边，在A1B1的同侧作两个正（2n+1）边形A1A2…A2nC和B1B2…B2nC，那么An+1Bn+1长的最小值是a.

从上面这一系列的题目中，大家不难看出，一题多解，有利于沟通各知识的内涵和外延，深化知识，培养发散性和创造性思维；多解归一，有利于提炼分析问题和解决问题的通性、通法，从中择优，培养学生的聚合思维能力.从思维理论上看，一题多变是命题和解题方法的同时发散，一题多解是命题角度的集中、解法角度的发散，多题一解则是命题角度的发散、解法角度的集中，它能训练和培养学生的集中思维，揭示各方面知识的内在联系和规律，从而加深对各方面的理解和运用，使知识融会贯通.

变式教学可以促使学生的思维向多层次、多方向发散，帮助学生在问题的解答过程中去寻找解类似问题的思路、方法，有意识地展现教学过程中教师与学生数学思维活动的过程，充分调动学生学习的积极性，主动地参与教学的全过程，培养学生独立分析和解决问题的能力，以及大胆创新、勇于探索的精神，从而真正把学生能力的培养落到实处.

参考文献：

1.中华人民共和国教育部制定.义务教育数学课程标准（2011年版）［M］.北京：北京师范学大出版社，2012.

2.吕爱生.一则数学问题的解法再探［J］.中学数学教学参考（中），2014（10）.