基于ARMA-GARCH模型的同业拆借利率的VaR度量

何晓光

(珠三角科技金融产业协同创新发展中心，广东 广州 510320)



基于ARMA-GARCH模型的同业拆借利率的VaR度量

何晓光

(珠三角科技金融产业协同创新发展中心，广东 广州 510320)

摘要：以2007年1月4日至2013年12月31日CHIBOR和SHIBOR隔夜拆借数据为研究样本，建立基于ARMA-GARCH族的利率风险测度VaR模型，结论如下：t分布不适合描述隔夜拆借利率序列的分布状况；相对而言，GED分布假设更适合拆借市场多头头寸的风险预测，n-分布模型适合空头头寸VaR值的预测；隔夜拆借利率收益率都存在显著的波动非对称性，在利率上升时的波动更大，在利率下降时的波动会变小。

关键词：VaR模型；银行间同业拆借利率；利率风险；ARMA-GARCH模型

一、引言

利率市场化改革的不断推进，传统的利率敏感性缺口分析方法和持续缺口分析方法的缺陷将越来越不能满足现代商业银行利率风险度量的要求。我国金融业需要借鉴国际化的风险管理模式，引入先进的风险管理模式—VaR方法，对同业拆借利率的波动进行监测，并合理地估计与控制同业拆借头寸所面临的利率风险，中国人民银行可以通过运用VaR模型对各金融机构进行监管，商业银行则可以提高内部风险管理的技术水平。

赵武、王定成和曾勇(2011)[1]利用VaR方法建立了保险公司的最大风险承受能力与最优投资比例之间的关系，并给出了风险约束下保险公司的最优混合投资比例的最优解；杨夫立(2012)[2]对证券投资基金的市场风险进行了估计，认为基于GED分布的GARCH模型计算的VaR值最能真实反映基金的风险；房小定和吕鹏(2013)[3]认为GED分布较好地刻画了SHIBOR对数日收益率序列的分布；朱孟楠和侯哲(2013)[4]利用MFA-VaR模型对我国外汇储备面临的汇率风险进行了测度，认为在弱化各币种汇率波动相关性的条件下，我国外汇储备面临的汇率风险较小；何晓光和黄德权(2014)[5]研究了基于ARMA-GARCH簇的上海银行间同业拆借市场的多个市场利率风险测度VaR模型。

笔者认为有以下几点值得进一步讨论：1.CHIBOR是实盘交易形成的利率，交易规模小和活跃性低，而作为货币市场短期基准利率的SHIBOR是自主报价形成的，有必要作对比研究。2.SHIBOR数据自2007年1月4日才正式运行，采用最新最全的数据，可以准确反映市场的发展变化。3.少数学者直接利用利率而不是其收益率建立模型，准确性值得商榷。

二、理论模型

(一)VaR的计算

用GARCH模型估计波动率，资产持有者的多头头寸和空头头寸的日相对VaR模型分别为：

VaRt(α)=Pt-1εασt-1，VaRt(1-α)=Pt-1ε1-ασt-1

Pt-1、σt-1分别为SHIBOR的收益率拟合模型的条件均值和条件方差的向前一步预测值，εα、ε1-α为ε分布的左尾和右尾α分位数。

(二)CARCH模型簇

CARCH模型是GARCH模型的扩展形式，CARCH(1，1)模型是一个非线性的严格的GARCH(2，2)模型：

分别为短期和长期分量方程，ω是常数，qt将以速度λ1收敛于ω，z是外生变量，d是哑变量，当ut-1<0时，dt=1，否则dt=0；γ>0意味着条件方差中的短期杠杆效应，对长期波动率的影响主要体现在系数λ1的变化上。

(三)关于分布

对于GARCH模型簇中的残差分布，当正态分布假设不足以反映股市收益率序列的特性时，通常采用Nelson和Hamilton等人提出的t-分布和GED分布来拟合，GED分布的概率密度函数为：

当v<2时，GED表现为厚尾；当v=2时，GED为正态分布；当v>2时，GED则表现为瘦尾。

三、数据的基本特征

CHIBOR和SHIBOR是央行基准利率的重要参考指标，CHIBOR于1996年6月1日运行，交易规模小且活跃性低。2007年1月4日正式运行的SHIBOR，是由信用等级较高的银行组成报价团自主报出的人民币同业拆借利率确定的算术平均利率，SHIBOR是剥离了信用升贴水后的利率，CHIBOR是实盘交易形成的利率，两者生成机制有差异。为便于比较，选择2007年1月4日至2013年12月31日CHIBOR和SHIBOR的隔夜拆借数据进行实证研究。

(一)样本数据的处理

为得到平稳的收益率序列数据，对隔夜拆借利率数据分别计算了复合收益率，R1t=lnCHIBORt-lnCHIBORt-1，R2t=lnSHIBORt-lnSHIBORt-1，通过对数收益率的处理可以有效地消除原数列的自相关性。

(二)对收益率序列的检验

R1t和R2t的曲线图表明收益率序列无明显趋势，并呈现波动的异方差性，为合理选择模型，对CHIBOR和SHIBOR及其收益率序列进行正态性检验、平稳性检验、自相关性及条件异方差性检验。

1.拆借利率序列及其收益序列分布特征有差异。CHIBOR隔夜拆借利率从2007年到2013年12月的平均值达到2.362%，与SHIBOR的2.361%差异很小，都存在较大的波动性(CHIBOR与SHIBOR的标准差分别为1.169%、1.168%，反映了利率的波动性与投资者的高风险)。CHIBOR与SHIBOR的分布都呈现非对称性与右偏倚特征(偏度>0)，而R1t和R2t则呈现左偏倚特征(偏度<0)，分布峭度(Kurtosis)都显著大于3，表明了分布有厚尾特性。

2.拆借利率序列及其收益序列自相关性特征不同。CHIBOR和SHIBOR自相关图都呈现缓慢衰减特性，偏自相关图则呈现一阶截尾。而R1t和R2t自相关函数和偏自相关函数值差异不大，在5%的检验水平下，基本可以拒绝R1t和R2t不存在序列相关性的假设。

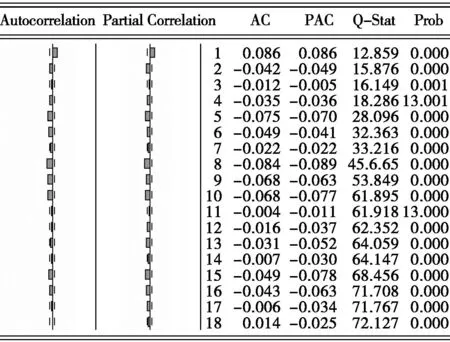
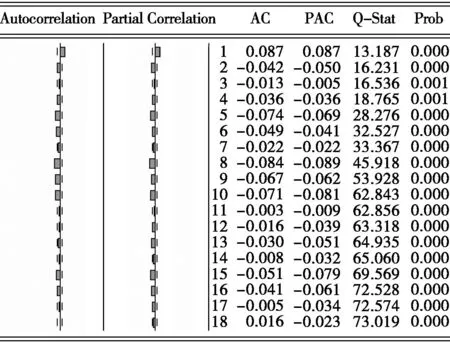
图1　CHIBOR和SHIBOR的收益率R1t和R2t序列相关图

3.拆借利率序列及其收益序列平稳性特征不同。对收益序列分别进行了单位根检验的ADF(Augmented Dickey-Fuller Test)检验、PP(Phillips-Perron)检验，结果发现拆借利率序列属不平稳序列，R1t和R2t序列则属平稳序列，通过运用LM检验，证实R1t和R2t序列是自回归条件异方差过程。

因此，以R1t和R2t为因变量，采用ARMA与 GARCH类模型相结合来估计和预测同业拆借利率的波动性。

四、实证分析与模型检验

(一)各种分布假设下Rt的ARMA-GARCH模型簇估计

表1　收益率序列R1t和R2t在不同分布假设下的优选模型

对序列Rt分别假设模型残差序列服从n-分布、t-分布和g-分布，基于AIC、SC值以及残差检验的相伴概率，并考虑到模型系数的显著性水平，以此确定模型的滞后阶数，经过反复测算，最终为序列R1t和R2t分别选择了5种刻画其时变性特征的条件异方差模型，各模型能较好地描述同业拆借利率收益序列的异方差现象，具体优选模型见表1(限于篇幅，具体拟合参数略)。

(二)VaR模型的回测检验

在不同的分布及置信度下，计算出CHIBOR和SHIBOR市场的VaR结果，分别见表2、表3，所构建的VaR模型是否有效，需要采用回测技术来检验VaR模型的准确性。采用的回测检验方法是由Kupiec(1995)提出的基于失效率的似然比率验证方法，检验统计量为：

在零假设成立条件下，统计量LR服从自由度为1的卡方分布，其95%置信水平下的分位数为3.841，当在95%置信水平下计算VaR时，如果此时的LR>3.841，我们就拒绝模型，LR统计量的值越小，说明该模型的预测越准确。

表2　置信度为 95%的R1t各模型日相对VaR的统计结果

注：*表示在显著性水平为5%时，数据通过了自由度为1的卡方分布，从而可以接受原模型。

表3　置信度为 95%的R2t各模型日相对VaR的统计结果

注：*表示在显著性水平为5%时，数据通过了自由度为1的卡方分布，从而可以接受原模型。

对隔夜拆借利率，CHIBOR和SHIBOR的风险度量具有相近的结果，即在相同新息分布假设和相同的显著性水平下，各模型计算得到的多头头寸和空头头寸的VaR估计的失败天数无明显差异。而在不同分布假设和不同的显著性水平下，返回测试的结果却出现了明显的差异。在正态分布假设下，多头头寸的VaR值偏高，失败率偏低，显得过于悲观，而空头头寸的VaR估计值比较理想。相对于正态分布新息假设而言，GED分布假设下的空头头寸的VaR值偏小，失败率偏高，而多头头寸的VaR估计值比较理想。

五、结论

第一，通过选择适当的滞后阶数和新息假设，两种隔夜拆借利率的收益率序列都可以通过ARMA-GARCH模型簇来刻画，通过分析各模型中反映波动的非对称性特征的具体参数可知，隔夜拆借利率收益率都存在显著的波动非对称性，但又非杠杆效应，在利率上升时的波动更大，在利率下降时的波动会变小。

第二，在新息相同分布假设和相同的显著性水平下，不同的GARCH模型簇计算得到的VaR值并无明显差异，失败天数相差不大，而在不同分布假设和不同的显著性水平下，返回测试的结果却出现了明显的差异，说明模型种类的选择并非VaR值度量的关键因素，而VaR更关注尾部特征。

第三，分布假设和显著性水平的高低影响VaR值的准确性。由于在t-分布假设情况下，没有合适的模型能够拟合收益率，说明t-分布假设不符合市场利率的新息特征；对多头头寸而言，GED分布新息分布假设优于正态分布假设和t-分布假设；正态分布假设虽然能够比较理想地估计空头头寸的VaR，但却会高估多头头寸的风险值。

[参考文献]

[1]赵武，王定成，曾勇.基于VaR风险约束下保险公司的最优混合投资策略[J].统计与决策，2011(12)：57-60.

[2]杨夫立.基于GARCH模型的证券投资基金VaR计算与实证研究[J].经济问题，2012(6)：87-91.

[3]房小定，吕鹏.基于GARCH模型的上海同业拆借利率风险度量[J].西安电子科技大学学报，2013(4):18-26.

[4]朱孟楠，侯哲.中国外汇储备汇率风险损失区间测度——基于重新定义下的研究[J].财贸经济，2013(8)：58-66.

[5]何晓光，黄德权.基于ARMA-GARCH类模型的上海银行同业拆借利率VaR比较[J].经济与管理评论，2014(9)：38-43.

(责任编辑：董博雯)

中图分类号：F832.1

文献标识码：A

文章编号：2095-3283(2016)02-0085-03

[基金项目]本论文的研究工作受珠三角科技金融产业协同创新发展中心资助。

[作者简介]何晓光(1970-)，男，河南新县人，广东财经大学金融学院副教授，博士，研究方向：数量经济学与金融经济学。