一类二元函数值域求法的探究
一类二元函数值域求法的探究
许正
(江苏省江阴高级中学,214443)
二元函数值域问题是高中数学常考的题型,学生在遇到此类题型时,往往错误率较高.本文先介绍一些解决此类问题的几种基本解法,如消元法、不等式法、向量法、三角换元法、化归法等,再通过变题介绍一些特殊解法,从而让学生能更有效地解决此类问题.下面笔者就从几个例题出发系统阐述这类问题的解决方法.希望对学生有所启发.
例1已知a,b>0且ab=a+b+3.
(1)求ab的取值范围;
(2)求a+b的取值范围.
思路1由条件可知a,b∈R*,所以想到基本不等式,通过已知的条件等式构造关于ab和a+b的不等式.
思路2消元转化为一元函数的值域问题(注意自变量范围的求解).
解法1(不等式法)
(1)∵a,b>0,

当且仅当a=b时取等号.
由条件可得

解得ab≥9.
(2)由(1)可得a+b=ab-3≥6.
解法2(消元法)
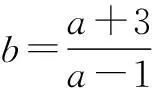
变题已知a,b>0且ab=a+b+3,求a+2b的取值范围.
分析很明显此题已经不能使用不等式的解法了,所以不等式法不能解决所有不等式问题,但可用消元法解决.
例2已知x2+xy-y2=1,求t=2x+y的取值范围.
分析我们发现以上介绍的方法都不能解决这个二元函数值域问题,我们可以采用化归的思想方法把这个问题转化为一个二元方程有解的问题,即可解决.
解由t=2x+y,得y=t-2x,代入题设条件等式得
x2+x(t-2x)-(t-2x)2=1,整理得
5x2-5tx+t2+1=0,
则原问题等价于此方程有解,故Δ≥0,即得t≥2或t≤-2.

思路1我们发现根号下的和是定值,可以利用向量的工具解决.


z=m·n=|m||n|cosθ
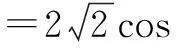


上题还可用两边同时平方的方法解决,若只是要求其最大值还可用基本不等式法,三角换元、柯西不等式等方法直接求得,留由读者练习.
例4已知变量x,y满足条件
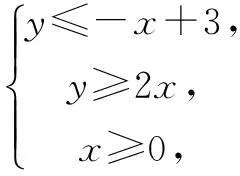

例5已知m,n∈R,且m+2n=2,则m·2m+n·22n+1的最小值为______.
分析此题可看作二元函数的值域问题,通过条件可先消元转化为一元函数,可设一元函数为f(x)=x·2x+(2-x)22-x,再由函数单调性即可求得最小值.
解(构造函数)令m=x,f(x)=x·2x+(2-x)22-x易知f(x)=f(2-x),则f(x)图象关于x=1对称.
当x>1时,
f′(x)=x2xln 2+2x-(2-x)22-xln 2-22-x
=(2x-22-x)+ln 2[x2x-(2-x)22-x].
易知函数y=x2x与y=2x均为增函数,故x>1时x>2-x,∴f′(x)>0,即f(x)是增函数,由对称性可知x<1时f(x)递减,所以f(x)min=f(1)=4,从而原式的最小值为4.
二元函数的值域是高中数学中的常考的重难点,本文通过系统的解题方法介绍了解决此类问题的常用方法,希望对读者有所启发.

