平凡中显创意 朴实中见功夫───一道高考数学试题的探究与感悟



平凡中显创意朴实中见功夫
───一道高考数学试题的探究与感悟

芮国英钱军先

(无锡市辅仁高级中学，214123)

随着新课程的实施和不断深入,经过多年的探索,高考数学命题已从理论和实践上发生了深刻的变化,落实新课程的基本理念,体现数学的本质特征,以问题为背景,以知识为载体,以方法为依托,以能力为主线,已成为高考数学命题的主流.综观全国各地的高考数学试题,表述简洁,设计新颖,情境交汇,知能并重,既引导教学、又利于选拔的创新试题精彩粉呈、举目可见.本文以2012年江苏省高考数学试卷第14题为例,作一些探究,谈一点感悟.

一、考题赏析

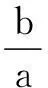
这道试题以不等式为背景,以线性规划的知识和方法为载体,以新颖的视角和创新的手法,在不等式、线性规划、对数运算、导数、等价转化、数形结合等基础知识和基本数学方法的交汇处精心设计,文字表述简洁明了,题给条件简单清晰,构思巧妙,不落俗套,较好地彰显了新课程的理念,实现了对数学知识、数学方法和数学思想的多角度、多层次的考查,有效地甄别了学生的思维水平和数学潜能,是一道内涵丰富、匠心独具、在平凡中显创意、在朴实中见功夫的好题.

二、解法探究

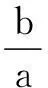
解法1条件5c-3a≤b≤4c-a,clnb≥b+clnc可化为

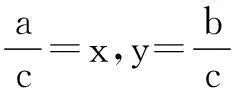
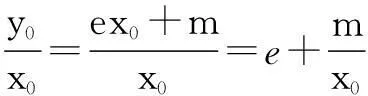
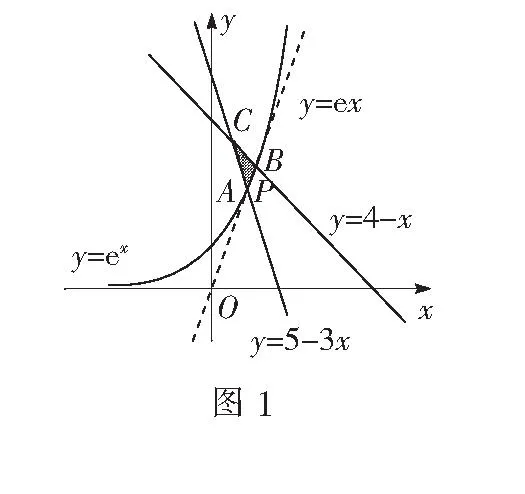
解法2由题意知a, b, c>0,在不等式5c-3a≤b≤4c-a两边同除以正数a,可得

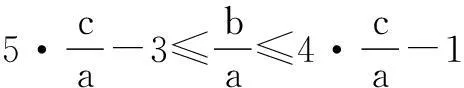
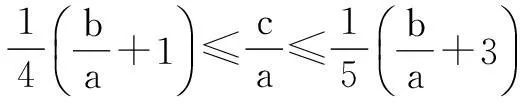
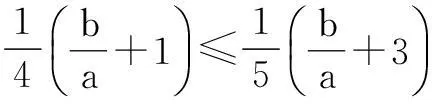
又由clnb≥a+clnc,得

clnb-clna≥a+clnc-clna,

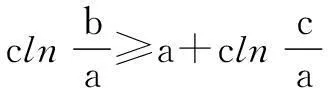
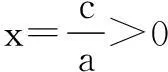
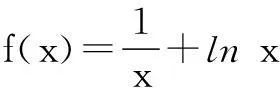
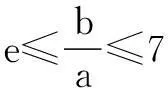
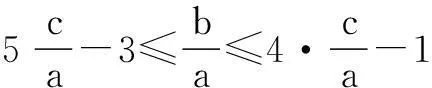
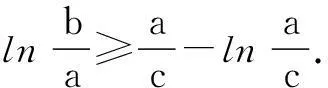
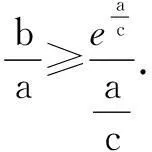
三、题源追溯

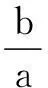
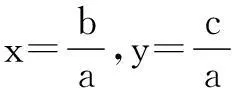
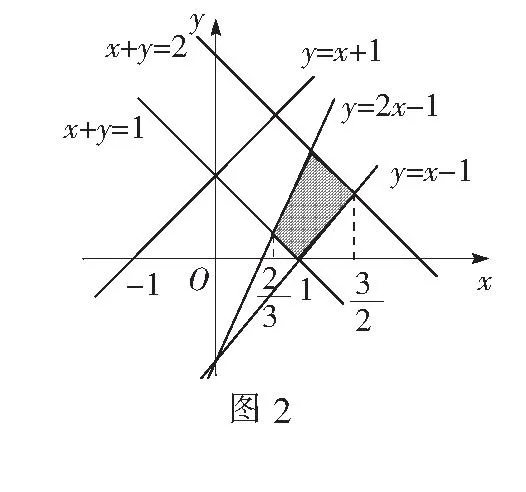
作出可行域,如图2所示.

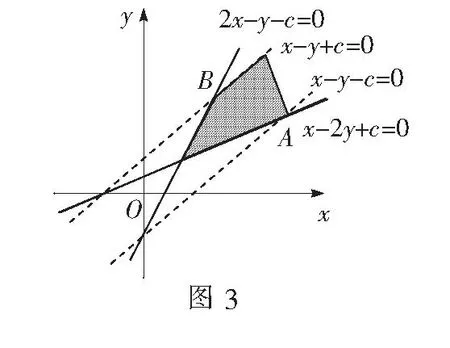
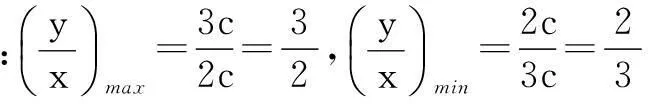
可以说,苏州大学高中数学《教学与测试》(教师用书,2011版)第232页的例2是2012年江苏省高考数学试卷第14题的题源,而2012年江苏省高考数学试卷第14题则是在苏州大学高中数学《教学与测试》(教师用书,2011版)第232页例2的基础上经过加工改造、变式引申而成的,这正是高考数学命题时常用的基本手法之一.

四、教学感悟

我们的老师常会有这样的困惑:类似的问题讲过多遍,学生在复习的过程中也练习了相当多的习题,为什么在考试时还是经常举步维艰、错误百出呢?以本文中的高考试题为例,苏州大学的复习资料很多学校都在使用,第232页的例2,相信绝大多数的老师在组织复习时肯定会重点讲解,然而学生在高考中解答本题的表现并不好,解对此题的考生屈指可数.问题出在哪里呢?笔者以为:这与我们在实施复习教学时,受“应试本位教学观”的影响而产生的浮躁作风──“急功近利”及其相应的一些教学行为有关.

由于近几年来的高考数学试卷的结构、题型和难度相对稳定,我们的老师们积累了

丰富的应试经验,在复习教学中为了赶进度,过多地凭借经验想当然,试图让学生在多听讲、多接触、多训练中达到“熟能生巧”,不求知识能力的迁移同化,不求思想方法的融会贯通,但求常规题型的“熟与会”,忽视数学问题的本质,大搞题海战术,反复地“练──讲──练”,压缩学生独立思考、交流讨论的时间和空间,使学生的思维停留在机械操作、外部感知的层面,难以在头脑中实现认知结构的重组,形成良好的思维习惯和方式,致使他们在独立且紧张的高考环境下,面对“新情境、新问题”时被套牢,甚至是对于仅在条件或结论上稍稍作了一些调整的变式问题,也会显得一筹莫展、束手无策,从而造成无尽的遗憾.

数学是研究数量关系和空间形式、揭示自然规律的科学,是一门充满生机与活力的学科.高考试题千变万化,但万变不离其宗.高考数学考什么?简单地说就是四考:考基础知识、考思想方法、考思维能力、考数学应用.这就要求我们在高三数学的复习教学中,跳出题海,重视基础知识,突出通性通法,采用“低起点、全方位、多层次、快反馈”的方式,多对学生实施原型启发和变式训练,进行创造性教学,重导轻授、重学轻讲、重思维轻题型、重过程轻结果、重思想轻记忆,让学生理解数学概念,把握数学方法,体会数学思想,抓住数学的本质,学会数学特有的思维方式,真正提高学生的数学素养.只有这样,才能有效地培养学生分析问题、解决问题的能力,从而在高考中做到随机应变,取得理想的成绩.