谈构造立体几何模型解题



谈构造立体几何模型解题

由国清

(辽宁省建平县职业教育中心，122400)

在解决数学问题时，我们常常采用构造法.在运用构造法解题时，可以针对具体问题构造不同的数学模型，如函数、方程、向量等等，也可以构造图形，如构造立体模型.为增强学生的发散思维能力,在解题方法上加以创新,笔者在教学时发现,有些问题通过构造立体模型来解决,会收到事半功倍的效果.本文在从以下几个方面作出尝试,以便抛砖引玉．

一、求函数的最值

分析函数f(x)可化为

构造如图1所示的长方体,其棱长分别为AB=2，BB1=5，BC=3.设BE=x则

f(x)=AE+EC1.

二、证明三角不等式

例2已知αβγ均为锐角,且cos2α+cos2β+cos2γ=1，求证tanα+tanβ+tanγ.

分析长方体的一条对角线与过同一顶点的三条棱所成角的余弦值的平方和等于1,为此我们可构造一个相应的长方体ABCD——A1B1C1D1(如图2),使∠C1AD=α，∠C1AB=β，∠C1AA1=γ.设AD=a,AB=b,AA1=c，则

∴tanα+tanβ+tanγ

当且仅当a=b=c时取等号.

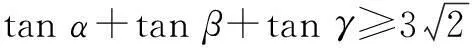
三、证明代数不等式

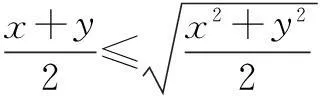
例3设x，y为正数,求证:

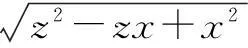
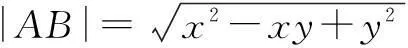
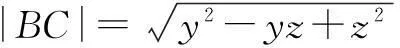
在∆ABC中，显然有不等式|AB|+|BC|>|AC|，故原不等式成立．

四、在几何中构造模型

例4如图4，正四面体O—ABC的各棱长均为1,点D,E分别为棱OA,BC的中点.

(1)求DE的长；

(2)点O到平面ABC的距离．

分析由于正四面体可以放在正方体中得到,所以,我们可以将正四面体O—ABC放到一个正方体中，如图5所示.

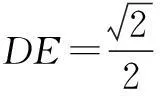
(2)求点O到平面ABC的距离,可以采用等积法，即

VO-ABC=V正方体-4VG-OAB.

设点O到平面ABC的距离为h,则

本文从四个方面阐述了利用构造几何模型的来进行解题.构造几何模型能使问题从一般到特殊,从抽象到具体,从陌生到熟悉,是一种化难为易的解题思想．这类题型不仅开阔学生的视野,而且还有助于发展学生的发散思维能力,提高学生学习数学的热情,为今后学习打下良好的基础．