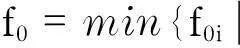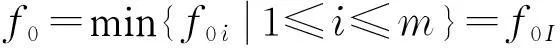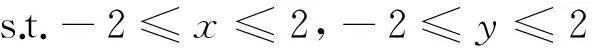求解非光滑优化问题的改进大洪水算法

张清叶,　高　岩,　马　良

(上海理工大学 管理学院,上海　200093)



求解非光滑优化问题的改进大洪水算法

张清叶,高岩,马良

(上海理工大学 管理学院,上海200093)

摘要：应用启发式算法求解非光滑优化问题,解决基于次梯度信息的确定性算法在求解时困难较大的问题.首先分析了基本大洪水算法的优化机理及特征并给出其求解步骤,然后针对无约束及盒子约束问题分别设计了改进的大洪水算法,将基本大洪水算法所依赖的参数up省去.对于无约束情形,提出了进行邻域搜索的随机行走法;对于盒子约束情形,提出了选择初始可行点的方法和进行邻域搜索的混沌优化算法.最后通过算例进行测试并与其他算法进行对比,测试结果表明了改进的大洪水算法在求解非光滑优化问题时的有效性与优越性,故其可作为求解非光滑优化问题的一种实用方法.

关键词：大洪水算法; 非光滑优化; 随机行走; 混沌

非光滑优化广泛应用于经济、力学、工程和最优控制等众多领域,然而由于不具有连续可微性质,基于梯度信息的经典优化方法不再适用.目前,次梯度法和束方法是求解非光滑优化问题最常用的两种方法[1-2],但由于凸函数的次梯度与局部Lipschitz函数的广义梯度计算困难较大,从而严重影响了非光滑优化算法的应用.鉴于非光滑优化问题的普遍性及计算的困难性,本文拟引进启发式算法对其进行处理.

大洪水算法(great deluge algorithm,GDA)是一种受自然界启发的优化算法,它通过模拟洪水的上涨过程来进行全局寻优,该算法最早由Dueck于1993年提出[3].Dueck在利用threshold accepting(TA)算法进行实验时,发现了两个行之有效的启发式算法,其中之一便是大洪水算法.它与模拟退火算法[4](simulated annealing,SA)有着相似的结构,但在迭代过程中对劣解的接受规则不同,且比模拟退火算法依赖于更少的参数.由于其遍历过程与圣经中诺亚方舟的大洪水有相似之处,故称之为大洪水算法.其算法思想可描述为:设想有一块崎岖不平的空地,在这块空地上一直不间断地下雨从而产生洪水,空地上有一个人,他可以向任意方向移动,然而随着水平面不断上涨,为了生存,此人必须不断地移至更高处,一段时间之后,此人最终将到达空地的最高点,即最大化问题的最优解.对于最小化问题,有两种处理方法:其一是将目标函数取负值,从而将最小化问题转化成最大化问题;其二是修改大洪水算法,不妨称为干旱算法,寻找高处的人为寻找水的鱼类代替.

Dueck首先将大洪水算法用于旅行商问题(traveling salesman problem,TSP)的求解,随后国内外一些学者对大洪水算法进行了研究[5-10],如将其应用于二次分配、电力调度、复杂系统可靠性等问题的求解中.然而,截至目前尚未有学者将其用于求解非光滑优化问题.

本文接下来给出基本大洪水算法的求解步骤,然后针对无约束及盒子约束非光滑优化问题分别设计改进的大洪水算法,同时给出相应的伪代码,最后通过算例对所给算法进行测试.

1基本大洪水算法的求解步骤

以最大化目标函数f(x)为例,其中f(x)是n上的实值函数,即求解f(x).

算法1基本大洪水算法(BGDA)

Step1初始化

给定初始可行解x0,计算f(x0);

设置初始水平面高度water_level,令water_level:=f(x0);

设置水平面上升速度up>0;

设置迭代次数上界count,置迭代因子i:=1;

fori=1:count,执行Step2.

Step2优化

在x0附近进行邻域搜索,得新解x,计算f(x).

执行if判断语句:

iff(x)>water_level,则

置x0:=x,water_level:=water_level+up.

Endif

迭代因子i增加1,即令i:=i+1.

Endfor

Step3输出x0,f(x0).

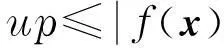
2针对无约束优化问题的算法

考虑问题

(1)

其中f(x)不一定连续可微.由于无约束,可在n中任选一点作为初始解x0,然后利用随机行走法[11]进行邻域搜索.不妨设迭代进行到第k步,当前解为xk,设置迭代格式,令xk+1=xk+λkdk,其中λk为邻域半径,dk为规划后的搜索方向.为使dk能遍历所有方向,可随机生成多个[-1,1]之间的n维向量,其中n为决策变量x的维数.注意到在基本大洪水算法的求解步骤Step 2中,对water_level的更新准则依赖于参数up,改进算法将参数up省去,更新准则采用water_level=f(x),这样一方面可以减少参数,另一方面通过大量测试发现运行效率可得到较大提高.下面给出求解问题(1)的具体步骤,按伪码形式叙述如下.

算法2无约束优化问题的改进大洪水算法,(UCGDA)

Begin

给定x0,计算f(x0),设置初始水平面高度water_level,令water_level:=f(x0);

设置迭代次数上界count,设置邻域搜索时生成搜索方向个数m,置迭代因子i:=1;

进入for循环,fori=1:count.

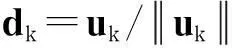
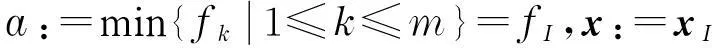
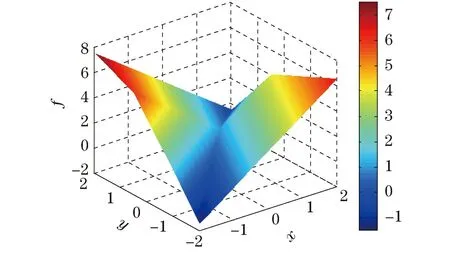
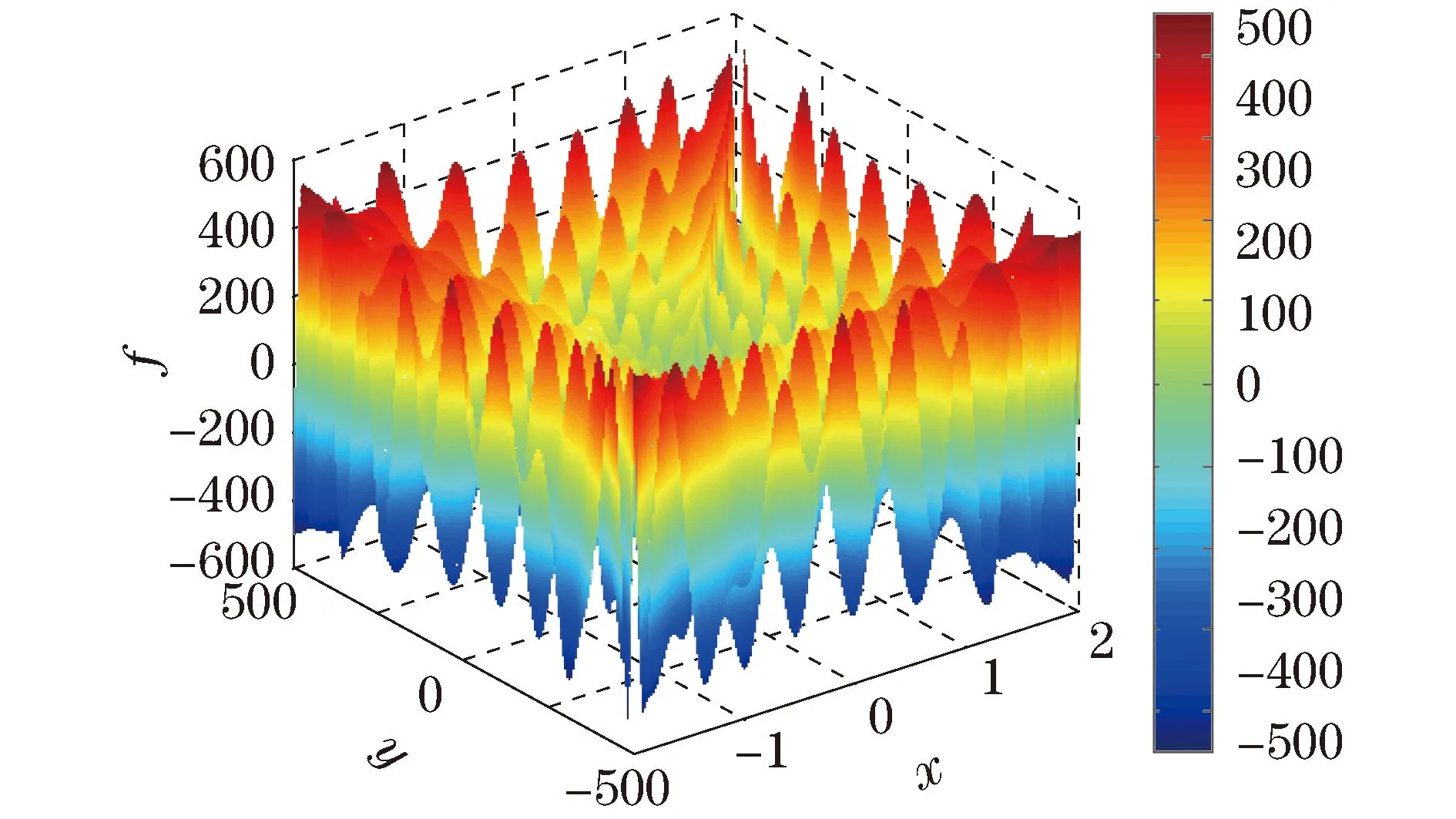
执行if判断语句:ifa

置x0:=x,water_level:=a.

Endif

迭代次数增加1,即令i:=i+1.

Endfor

输出最优解x0和最优值water_level.

End

算例测试

为验证算法的有效性,下面选几个测试函数进行求解,并将求解结果与用模拟退火算法、Matlab优化工具箱命令fminsearch所得结果进行对比.表1列出了当前能找到的最优解x**和对应的最优值f**=f(x**),表2列出了各种算法求得的最优解x*与对应的最优值f*=f(x*).上述3种算法均在Win7系统Matlab2012a环境下实现.参数设置如下:算法2(UCGDA)迭代上界count取1 000,邻域半径λ取0.1,邻域搜索时搜索方向个数m取100;模拟退火算法与fminsearch的参数设置取工具包默认值,初始点为相同初始点.

例1wolfe函数

初始点设为x0=(3,2)T.

例2Rosen-Suzuki函数

初始点设为x0=(0,0,0,0)T.

例3Spiral函数

f(x)=max{f1(x),f2(x)}

初始点x0=(1.411 831,-4.794 62)T.

表1　当前最优解

表2　求解结果

通过对表2的求解结果进行分析可以发现,UCGDA的求解精度均优于SA.此外,由于fminsearch为局部搜索算法,其求解结果严重依赖于初始点的选取,当初始点选取不太合适时,将产生较大误差,如例2.而在实际问题中,由于最优解是待求的,初始点的选取大都是盲目的,故为得到全局最优解应使用UCGDA.综上,为得到质量较好的全局最优解,算法2不失为求解非光滑无约束优化问题的一种实用方法.

为进一步加快算法收敛速度,在对water_level进行更新时,亦可令

water_level=min{water_level+up,f(x)},其中,up<0为水平面下降速度.

3针对盒子约束优化问题的算法

考虑问题

(2)

式中,x,a,b均为n维向量,f(x)不一定光滑.

另一种方法则是不进行转化,直接对约束优化问题进行求解.本文拟设计专门针对约束优化问题的改进大洪水算法.

不妨在盒子G内任取一点x0作为初始解,其函数值f(x0)作为初始水平面,设置up值及迭代次数上界count.在邻域搜索时,所求解x不仅需在x0附近,还需在G内.为得到函数f(x)在盒子G内的全局最优解,希望邻域搜索时能遍历G内的所有点且最好不重复,而混沌恰好具有此性质,故在求解约束优化问题时,可考虑采用Logistic映射产生混沌序列.

混沌是一种普遍的非线性现象,其行为复杂且类似随机,但有精致的内在规律性.混沌优化算法是一种全局优化算法[9,12],其理论基础是混沌的遍历性.混沌优化是通过混沌变量来实现的,混沌变量的产生有多种方法,如应用广泛的Logistic映射,其方程为ti+1=μti(1-ti),i=1,2,…,其中μ为控制参数,0≤ti≤1,当μ=4时处于完全混沌.

设函数优化变量x(a≤x≤b)为n维向量,T={t1,t2,…}为Logical映射函数产生的混沌序列,其中ti(i=1,2,…)亦为n维向量且满足

(3)

式中:.*表示两个向量的对应元素相乘,其结果为一n维向量;0表示元素全为0的n维向量;1表示元素全为1的n维向量.x与T取值的映射与逆映射公式为

(4)

(5)

即xiti→ti+1xi+1→ti+2xi+2→ti+3→…,其中,./表示两个向量的对应元素相除,其结果为一n维向量.

算法3(盒子约束优化问题的改进大洪水算法,BCGDA)

Begin

设置初始水平面高度为water_level,令water_level:=f0;

设置迭代次数上界count,置迭代因子i:=1;

进入for循环,fori=1:count.

按式(3)由ti生成ti+1,按式(5)将ti+1映成xi+1,计算f(xi+1).执行if判断语句:

iff(xi+1)

置x0:=xi+1,water_level:=f(xi+1).

Endif

迭代次数增加1,即置i:=i+1.

Endfor

输出最优解x0和最优值water_level.

End

算例测试

同算法2一样,为验证其有效性,下面选几个测试函数进行求解,并将求解结果与用模拟退火算法、Matlab优化工具箱命令fmincon所得结果进行对比.表3列出了目前能找到的最优解x**和最优值f**=f(x**),表4列出了各种算法的求解结果x*和f*=f(x*).参数设置如下:算法3(BCGDA)迭代上界count取1 000,为加快收敛速度,在算法初始化阶段,在可行域G内随机生成100个点,即取m=100;模拟退火算法与fmincon的参数设置取工具包默认值,初始点为相同初始点.

表3　当前最优解

表4　求解结果

例4

曲面图如图1所示.

例5

s.t.-512≤x≤512,-512≤y≤512

曲面图如图2所示.

图1　例4曲面图

图2　例5曲面图

这里需要指出的是,模拟退火算法与fmincon的运行结果与初值关系非常密切,给定不同的初值将得到不同的结果.为了得到较好的结果,首先在G内任取100个点,从中筛选出最优点作为初始可行点,例4中取x0=(0,0)T,例5取x0=(-502.582 9,482.484 5)T.算法3对初值不敏感,给定不同初值,均能得到最优解.

4结束语

本文针对无约束及盒子约束非光滑优化问题提出了改进的大洪水算法,去掉了大洪水算法所依赖的唯一参数up,对无约束情形在进行邻域搜索时提出了随机行走算法;对约束优化问题为加快算法收敛速度,给出了选择初始可行点的方法,在进行邻域搜索时引入了混沌优化算法.通过对大量算例进行测试,发现本文提出的改进大洪水算法是求解非光滑优化问题的一种切实可行的方法.此外,虽然本文所提算法是针对非光滑函数给出的,但在实际应用中,任何非线性规划问题均可用之求解.为进一步验证算法的可行性及优越性,对文献[9]所给算例进行了测试,结果发现本文所给算法能较快收敛到最优解.如何将大洪水算法推广至带复杂非线性约束非光滑问题的求解上,以便进一步扩大其应用范围,是一个值得考虑的问题.

参考文献：

[1]高岩.非光滑优化[M].北京:科学出版社,2008.

[2]王伟伟,高岩.凸可行问题的一种次梯度投影算法[J].上海理工大学学报,2009,31(5):422-426.

[3]Dueck G.New optimization heuristics:the great deluge algorithm and the record-to-record travel[J].Journal of Computational Physics,1993,104(1):86-92.

[4]Eglese R W.Simulated annealing:a tool for operational research[J].European Journal of Operational Research,1990,46(3):271-281.

[5]魏欣,马良,张惠珍.二次分配问题的大洪水算法求解[J].运筹与管理,2011,20(1):12-15.

[6]Lenin K,Reddy B R,Kalavathi M S.An improved great deluge algorithm(IGDA)for solving optimal reactive power dispatch problem[J].International Journal of Electronics and Electrical Engineering,2014,2(4):321-326.

[7]Ravi V.Optimization of complex system reliability by a modified great deluge algorithm[J].Asia-Pacific Journal of Operational Research,2004,21(4):487-497.

[8]Al-milli N.Hybrid genetic algorithm with great deluge to solve constrained optimization problems[J].Journal of Theoretical and Applied Information Technology,2014,59(2):385-389.

[9]盛虹平,马良.混沌大洪水算法求解函数优化问题[J].计算机应用研究,2011,28(5):1626-1627.

[10]Kifah S,Abdullah S.An adaptive non-linear great deluge algorithm for the patient-admission problem[J].Information Sciences,2015,295:573-585.

[11]吴鹏.Matlab高效编程技巧与应用:25个案例分析[M].北京:北京航空航天大学出版社,2010.

[12]王秀梅,秦体恒.基于混沌优化算法的最小二乘圆参数估计[J].武汉理工大学学报,2008,30(8):101-104.

(编辑:丁红艺)

Improved Great Deluge Algorithm for Nonsmooth Optimization Problems

ZHANG Qingye,GAO Yan,MA Liang

(Business School,University of Shanghai for Science and Technology,Shanghai 200093,China)

Abstract：Since nonsmooth optimization problems are difficult to solve by deterministic algorithms based on subgradient information,the heuristic algorithm was considered.The optimization mechanism and characteristics of the basic great deluge algorithm(GDA)were analyzed and the solving steps were given as well.Then improved GDAs for unconstrained and box constrained problems were proposed respectively,where the parameter up was omitted.For the unconstrained case,the random walk algorithm with respect to neighborhood search was proposed.For the box constrained case,the method of choosing a feasible initial point and a chaos optimization algorithm with respect to neighborhood search were proposed.The improved GDAs were tested by taking several typical nonsmooth optimization problems as examples and were compared with other algorithms.The test results show that the improved GDAs are efficient and superior to other algorithms mentioned in the paper.So it can be used as a practical method for solving nonsmooth optimization problems.

Keywords：great deluge algorithm; nonsmooth optimization; random walk; chaos

中图分类号：O 224

文献标志码：A

通信作者：高岩(1962-),男,教授.研究方向:非光滑优化、投资组合优化、混杂系统控制.E-mail:gaoyan@usst.edu.cn

基金项目：国家自然科学基金资助项目(11171221);高等学校博士学科点专项科研资助项目(20123120110004);上海市一流学科建设资助项目(XTKX2012)

收稿日期：2014-12-01

DOI：10.13255/j.cnki.jusst.2016.01.008

文章编号：1007-6735(2016)01-0043-05

第一作者： 张清叶(1978-),女,博士研究生.研究方向:非光滑优化、投资组合优化.E-mail:zhangqingye123@163.com