非线性耦合Harry-Dym方程的对称约化

胡　潇,　胡恒春

(上海理工大学 理学院,上海　200093)



非线性耦合Harry-Dym方程的对称约化

胡潇,胡恒春

(上海理工大学 理学院,上海200093)

摘要:借助符号计算软件Maple将Clarkson-Kruskal直接法应用于非线性耦合Harry-Dym方程中,运用相应规则得到对称变换并求得非线性耦合Harry-Dym方程的相似变量和相似解.通过选取不同的特殊常数得到非线性耦合Harry-Dym方程两种常微分形式的对称约化方程.利用约化方程构造了非线性耦合Harry-Dym方程可能的新严格解.

关键词:对称约化; Clarkson-Kruskal直接法; 非线性耦合Harry-Dym方程

1问题的提出

众所周知,孤立子理论是非线性科学的重要组成部分.一般来说,孤立子理论的研究对象大多数是非线性系统,这些非线性系统可以描述流体力学、等离子物理学、非线性光学及环境科学等领域出现的某些非线性现象.因此,对非线性系统的精确求解问题在理论上和应用上都具有重要的研究意义[1-2].近年来,经过数学家和理论物理学家的不懈努力,提出了许多行之有效的构造非线性系统精确解的方法,如反散射方法、贝克隆变换法、tanh-coth展开方法、广田双线性法、分离变量法、达布变换法及李群方法等.

由于非线性系统不满足解的线性叠加原理,人们很难求出它们所有的精确解．因此,需要寻求一些简单的方法来简化复杂的非线性系统,使之转化为低维的偏微分方程或常微分方程,通过求解低维的偏微分方程或常微分方程,进而得出原来非线性系统的精确解．

本文主要研究非线性耦合Harry-Dym方程,简称cHD方程,其形式为

(1)

式中,p为常数.

2方法简介

人们对偏微分方程的对称性研究主要包括寻找方程所允许的对称群、对称约化和群不变解[10].寻找偏微分方程对称约化的方法有很多,其中主要有以下3种方法:a.Lie的经典无穷小变换法[11];b.Bluman和Cole的非经典无穷小变换法[12];c.Clarkson和Kruskal提出的CK直接法[13-14].

1989年Clarkson和Kruskal首次提出的CK直接法是用来推导非线性偏微分方程的相似约化的直接方法,这是一种不涉及群论的直接约化方法.Clarkson和Kruskal用这种方法最先求解的是Boussinesq方程[13],得出很多不同于用经典无穷小变换和非经典无穷小变换方法求出的相似解.1990年Lou[14]完善了这种方法,并且推广到(2+1)维KP方程中,获得了一些相似解.之后，这种方法被推广应用于方程组等其他一大批非线性方程[15-16].2000年Lou提出了条件约化的概念[17],并用直接约化法的思想获得了(2+1)维KdV方程的6种新的条件相似约化,该条件相似约化不能由现有非古典理论推得.

对于非线性偏微分方程

(2)

直接寻找偏微分方程如下形式的相似解：

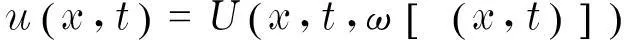
(3)

式中,函数U,ξ待定.

这是最一般的相似约化的形式.将式(3)代入式(2)中,要求结果是关于ω的低维偏微分方程或常微分方程,附加条件与U,ξ及它们的导数有关,而后能够进一步解出U,ξ的具体形式.

对于一般低维对称性约化,可以选取

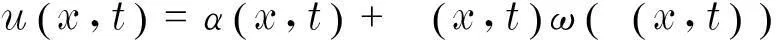
(4)

以耦合非线性Harry-Dym 方程为例,将CK直接法的步骤归纳如下：

a. 设方程(1)具有对称变换

(5)

式中,α1,α2,β1,β2,ξ是关于x,t的待定函数且G,Q是关于ξ的偏微分方程;

b. 将对称变换方程(5)代入方程(1),整理化简找出规范系数，通常以最高阶导数的系数作为规范系数;

c. 令各项导数的系数与规范系数分别成比例,应用相应规则求出待定函数;

d. 根据步骤c求出的各个变量得到对称变换,代入原方程(1),确定约化方程.

在步骤c中,提到的相应的规则为:

规则1若α1(x,t)满足形式α1=α10(x,t)+β1(x,t)Ω(ξ(x,t)),则可取Ω(ξ(x,t))=0.

规则2若α2(x,t)满足形式α2=α20(x,t)+β2(x,t)Ω(ξ(x,t)),则可取Ω(ξ(x,t))=0.

规则5如果ξ(x,t)由Ω(ξ)=ξ0(x,t)定义得出,其中,Ω(ξ)是任意可逆函数,则可取Ω(ξ)=ξ0.

3非线性耦合Harry-Dym方程的相似约化

将方程(5)代入方程(1)中,得到

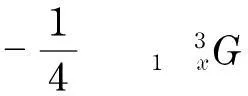
(6)

(7)

要求方程(6)和方程(7)仅仅是有关G,Q以及它们各阶导数的常微分方程.在方程(6)中用G‴的系数作为归一化系数,能够得到

式中,Γ1,Γ2,…,Γ8都是仅仅与ξ有关的待定函数.

在方程(7)中选择Q′G作为归一化系数,可得

式中,Ω1,Ω2,…,Ω7都是仅仅与ξ有关的待定函数.

现考虑ξx的两种情况.

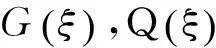
b. 当ξx≠0时,在方程(6)中由G‴和G′G前面的系数可得

(8)

对方程(8)利用上述规则3,可知

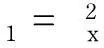
得到

利用上述规则5,可知

因此

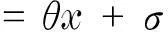
(9)

很显然

(10)

将β1=θ2,ξ=θx+σ代入方程

并利用上述规则4,可得

(11)

继续利用上述规则1和规则2,很容易得到

(12)

将式(9)～(12)代入方程

可得

(13)

因为,ξ=θx+σ,方程(13)左边是关于x的线性函数,因此,Γ3具有如下形式:

因此,有

通过比较有关x的系数,可知

(14)

(15)

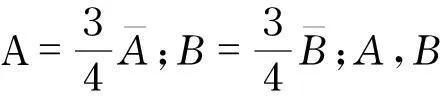
因此,非线性耦合Harry-Dym方程的对称约化为

(16)

将方程(14)～(16)代入方程(1)中,可得

(17)

考虑方程(17)的不同常数选取.

a. 当A=0时,有

式中,c1,c2是任意常数.

与之对应的对称约化为

对应方程(1)的约化方程为

(18)

b. 当A≠0时,方程(14)和方程(15)的解为

式中,c1,c2是任意常数.

与之对应的对称约化为

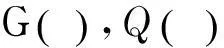
不同的约化方程(17)和方程(18),它们的通解形式只能用复杂隐函数形式来表示,这里省略其具体表达式.

4结论

利用CK直接法求得非线性耦合Harry-Dym方程的对称约化,得到了非线性耦合Harry-Dym方程的约化后的常微分方程组,进而建立了非线性耦合Harry-Dym方程与这些常微分方程组的关系.非线性耦合Harry-Dym方程的其他可积性质,如Painlevé可积性、共性Tanh可积性等[18-19],将是今后研究工作的一个重要内容.

参考文献:

[1]谷超豪.孤立子理论与应用[M].杭州:浙江科学技术出版社,1990.

[2]李翊神.孤子与可积系统[M].上海:上海科技教育出版社,1999.

[3]Xu T X,Mu W H.Finite-dimensional completely integrable systems associated with the Harry-Dym and the coupled Harry-Dym hierarchies[J].Physics Letters A,1990,147(2/3):125-129.

[4]曹策问,耿献国.系统与耦合Harry-Dym方程解的对合表示[J].数学学报,1992,35(3):314-322.

[5]Chen J B,Geng X G.A new Neumann type integrable system related to the coupled Harry-Dym hierarchy[J].Physics Letters A,2005,340(1/2/3/4):181-187.

[6]Chen J B,Geng X G.On the linearization of the coupled Harry-Dym soliton hierarchy[J].Chinese Physics B,2006,15(7):1407-1413.

[7]Yang H W,Dong H H.Multi-component Harry-Dym hierarchy and its integrable couplings as well as their Hamiltonian structures[J].Chinese Physics B,2009,18(3):845-849.

[8]Marciniak K,Blaszak M.Construction of coupled Harry-Dym hierarchy and its solutions from Stäckel systems[J].Nonlinear Analysis:Theory,Methods & Applications,2010,73(9):3004-3017.

[9]张颖,李吉娜,张江红.耦合的Harry-Dym方程的对称约化[J].西北大学学报,2011,41(6):960-963.

[10]Lie S.Uber die integration durch bestimmte integrale von einer classe linearer partieller differential-gleichungen[J].Archive for Mathematics,1881,6(3):328-368.

[11]Bluman G W,Kumei S.Symmetries and differential equations[M].New York:Springer-Verlag,1989.

[12]Olver P J.Applications of lie groups to differential equations[M].2nd ed.New York:Springer-Verlag,1993.

[13]Clarkson P A,Kruskal M D.New similarity reductions of the Boussinesq equation[J].Journal of Mathematical Physics,1989,30(10):2201-2213.

[14]Lou S Y,A note on the new similarity reductions of the Boussinesq equation[J].Physics Letters A,1990,151(3/4):133-135.

[15]Clarkson P A,Winternitz P.Nonclassical symmetry reductions for the Kadomtsev-Petviashvili equation[J].Physica D:Nonlinear Phenomena,1991,49(3):257-272.

[16]Lou S Y.Generalized Boussinesq equation and KdV equation-Painlevé properties,Bäcklund transformations and Lax pairs[J].Science in China Series A:Mathematics,1991,34(9):1098-1108.

[17]Lou S Y,Tang X Y,Lin J.Similarity and conditional similarity reductions of a (2+1)-dimensional KdV equation via a direct method[J].Journal of Mathematical Physics,2000,41(12):8286-9303.

[18]裴胜兵,张卫国,李想.色散项系数为负的mKdV-Burgers方程的有界行波解[J].上海理工大学学报,2014,36(3):205-216.

[19]刘磊,胡恒春,高海潮.Jaulent-Miodek方程的Painlevé可积性及精确解[J]. 上海理工大学学报,2014,36(3):217-222.

(编辑:石瑛)

Symmetry Reduction for the Nonlinear Coupled Harry-Dym Equation

HU Xiao,HU Hengchun

(College of Science,University of Shanghai for Science and Technology,Shanghai 200093,China)

Abstract:With the help of symbolic computation software Maple,the Clarkson-Kruskal direct method was developed for the nonlinear coupled Harry-Dym equation,the similarity variables and similarity solutions of the nonlinear coupled Harry-Dym equation were obtained by the symmetry transformation.Two forms of symmetric reduced equation were obtained by selecting different special contants.The exact solutions of the reduction equation were also constructed directly.

Keywords:symmetry reduction; Clarkson-Kruskal direct method; nonlinear coupled Harry-Dym equation

中图分类号:O 175

文献标志码:A

通信作者:胡恒春(1976-),女,副教授.研究方向:孤立子理论与可积系统.E-mail:hhengchun@163.com

基金项目:上海市自然科学基金资助项目(10ZR1420800);上海市重点学科建设项目(XTKX2012);国家自然科学基金资助项目(11071164,11201302)

收稿日期:2014-10-24

DOI:10.13255/j.cnki.jusst.2016.01.002

文章编号:1007-6735(2016)01-0008-05

第一作者: 胡潇(1991-),女,硕士研究生.研究方向:孤立子理论与可积系统.E-mail:huxiaomath@163.com