多特征融合的非刚性三维模型匹配算法研究

赖　龙,　李海生,　蔡　强,　毛典辉,　曹　健

(1.北京工商大学 计算机与信息工程学院,北京　100048;

2.北京工商大学 食品安全大数据技术北京市重点实验室,北京　100048)



多特征融合的非刚性三维模型匹配算法研究

赖龙1,2,李海生1,2,蔡强1,2,毛典辉1,2,曹健1,2

(1.北京工商大学 计算机与信息工程学院,北京100048;

2.北京工商大学 食品安全大数据技术北京市重点实验室,北京100048)

摘要：特征描述符是影响非刚性三维模型匹配结果的关键因素,而单一特征只能描述三维模型某一方面的信息.为了克服单一特征在模型匹配时的局限性,进一步提高模型匹配的精确度,通过引入信息论中信息熵的概念,结合各单一特征匹配时的结果,计算得到各特征的权值,对多种特征(如热核特征(HKS)、能量分布特征(WKS)和模型表面积特征等)进行融合,作为非刚性三维模型匹配的特征.最后在SHREC’2014提供的标准测试数据集上进行试验,并与单一特征描述符的结果进行对比,验证了多特征融合得到的特征描述符要优于任一单一特征描述符,可以应用于非刚性三维模型检索系统中.

关键词：非刚性; 信息熵; 多特征

三维模型是指在计算机中存储的具有三维几何信息的模型数据,一般用网格或点云进行表示.随着各种三维建模软件的广泛使用,三维模型的数量呈指数级增长,获取三维模型的方式也越来越多.如何提高现有的三维模型的复用率,帮助设计者在海量的三维模型中找到需要的三维模型,是一项非常有挑战的任务.目前比较著名的三维模型检索系统有美国普林斯顿大学的形状检索与分析实验室研发的3D Model Search Engine,中国台湾大学实现的基于光场描述符的3D Model检索系统等.

三维模型主要分为刚性三维模型和非刚性三维模型.在理论上,若模型在发生形变时保持等距不变性、拉伸不变性、关节变形不变性、拓扑不变性等(如人手模型姿态的变化[1]),该模型可被视为非刚性三维模型.常见的检索系统大多针对刚性三维模型,刚性三维模型的处理分析方法更多关注平移、旋转及缩放的不变性[2-3],不适用于非刚性的模型.目前已经有一些学者提出了处理非刚性三维模型的方法,常见的有谱分解方法[4-5]和基于几何特征的方法[6]等.其中,热核特征(heat kernel signature,HKS)[7]和能量分布特征(wave kernel signature,WKS)[8]是谱分解方法中效果较好的特征.测地距离[9-10]和模型表面积属于模型几何特征[6],但是每种特征都存在一定的缺点,如HKS只能保留模型低频部分的信息,而导致模型高频部分信息的缺失.WKS和模型表面积特征侧重于模型宏观上的整体信息;同时,在谱分解方法中,当得到的特征值非常接近时,各特征值对应的特征向量会对最终的特征描述符造成一定的影响.

传统的单一特征描述符难以全面描述模型信息,Ortega等[11]证明对多种单一特征,通过加权融合后再进行检索可以得到更好的结果.国内已有学者尝试使用多特征融合去提高三维模型检索的效率[12],但是他们的算法中特征融合的权值是基于用户反馈的,算法流程相对复杂.本文提出的多特征融合的非刚性三维模型匹配算法,根据单一特征匹配的结果以及已知的分类信息分别计算每种算法的熵值,根据熵值得到该算法对应的权值.最后在单一特征匹配结果的基础上,得到最终的多特征融合的匹配结果.

1非刚性三维模型特征提取方法

通过综合分析各种非刚性三维模型特征的特点,本文将对HKS,WKS和模型表面积特征进行融合.

1.1HKS特征提取

热核特征反映了热量在模型表面传递的过程,通过对不同时刻下,模型表面的热量分布状况来描述模型的表面及特征.热核具有等距等容不变性的特点,非常适合作为非刚性三维模型的特征描述符.对于一般的黎曼流形,构造其Laplace-Beltrami算子是求得模型热核的关键.在图形图像领域,通常用余切法去构造Laplace-Beltrami算子.本文将采用Belkin等[13]提出的一种对余切法的改进方法去近似表示该算子,这种方法可以克服原始的余切法在一般情况下不收敛的缺点.

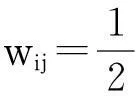
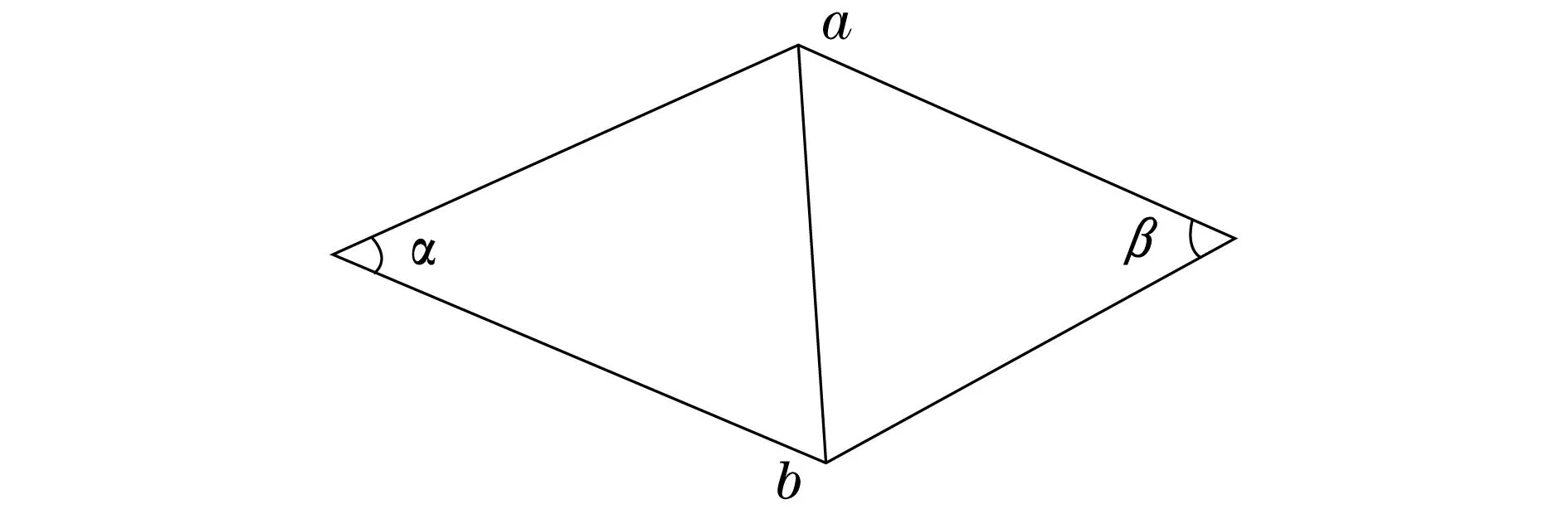
图1　xi和xj之间的权值的确定

基于Laplace-Beltrami算子的特性,Sun等[7]提出了HKS特征的定义.对于模型上的任一点x在t时刻的HKS被定义为

(1)

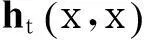
1.2WKS特征提取

WKS特征反映了模型上各顶点在被作为不同能量等级的量子粒子情况下的概率分布.由于粒子的能量与其频率有关,WKS可以被视为是在一定时间条件下,模型上各点的频率信息.模型表面各顶点关于时间的能量函数是Schrödinger方程的解,如式(2)所示.

(2)

与HKS特征提取类似,根据模型的顶点信息使用改进的余切法构造其Laplace-Beltrami算子L.对L进行特征分解,并只保留其最小的100～300个特征值及其对应的特征向量.与HKS特征提取不同的是,对于t=0的时刻,模型将被设置一个初始能量E.根据一定规则,可以得到一个基于模型顶点能量的期望为E的概率分布.假设L的特征值不重复,能量函数可以表示为

(3)

WKS作为平均的概率值,被定义为

(4)

由于eiEkt是正交的,WKS可以进一步改写为

(5)

从式(5)中可以看到,与HKS相比,这里不再有时间参数,而有一个与初始能量E有关的函数,初始能量E又与L的特征值有关,这样便避免了人为设置的时间t对模型特征的影响.

根据上面对于WKS的理论分析,在实际的实验中,模型上各点的WKS值被定义为

(6)

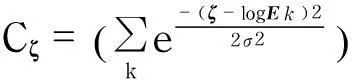
WKS(x,ζ)便是该模型的各点对应的WKS特征.

1.3模型表面积特征提取

在各种基于几何特征的方法中,基于模型表面积的特征提取是简单高效的特征提取算法之一.模型表面积特征就是直接计算模型的表面积作为该模型的特征.这种方法虽然对模型的尺度敏感,且会忽略模型的局部细节,但便于计算,对于存在非刚性形变的三维模型有很好的效果.Pickup等[6]的实验结果表明,这种算法的效果在一定程度上比某些复杂的算法(如HKS特征提取)更优秀.

2非刚性三维模型多特征融合匹配算法实现

2.1基于信息熵的多特征权值分配

为了弥补单一特征在描述三维模型时的局限性,本文引入了多特征融合的方法.通过多个特征进行融合可以更加全面地描述模型,根据所处理的模型库的特点,实现各个特征之间的取长补短,使各特征的优势最大化.

由于各种特征描述符对模型的描述能力不同,在进行特征融合时,特征的权值是关键参数.最简单的处理方式是给各种特征赋相同的权值,但这种权值设定下进行的实验结果很不理想.为了优化权值分配,本文将信息论中信息熵的思想引入进来,通过计算每种特征的信息熵去进一步确定该特征对应的权值.

对于有n个模型的数据集D,将f1,f2和f3这3种算法进行融合,其权值分配方法如下:

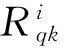
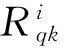
(7)

(8)

c. 根据信息熵的定义,特征fi对应的信息熵可表示为

(9)

进而,计算出各特征的权值为

(10)

F1,F2和F3分别是f1,f2和f3的权值.

2.2多特征融合匹配算法实现流程

在得到各特征对应的权值之后,可以对f1,f2和f3这3种算法进行融合,提高匹配的精确度,其流程如下:

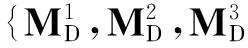
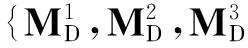
(11)

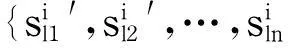
c. 模型l与其余模型在不同特征条件下计算的相似度进行融合,如计算模型l与模型j在多特征融合后的相似度为

(12)

Sim是最终的相似度.通过该相似度,可以组成相似度矩阵,其中记录了所处理的数据集中任两个模型之间的相似度,对该矩阵中内容进行评估可以量化当前匹配算法的优劣.

3实验

3.1实验数据集

三维模型检索竞赛(3D SHape REtrieval Contest,简称SHREC)[14]是Eurographics举办的每年一届的三维模型检索大赛,几乎每届SHREC竞赛都会提出新的非刚性三维模型的数据集,本文采用SHREC’2014提供的非刚性三维模型数据集[6]进行试验.SHREC’2014非刚性三维模型的数据集共有两个子集,Real数据集和Synthetic数据集.Real数据集中的模型是直接扫描真实的人体构建的,该数据集共包含400个姿态各异的模型.其中,每个模型的顶点数范围为14 996～15 000,面片数范围为29 968～29 996.Synthetic数据集中的模型则是用三维模型建模软件生成的,该数据集的模型数量为300个,其中每个模型的顶点数范围为60 086～60 277,面片数范围为120 080～120 451.图2是SHREC’2014提供的2个非刚性数据集示例.

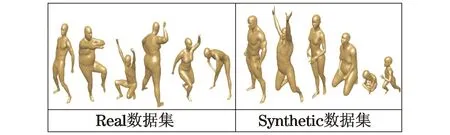
图2　SHREC’2014非刚性三维模型数据集示例

3.2性能评估标准

评估标准为国际上通用的由普林斯顿大学提出的评估标准[15],该标准主要评估基于某种特征的相似度矩阵,包括最近邻方法(nearest neighbor,简称NN)、 第一层级(first-tier,简称1-T)和第二层级(second-tier,简称2-T)、E-度量(E-Measure,简称2-M )、折扣的累积结果(discounted cumulative gain,简称DCG).

a. 最近邻方法:表示与待查询模型同属于一类的模型所占返回的检索结果的比例,比例越低,则说明检索出的相似结果越少.

b. 第一层级和第二层级:对于返回结果保存最相似的前K个模型 (K的大小与待查询模型所在类的规模有关),第一层级和第二层级表示出现在前K个模型中,与输入模型属于同一类的模型所占的比例,该比例越低,说明检索出的相似结果越少.对于待查询模型的类别,可定义该类别包含模型数G,则对于第一层级来说,K=G,对于第二层级,K=2G.

c. E-度量:是一种改进的Precision- Recall评价标准.对于检索结果,用户更感兴趣的应该是前面页面的检索结果而不是后面页面的检索结果,因此E-Measure只考虑前32个检索结果并计算Precision-Recall.其最大值为1.0,数值越大则检索结果越好.

d. 折扣的累积结果:加权的正确结果的列表,其中越靠前权重越大.

3.3实验流程

本文实验是在内存为2 GB,CPU为Intel 2.6 GHz双核的PC机和Windows 8环境下完成的.

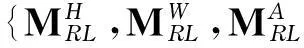
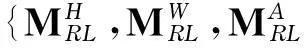
3.4实验结果及分析

实验对比结果如表1和表2所示.

表1　Real数据集实验结果性能评估

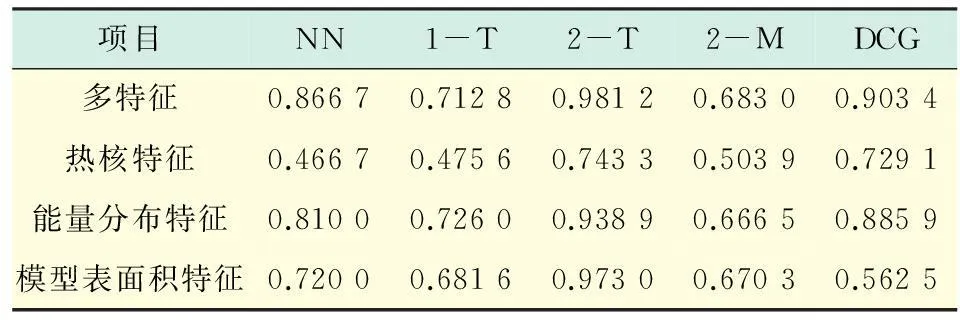
表2　Synthetic数据集实验结果性能评估

同时,本文也将几种单一特征描述符与多特征描述符的结果进行了可视化对比,如图3所示.纵坐标表示各特征描述符采用5种不同的评估标准进行评估时所对应的结果,最大值为1.

从图3中的直方图可以明显看到,无论是针对Real数据集还是Synthetic数据集,在单一特征的条件下,使用WKS特征和Surface特征的评估得分更高.而多特征融合的表现要明显优于单特征,在对Real数据集进行处理时,多特征融合比效果最好的单一特征(WKS)提高了10%.对于在单特征条件下评分已经很高的Synthetic数据集,多特征融合的评分依然高于任一单特征.

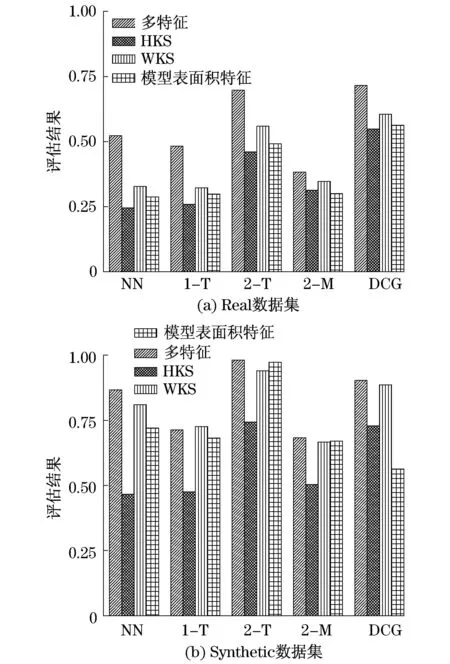
图3　算法评估结果对比图

为了直观地观察多特征融合之后的效果,本文分别随机选取了Real数据集和Synthetic数据集中的一个模型作为输入,计算它们与相应数据集中的其余模型之间的相似度,对最相似的10个模型进行可视化输出,位置越靠左表示相似程度越高，结果如图4所示(见下页).模型①为Real数据集中的模型,模型②为Synthetic数据集中的模型,虚线框标示的是错误的检索结果.从图4中的两组结果可以看到,本文实验中所实现的4种方法,使用了多特征融合的检索效果最好.

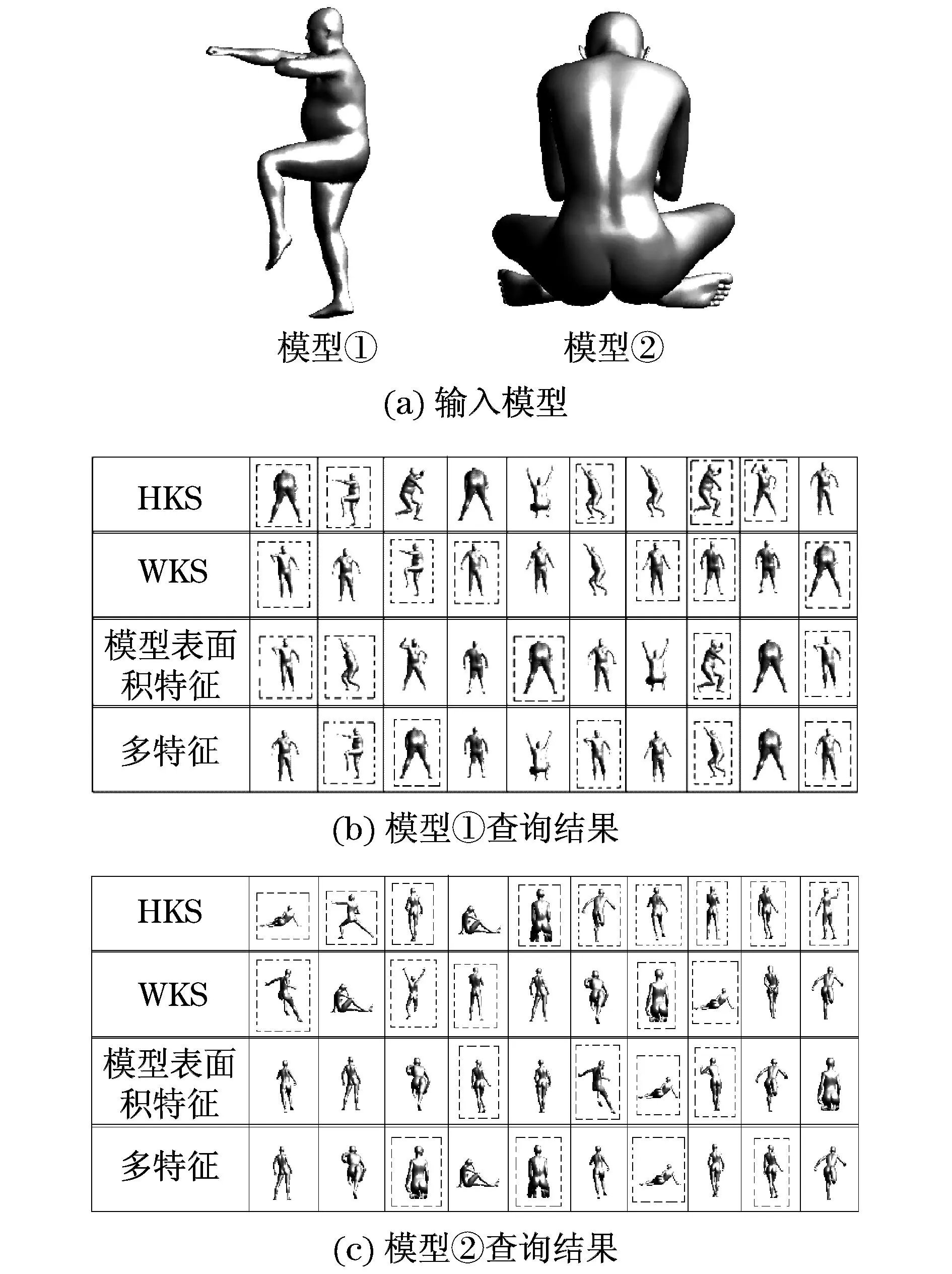
图4　输入模型查询示例

4结论与展望

HKS,WKS等谱分解方法提取的特征是当前针对非刚性三维模型的一类优秀的特征.但是单一特征有一定的局限性,恰当地融合不同的形状特征可使它们优势互补,更好地描述非刚性三维模型.本文提出了一种多特征融合的非刚性三维模型匹配算法,先计算待融合特征的信息熵,将该信息熵转化成权值,对单一特征下的模型间相似度进行加权融合,得到的相似度作为新的模型间相似度.通过使用普林斯顿大学的评估标准进行评估以及进行了模拟三维模型检索的可视化展示可以看到,使用多特征融合可以在一定程度上提高模型匹配的效果.

在以后工作中,将继续探索新的非刚性三维模型的特征描述符,并尝试将本文中算法引入到实际的应用中.

参考文献：

[1]刘敏娟,崔建昆.手指可达工作空间的三维建模[J].上海理工大学学报,2006,28(1):95-98.

[2]Li B,Lu Y J,Godil A,et al.A comparison of methods for sketch-based 3D shape retrieval[J].Computer Vision and Image Understanding,2014,119:57-80.

[3]Yang Y B,Lin H,Zhang Y.Content-based 3D model retrieval:a survey[J].IEEE Transactions on Systems,Man,and Cybernetics,Part C:Applications and Reviews,2007,37(6):1081-1098.

[4]Li C Y,Hamza A B.Spatially aggregating spectral descriptors for nonrigid 3D shape retrieval:a comparative survey[J].Multimedia Systems,2014,20(3):253-281.

[5]Litman R,Bronstein A M.Learning spectral descriptors for deformable shape correspondence[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2014,36(1):171-180.

[6]Pickup D,Sun X F,Rosin P L,et al.SHREC’14 track:shape retrieval of non-rigid 3D human models[C]∥Eurographics Workshop on 3D Object Retrieval.Strasbourg:The Eurographics Association,2014:101-110.

[7]Sun J,Ovsjanikov M,Guibas L.A concise and provably informative multi-scale signature based on heat diffusion[J].Computer Graphics Forum,2009,28(5):1383-1392.

[8]Aubry M,Schlickewei U,Cremers D.The wave kernel signature:a quantum mechanical approach to shape analysis[C]∥Proceedings of IEEE International Conference on Computer Vision Workshops (ICCV Workshops).Barcelona:IEEE,2011:1626-1633.

[9]Xin S Q,Wang G J.Improving Chen and Han’s algorithm on the discrete geodesic problem[J].ACM Transactions on Graphics (TOG),2009,28(4):104.

[10]Raviv D,Bronstein A M,Bronstein M M,et al.Affine-invariant geodesic geometry of deformable 3D shapes[J].Computers & Graphics,2011,35(3):692-697.

[11]Ortega M,Rui Y,Chakrabarti K,et al.Supporting similarity queries in MARS[C]∥Proceedings of the Fifth ACM International Conference on Multimedia.New York:ACM,1997:403-413.

[12]杨萌.基于多特征和相关反馈的三维模型检索系统研究与实现[D].西安:西北大学,2009.

[13]Belkin M,Sun J,Wang Y S.Discrete Laplace operator on meshed surfaces[C]∥Proceedings of the Twenty-Fourth Annual Symposium on Computational Geometry.New York:ACM,2008:278-287.

[14]Vandeborre J P,Tabia H.The seventh Eurographics workshop on 3D object retrieval[DB/OL].[2014-04-06].http:∥3dor2014.ensea.fr/People.html.

[15]Shilane P,Min P,Kazhdan M,et al.The princeton shape benchmark[C]∥ Proceedings of Shape Modeling Applications.New York:IEEE,2004:167-178.

(编辑:丁红艺)

Non-rigid 3D Models Matching with Multi-feature Fusion

LAI Long1,2,LI Haisheng1,2,CAI Qiang1,2,MAO Dianhui1,2,CAO Jian1,2

(1.School of Computer and Information Engineering,Beijing Technology and Business University,Beijing 100048,China;2.Beijing Key Laboratory of Big Data Technology for Food Safety,Beijing 100048,China)

Abstract：Feature descriptors are the key factors influencing the result of non-rigid 3D model correspondence.But a single feature descriptor only contains one aspect of information of a 3D model.In order to overcome the limitation of single feature and further improve the accuracy of model correspondence,the entropy was introduced to calculate the weight of each single feature according to its correspondence results.The features of HKS(heat kernel signature),WKS(wave kernel signature) and surface area were fused with these weights.The effectiveness of the approach was evaluated by using the SHREC’2014 non-rigid 3D human models benchmark.In addition,the results outperform those of any state-of-the-art single feature descriptor,and can be used for non-rigid 3D model retrieval.

Keywords：non-rigid; entropy; multi-feature

中图分类号：TP 391

文献标志码：A

通信作者：李海生(1974-),男,教授.研究方向:计算机图形学、科学可视化等.E-mail:lihsh@th.btbu.edu.cn

基金项目：国家重点实验室开放基金资助项目(BUAA-VR-14KF-04);北京市自然科学基金资助项目(4162019);北京市重点实验室专项基金资助项目(19008001069);北京市教委科研计划一般项目(201610011010)

收稿日期：2014-12-23

DOI：10.13255/j.cnki.jusst.2016.01.014

文章编号：1007-6735(2016)01-0081-06

第一作者： 赖龙(1988-),男,硕士研究生.研究方向:三维模型检索.E-mail:lailong@163.com