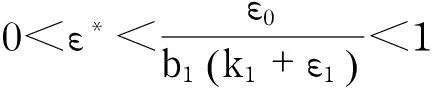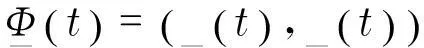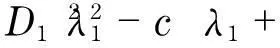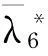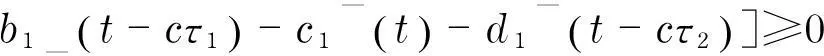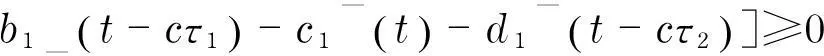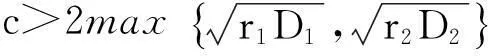一类具有时滞的反应扩散Lotka-Volterra竞争系统行波解的存在性

徐　芳,　张卫国,　余志先

(上海理工大学 理学院,上海　200093)



一类具有时滞的反应扩散Lotka-Volterra竞争系统行波解的存在性

徐芳,张卫国,余志先

(上海理工大学 理学院,上海200093)

摘要：研究了一类具有时滞的Lotka-Volterra竞争系统行波解的存在性.应用具有时滞的反应扩散系统行波解存在性理论,将所研究系统行波解存在性的问题转化为寻找该系统的一对上、下解.给出了该系统在无穷远处的渐进衰减行为,完善并改进了同类系统行波解存在性的结论.

关键词：时滞; Lotka-Volterra竞争系统; 行波解; 存在性; 上下解

1问题的提出

反应扩散方程在描述时空模式方面起着很重要的作用,其行波解可以用来解释自然界中的有限速度传播现象、有限震动现象等,从而备受关注[1-16].行波解的概念是1937年Kolmogorov在文献[1]中提出的,用来解释一维无穷动物栖息地上优良基因的传播过程.而具有空间扩散项的两个种群的Lotka-Volterra竞争系统是生物数学研究领域中比较典型且比较重要的模型之一,其模型为

(1)

许多学者对系统(1)的行波解作了广泛的研究[2-8],文献[2,5,8]分别利用相平面分析法、指数同伦法、度理论的技巧得到了系统(1)的行波解的存在性.

物种的繁殖由于受到妊娠、环境及成熟过程等各方面因素的影响,物种密度在时间上的滞后是在所难免的,所以,具有时滞的Lotka-Volterra竞争系统得到了学者们的关注.

(2)

式中,τ1,τ2,τ3,τ4表示反馈时滞.

但是,先前的一些方法不能够运用到类似系统(2)这样具有时滞的反应扩散Lotka-Volterra竞争系统中去.于是,Lü等[9]利用单调迭代方法和上下解的技巧研究了系统(2)的行波解;Li等[10]利用Shauder不动点定理和新的交叉迭代的方法得出了系统(2)的行波解的存在性.

在自然界中,两个物种的种群数量受到各自的固有增长率的影响,与此同时,在时间t,t-τi(i=1,2,3,4)自身的以及竞争物种的种群密度增加时,两个物种的种群密度增长率都会下降,这表明两个竞争物种的种群密度均分别受到自身在时间t,t-τi(i=1,3)以及竞争物种在时间t,t-τi(i=2,4)时种群密度的影响.受到学者们对式(1)和式(2)的研究的引导,以及文献[10-11]的结论的启发,本文研究以下的Lotka-Volterra竞争系统：

(3)

式中:a1,b1,a2,b2表示物种内部的拥挤系数;c1,d1,c2,d2表示两个物种之间的竞争系数.

综合考虑现实物种的生长受到多方面内部及外部因素的影响,系统(3)这个模型具有更强的现实生物意义.

2预备知识

具有时滞的反应扩散系统的一般形式为

(4)

式中:D1,D2>0;fi:2→,i=1,2,且fi是连续函数.

系统(4)的行波解是一对形如u1(x,t)=φ(x+ct),u2(x,t)=ψ(x+ct)的特解,其中,(φ,ψ)∈C2(,2),c>0,c是波速.将u1(x,t)=φ(x+ct),u2(x,t)=ψ(x+ct)代入系统(4)且仍然用t来代替x+ct,则系统(4)的行波解满足下面的泛函微分方程:

(5)

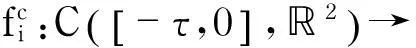
(6)

的解.

现给出一些假设:

A2存在2个常数L1,L2>0,使得

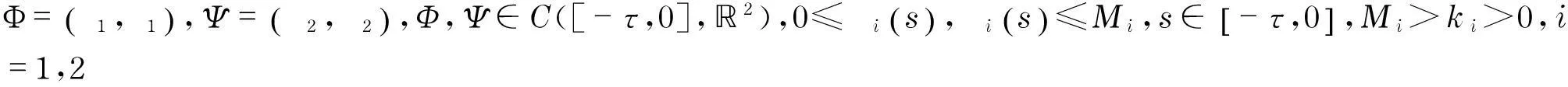
A3(文献[10,12]中的WQM*条件),存在β1,β2>0,使得

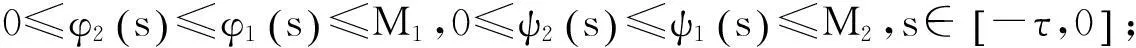
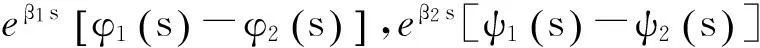
定义集合

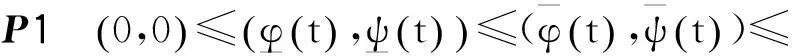
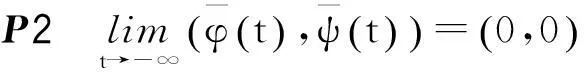
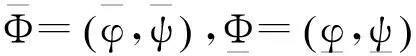
(7)

(8)

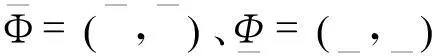
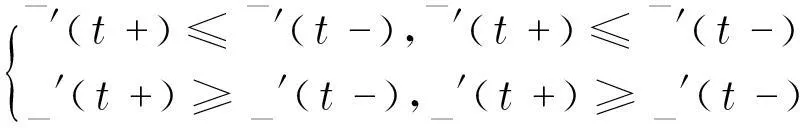
(9)

文献[13-14]进一步将具有时滞的反应扩散系统(4)的行波解的存在性推广到具有时滞的n个方程组和时空时滞的方程组的行波解的存在性.

3系统(3)的行波解的存在性

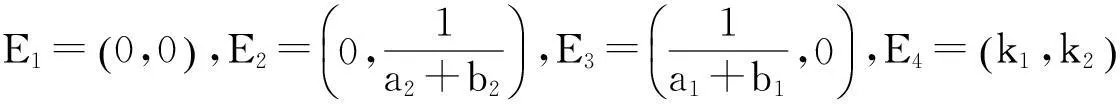
将u1(x,t)=φ(x+ct),u2(x,t)=ψ(x+ct)代入系统(3)且仍然用t来代替x+ct,得

(10)

本文将研究系统(3)连接平衡点E1,E4的行波解的存在性,即研究系统(10)满足边值条件

(11)

的解的存在性.

对φ,ψ∈([-τ,0],),其中,τ=max{τ1,τ2,τ3,τ4},记

(12)

易得f1,f2满足假设A1和A2.

3.1系统(10)满足WQM*条件

证明令Φ(s)=(φ1(s),φ2(s)),Ψ(s)=(ψ1(s),ψ2(s)),Φ(s),Ψ(s)∈C([-τ,0],2),且

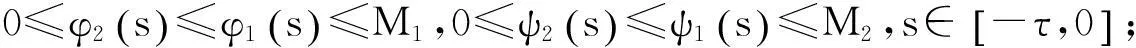
b.eβ1s[φ1(s)-φ2(s)]，eβ2s[ψ1(s)-ψ2(s)]不减,s∈[-τ,0].

于是

f1(φ1,ψ1)-f1(φ2,ψ1)=r1φ1(0)[1-

a1φ1(0)-b1φ1(-τ1)-c1ψ1(0)-

d1ψ1(-τ2)]-r1φ2(0)[1-a1φ2(0)-

b1φ2(-τ1)-c1ψ1(0)-d1ψ1(-τ2)]=

r1[φ1(0)-φ2(0)]-r1d1ψ1(-τ2)·

r1b1[φ1(0)φ1(-τ1)-φ2(0)φ2(-τ1)]-

r1c1ψ1(0)[φ1(0)-φ2(0)]≥(r1-

r1d1M2-2r1a1M1-r1c1M2)[φ1(0)-

φ2(0)]-r1b1φ2(0)[φ1(-τ1)-

φ2(-τ1)]-r1b1φ1(-τ1)[φ1(0)-φ2(0)]≥

r1(1-2a1M1-b1M1-c1M2-d1M2)·

[φ1(-τ1)-φ2(-τ1)]≥r1(1-2a1M1-

b1M1-c1M2-d1M2-b1M1·

eβ1τ1)[φ1(0)-φ2(0)]

当τ1>0且充分小,则存在β1>0,使得

因此

同理可得,当τ3>0且充分小,则存在β2>0,使得

另外

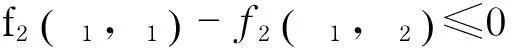
引理1得证.

3.2系统(10)的一对弱上、下解

又因为a1+b1>c2+d2,a2+b2>c1+d1,则存在ε0,ε1,ε3>0,使得

(13)

对以上的常数以及适当的常数t2,t4>0,定义以下连续函数:

(14)

(15)

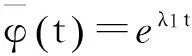
b. 当t≥t2+cτ1时,有t-cτ2≥t3,

r1(k1+ε1e-λt)[1-a1(k1+ε1e-λt)-

b1(k1+ε1e-λ(t-cτ1))-c1(k2-ε4e-λt)-

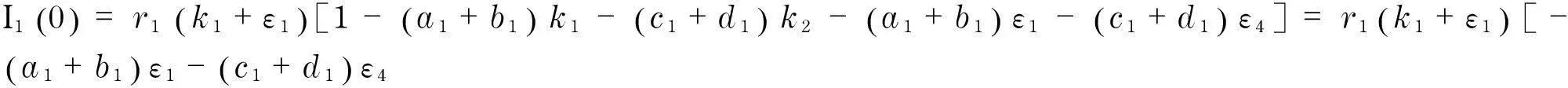
c. 当t2

于是

类似地,对任意的t∈,存在>0,使得对时,有

a. 当t≤t1时,有t≤t4,

因此

b1(eλ1(t-cτ1)-qeηλ1(t-cτ1))+c1eλ3t+d1eλ3(t-cτ2)]=

cηλ1+r1)-r1(eλ1t-qeηλ1t)[a1(eλ1t-

qeηλ1t)+b1(eλ1(t-cτ1)-qeηλ1(t-cτ1))+c1eλ3t+

r1eλ1t[a1eλ1t+b1eλ1(t-cτ1)+c1eλ3t+

r1eλ1t[(a1+b1)eλ1t+(c1+d1)eλ3t]=

b. 当t≥t1+cτ1时,

且对任意的t∈,有.于是,

从而

c. 当t1

对任意的t∈,有.则

同理可证,对任意的t∈,存在>0,使得对有

引理2得证.

结合定理1、引理1和引理2，可得定理2.

参考文献：

[1]Kolmogorov A N.A study of the equation of diffusion with increase in the quantity of matter,and its application to a biological problem[J].Moscow University Bulletin of Mathematics,1937(1):1-25.

[2]Van Vuuren J H.The existence of traveling plane waves in a general class of competition-diffusion systems [J].IMA Journal of Applied Mathematics,1995,55(2):135-148.

[3]Tang M M,File P C.Propagating fronts for competing species equations with diffusion[J].Archive for Rational Mechanics and Analysis,1980,73(1):69-77.

[4]Gourley S A,Ruan S.Convergence and travelling fronts in functional differential equations with nonlocal terms:a competition model [J].Siam Journal on Mathematical Analysis,2003,35(3):806-822.

[5]Conley C,Gardner R.An application of the generalized Morse index to travelling wave solutions of a competitive reaction-diffusion model[J].Indiana University mathematics Journal,1984,33(3):319-343.

[6]Gardner R A.Existence and stability of travelling wave solutions of competition models:a degree theoretic approach[J].Journal of Differential Equations,1982,44(3):343-364.

[7]Kanon Y.Parameter dependence of propagation speed of travelling waves for competition-diffusion equations[J].Siam Journal on Mathematical Analysis,1995,26(2):340-363.

[8]Kanel J,I,Zhou L.Existence of wave front solutions and estimates of wave speed for a competition-diffusion system[J].Nonlinear Analysis:Theory,Methods & Applications,1996,27(5):579-587.

[9]Lü G Y,Wang M X.Traveling wave front in diffusive and competitive Lotka-Volterra system with delays[J].Nonlinear Analysis:Real World Applications,2010,11(3):1323-1329.

[10]Li W T,Lin G,Ruan S G.Existence of traveling wave solutions in delayed reaction-diffusion systems with applications to diffusion-competition systems[J].Nonlinearity,2006,19(6):1253-1273.

[11]Xia J,Yu Z X,Traveling wave solutions in temporally discrete reaction-diffusion systems with delays [J].Zamm-Journal of Applied Mathematics and Mechanics,2011,91(10):809-823.

[12]Yu Z X,Yuan R.Traveling waves for a Lotka-Volterra competition system with diffusion [J].Mathematical and Computer Modelling,2011,53(5/6):1035-1043.

[13]Yu Z X,Yuan R.Traveling waves of delayed reaction diffusion systems with applications [J].Nonlinear Analysis Real World Applications,2011,12(5):2475-2488.

[14]Yu Z X,Zhao H K.Traveling waves for competitive Lotka-Volterra systems with spatial diffusions and spatio-temporal delays [J].Applied Mathematics and Computation,2014,242:669-678.

[15]刘艺昕,余志先.格上时滞单种群模型的行波解的渐近性[J].上海理工大学学报,2015,37(4):322-326.

[16]夏静,余志先,袁荣.一类具有非局部扩散的时滞Lotka -Volterra竞争模型的行波解[J].应用数学学报,2011,34(6):1082-1093.

(编辑:石瑛)

Existence of Traveling Wave Solutions for Reaction-Diffusion Lotka-Volterra Competitive System with Delays

XU Fang,ZHANG Weiguo,YU Zhixian

(College of Science,University of Shanghai for Science and Technology,Shanghai 200093,China)

Abstract：The existence of traveling wave solutions for two species Lotka-Volterra competitive system with delays was investigated.Based on the theory of the existence of traveling wave solutions for reaction-diffusion systems with delays,the main problem was transfered to look for a pair of upper and lower solutions for the system.And the asymptotic behavior of the system was given as an attenuated motion tending to the infinity.The study makes up and improves the results of the existence of traveling wave solutions of a class of systems.

Keywords：delay; Lotka-Volterra competitive system; traveling wave solution; existence; upper and lower solution

中图分类号：O 175.2

文献标志码：A

通信作者：张卫国(1957-),男,教授.研究方向:非线性系统的理论与应用.E-mail:zwgzwm@126.com

基金项目：国家自然科学基金资助项目(11071164,11101282,11271260);上海市教委科研创新项目(13ZZ118,14YZ096);上海市一流学科(系统科学)建设项目(XTKX2012);沪江基金资助项目(B14005)

收稿日期：2014-08-27

DOI：10.13255/j.cnki.jusst.2016.01.001

文章编号：1007-6735(2016)01-0001-07

第一作者： 徐芳(1989-),女,硕士研究生.研究方向:非线性系统的理论与应用.E-mail:sipangzixu@163.com