基于动态几何系统的初等代数表达式计算研究
陈晓霞
(1.浙江科技学院 理学院,杭州 310023;2.华中师范大学 国家数字化学习工程技术研究中心, 武汉 430079)
基于动态几何系统的初等代数表达式计算研究
陈晓霞1,2
(1.浙江科技学院 理学院,杭州 310023;2.华中师范大学 国家数字化学习工程技术研究中心, 武汉 430079)
摘要:解析平面动态几何系统中所涉及的几何图元对象的代数方程代数,将之表示为几何对象的代数属性,利用树形结构及堆栈方法对含参数的代数表达式进行解析和计算,构建具备含参数的初等代数表达式计算模块的平面动态几何系统,可以很好地将平面解析几何的内容融合进来,从而丰富了平面动态几何系统的功能,提高了平面动态几何系统的运行效率。
关键词:平面几何;动态几何;平面解析几何;代数表达式
平面欧氏几何及其代数化的平面解析几何一直以来都是中国中学数学学习的重要内容,其中二次曲线的形态与其代数方程之间的关系,直线与二次曲线间的位置关系与其方程之间的关系等内容,是中学平面几何中重要的教学内容。学生如果可以通过动态几何系统来观察、模拟、变换二次曲线及直线,从而进行直观生动的学习,就将对解析几何内容的掌握带来很大的帮助。因此,构建包含解析几何内容的平面动态几何系统将使其具备更广泛的应用。
另外,如果利用代数方法和欧氏几何的公理体系相结合的方法来构建动态几何系统,可以提高动态几何系统的运行效率,丰富动态几何系统功能,增强动态几何系统操作的便捷性和直观性。因此,在构建平面动态几何系统时,构建合适的解析几何模块是十分必要的。
自20世纪90年代起,几何画板(The Geometry’s SketchPad)[1]、超级画板(Super Smart Platform)[2]、GeoGebra[3]、Carbri Geometry[4]等动态几何系统被广泛应用于数学教学中[5-9],其中由中国著名数学家张景中院士主导开发的超级画板系统将解析几何模块很好地融入平面动态几何系统中,相较于其他动态几何系统,超级画板的作图功能更为丰富、作图效率更高[10-12]。本研究就超级画板系统中解析几何模块所涉及的代数表达式计算方法进行分析和研究。
利用堆栈或二叉树等方法可实现含参数表达式的计算,详见文献[13-16]。这些算法具有一定的普遍适用性,针对平面动态几何系统的需求,笔者对这些算法进行一定的修改,从而创建服务于平面解析几何的含参数代数表达式的计算方法。
在平面动态几何系统中创建解析几何模块,需在该系统中解决如下问题:
1)几何图元对象的代数化及标准化。
2)已知曲线方程,通过计算绘制曲线的图形。
3)可求解曲线与曲线、曲线与直线之间的交点。
4)用户输入含参数的代数表达式,可运算在一定精度范围内相应参数取值确定时该表达式的浮点型数值。
因此,含参数代数表达式计算在平面动态几何系统中应用的核心问题是,几何图元对象的代数化及含参数代数表达式的数值计算方法。
1含参数代数表达式的计算在平面动态几何系统中的应用
1.1几何图元对象的代数化
鉴于上述讨论,将代数表达式计算算法应用于平面动态几何系统,首先需要对平面动态几何系统中所涉及的几何图元对象进行代数化。几何图元对象的代数化是指使用一些用来表示几何图元的代数变量来描述几何图元对象,称这些代数变量为几何图元对象的代数属性。由于在解析几何系统中几何图元对象与其代数方程是一一对应的,因此可通过解析几何图元对象的代数方程来实现几何图元对象的代数化。为实现此代数化过程,在此平面动态几何系统中,首先需构造一个独立的直角坐标系系统,称之为逻辑直角坐标系。在此坐标系下,当用户需要构造新的几何对象时,首先根据所构造的几何图元的类型获得其父对象(即其存在的必要条件)的代数属性,并据此计算该几何图元的代数属性以备构造。
在平面动态几何系统中所涉及的几何图元对象,包括点、直线、圆(特殊的圆锥曲线)、圆锥曲线、初等函数曲线,其代数属性分别为:
1)点的代数属性,在逻辑直角坐标系系统下点的坐标x,y。
2)直线的代数属性,直线的标准方程ax+by+c=0中的系数a、b、c。
3)圆锥曲线的代数属性,圆锥曲线的标准方程ax2+bxy+cy2+dx+ey+f=0中的系数a、b、c、d、e。
4)初等函数曲线的代数属性,如果函数方程为y=f(x),则使用表示f(x)的字符串sy表示其代数属性;如果函数方程为x=f(y),则使用表示f(y)的字符串sx表示其代数属性。
以下为常见几何图元的代数属性计算方法。
1)线段代数属性的计算。线段的2个端点为待构造线段的父对象,其代数属性计算过程如下:
首先,系统获得父对象点,称为point1、point2,并获得它们的代数属性,即其坐标x1、y1和x2、y2。
2)以点斜式方程来表示的直线的代数属性的计算。待构造的直线为过定点已知斜率的直线,已知定点为该直线的父对象,其代数属性计算过程如下:
首先,系统获得待构造直线的父对象的代数属性,表示为x1、y1。
其次,要求用户通过对话框输入表示斜率的含参数代数表达式,通过下文所阐述的含参表达式计算方法算得该表达式所对应的数值,使用字母k表示该斜率。
根据直线的点斜式方程y-y1=k(x-x1),标准化方程为kx-y-kx1+y1=0,所以,该线段的代数属性a、b、c分别为表达式k、-1和k*x1+y1的值。
3)过已知点与已知直线平行的直线的代数属性的计算。已知点及已知直线为待构造直线的父对象,其代数属性计算过程如下:
系统获得父对象点和直线的代数属性,表示为x0、y0,以及a1、b1和c1,该直线的代数属性a、b即父直线的代数属性a1和b1,c为表达式-(a1*x1+b1*y1)的值。
4)已知圆心和圆上一点的圆的代数属性的计算。已知两点为待构造圆的父对象,其代数属性计算过程如下:
首先获得父对象的代数属性,表示为x1、y1、x2、y2。
其次,根据公式(x-x1)2+(y-y1)2=(x2-x1)2+(y2-y1)2标准化后的方程中各系数为圆的各代数属性,其中a=1、b=0、c=1,d、e、f分别为表达式-2*x1,-2*y1和(x1)∧2+(y1)∧2-(x2-x1)∧2-(y2-y1)∧2的值。
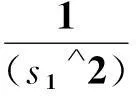
1.2含参数的初等代数表达式的数值计算
含参数的初等代数表达式的数值计算包括:表达式解析和表达式数值计算两部分。
1.2.1表达式解析过程
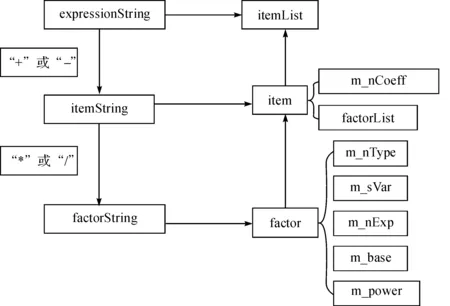
图1 表达式解析图Fig.1 Expression analysis
表达式解析过程如图1所示。
第一步,将一个表示初等运算的字符串expressionString以“+”或“-”为分隔符分隔为若干“项字符串”itemString。
第二步,将项字符串itemString以“*”或“/”分隔为若干“因子字符串”factorString。
第三步,将itemString分解为“项”item,每个item由一个系数m_nCoeff和一个“因子列表”factorList构成,如果项之间的分隔符为“-”,分隔符后的项的系数乘以-1。
第四步,每个factorString分解为一个因子“factor”,每个因子由该因子所对应的运算类型、所含参数、因子指数等构成,如果因子之间的分隔符为“/”,分隔符后的因子指数乘以-1。
1.2.2表达式数值计算过程
表达式计算过程如图2所示。
第一步,对item中因子列表中的各个因子factor,根据factor的类型、参数、指数等的不同情况,利用递归方法,按照各自对应的计算公式计算因子factor的数值factorValue。
第二步,将item的因子列表factorList中各因子的数值计算结果factorValue相累乘,并将结果与项系数相乘得项item的数值itemValue。
第三步,项与项之间的运算结果相加得到表达式expression的数值expressionValue。
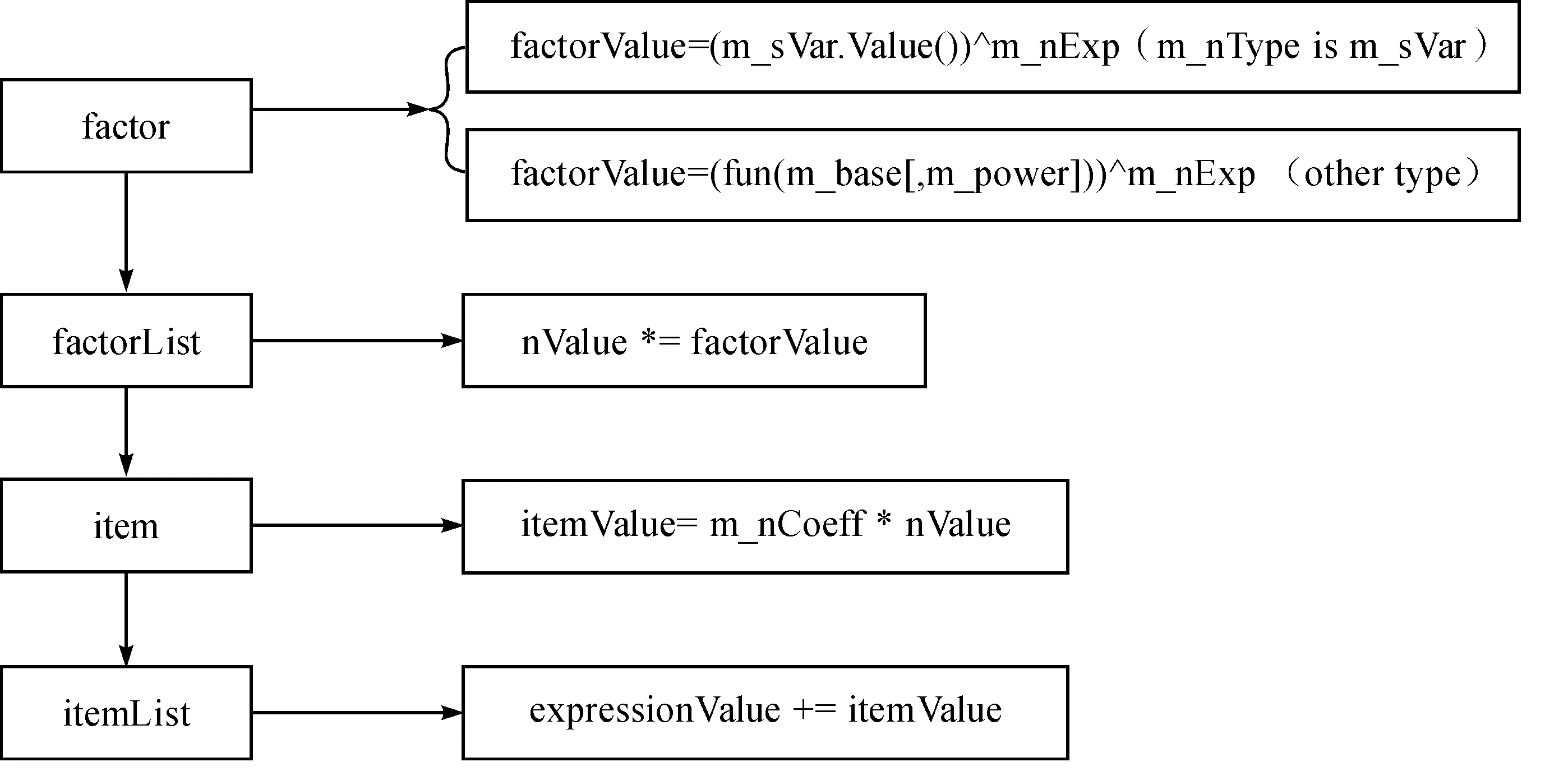
图2 表达式计算图Fig.2 Calculation of expression
图2中,factorValue的计算过程中fun是指运算函数,可由factor的类型m_nType解析而得,包括三角函数、反三角函数、对数运算等基本初等运算。变量型factor的计算过程为:系统通过搜索当前文档中所包含的变量列表查看待计算的变量是否已经存在,如果不存在,则给其赋值为随机值,并将其存入变量列表;如果已经存在,则获取其对应的数值给当前变量。
2实例
基于几何对象的代数化和含参数的代数表达式解析及计算算法可实现平面动态几何系统中,解析几何模块功能的融合,例如,如果函数的解析式是一个含参数的初等代数表达式,系统可通过计算在某区间内以一定的步长变化的自变量的值所对应的函数值,并据此在系统所给定的逻辑坐标系中利用描点法绘制函数图像;所绘制的函数图像在平面动态几何系统中是以一个几何对象的形态出现的,因此,可通过改变函数解析式中除自变量外的其他参数的值,动态观察函数图像的变化情况,便于使用者观察、学习和研究函数形态,包括函数的单调区间、函数的极值、间断点情况等。除此之外,利用几何对象的代数化和表达式计算系统可提高平面动态几何系统中几何对象的作图效率,是平面动态几何系统中构造作图方法的重要补充,例如,绘制各类型的交点可归结为求解方程组问题,再如,过直线外一点作已知直线的平行线(垂线)的方法并不适用尺规作图方法来构造平行线,而是通过解析几何中已知点的坐标及2条直线的方程之间的关系直接求得待作直线的代数属性,并根据代数属性获得该直线的方程表达式,并据此构造直线。
在融合了解析几何模块的平面动态几何系统中,可实现含参数初等运算表达式的数值计算、函数图像绘制、各类型交点坐标计算及绘制、点的轨迹绘制等功能。
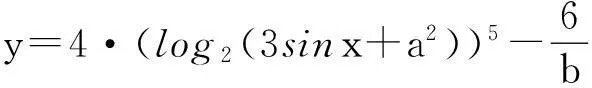
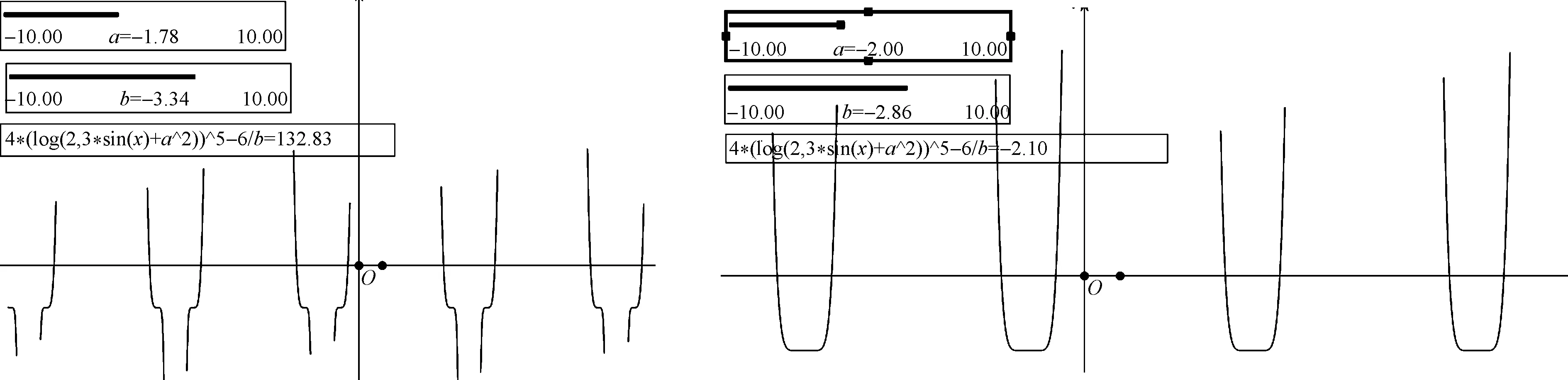
图3 表达式exp的计算结果及函数图像Fig.3 Value of expression exp and image of function y=exp
例2圆与直线的交点的构造
在平面动态几何系统中构造一条直线AB和一个圆O,选定这2个几何对象作为父对象构造交点,在具备代数表达式计算模块的平面动态几何系统中可通过如下过程实现交点的构造。
第一步,获取2个父对象的代数属性,其中直线AB的代数属性表示为a1、b1;圆O的代数属性表示为a2、b2、c2、d2、e2、f2,其中b2为0。
第三步,针对x1,x2分别计算表达式a1x1+b1和a1x2+b1的值得到y1,y2,(x1,y1)和(x2,y2)即为2个交点的代数属性。
第四步,在交点的代数属性的基础上完成点的构造。
由于父对象的代数属性会随着其位置等属性变化而变化,因此通过上述过程计算而得的交点的代数属性也随之变化,从而交点位置也随父对象的位置变化而变化,包含退化情况,如图4所示。
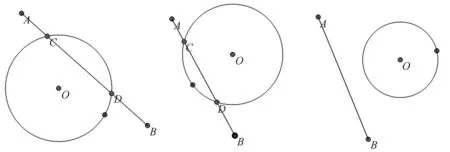
图4 直线与圆的交点变化情况Fig.4 Change of intersection points between straight line and circle
例3构造坐标点P(x,x2),观察当x在一定范围内变化时点P的运动轨迹构造方法:在系统中选择构造坐标点,在所弹出的对话框中输入x坐标为x,y坐标为y,x拖动参数为x,完成点P的构造;再选择点P,选择“跟踪”功能;拖动点P,观察发现点P的运动轨迹为抛物线,如图5所示。
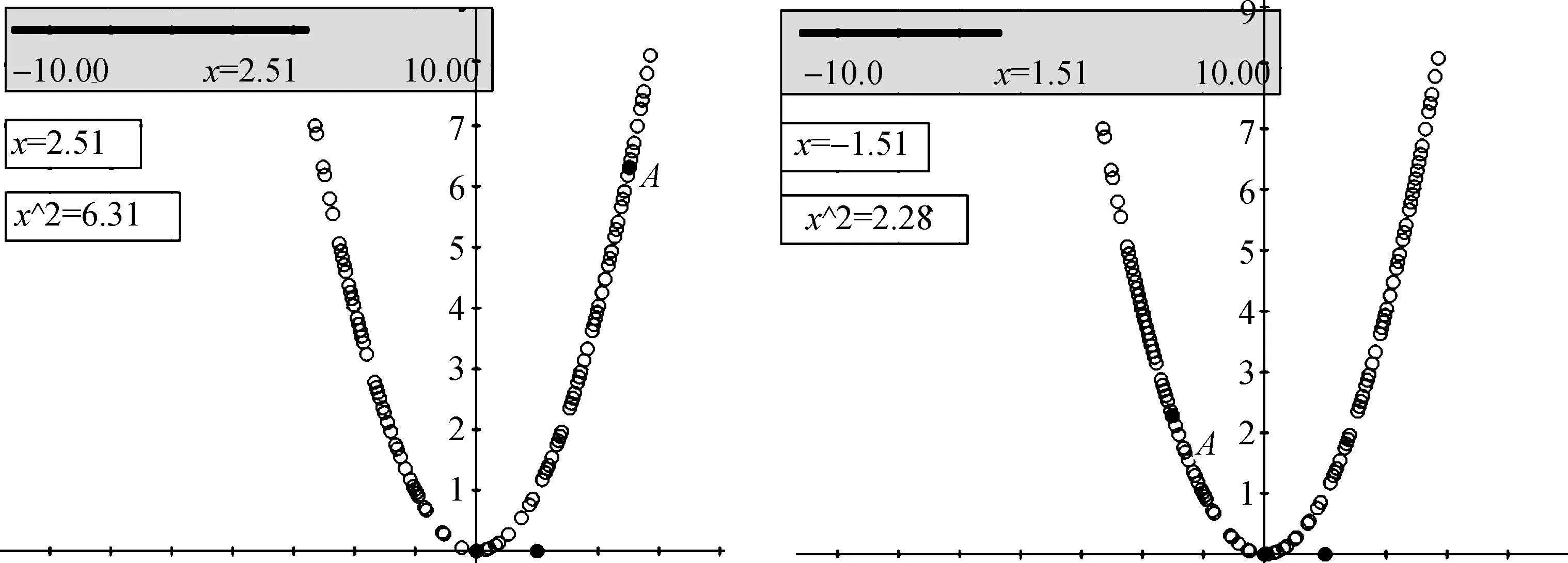
图5 坐标点P(x,x2)的坐标计算和轨迹Fig.5 Values of coordinates and locus of point P(x,x2)
3结语
将平面动态几何系统中的几何对象代数化,并设计相应的含参数代数表达式的计算算法,就可以很好地将平面解析几何模块融入平面动态几何系统中,从而提高几何图元的构造效率,提高了系统的操作便捷性和直观性,丰富了系统的功能。在此基础上,可进一步研究发展更复杂形式的表达式计算算法,以及面向三维动态几何系统解析几何模块。
参考文献:
[1]JACKIW N. The geometry’s sketchpad[CP/DK]. Berkely: Key Curriculum Press, 1991.
[2]ZHANG J Z, LI C Z. An introduction to logical animation[C]//Computer Algebra and Geometric Algebra with Applications: 6th International Workshop.Berlin Heidelberg: Springer, 2005: 418.
[3]HOHENWARTER J, HOHENWARTER M, LAVICZA Z. Introducing dynamic mathematics software to secondary school teachers: the case of geogebra[J]. Journal of Computers in Mathematics and Science Teaching,2009,28(2):135.
[4]LABORDE J, BELLEMAIR F. Gabri-Geometry II[CP/DK]. Dallas: Texas Instruments, 1993.
[6]IPEK J, ORHAN S, AKBASOGLU R, et al. Math teachers’ geometry learning and teaching with dynamic geometry programs[J]. Global Journal of Information Technology, 2014, 4(2): 44.
[8]万剑.几何画板在初中二次函数教学中的应用研究[D].南昌:南昌大学,2013.
[9]庄振林.几何画板在高中解析几何教学中的应用研究[D].呼和浩特:内蒙古师范大学,2013.
[10]张景中,彭翕成.函数作图软件的评价和选择[J].数学通报,2007,46(8):1.
[11]张景中,江春莲,彭翕成.基于《超级画板》开设《动态几何》课程的实践与思考[J].数学教育学报,2008,17(5):1.
[12]张传军,杨跃鸣,刘军明.Z+Z智能教育平台超级画板的发展之我见[J].电脑知识与技术,2014,10(15):3626.
[13]严蔚敏,吴伟民.数据结构(C语言版)[M].北京:清华大学出版社,2011:52-54.
[14]何云东,黄昶.复杂表达式解析和计算的研究实现[J].中国科技信息,2009(8):34.
[15]狄光智,杨为民,张雁.通用表达式计算中的关键问题研究[J].现代计算机,2009(4):29-31.
[16]张秀深,杨威.一种用于脚本解释器的表达式计算算法探究[J].山西师大学报(社会科学版),2012,39(增4):194.
Study of elementary algebraic expression calculation based on dynamic geometry system
CHEN Xiaoxia1,2
(1. School of Sciences, Zhejiang University of Science and Technology, Hangzhou 310023, China; 2.National Engineering Research Center for E-Learning, Central China Normal University,Wuhan 430079, China)
Abstract:Based on the algebraic characteristics of the geometry object in the plane dynamic geometry system, we use tree structure and stack method to analyze and calculate the parameters of the algebraic expression, to build a plane dynamic geometry system with the module of algebraic expression calculation with parameter. The plane dynamic geometry system can combine with the analytical geometry very well, which enriches the function and improves the operation efficiency of the plane dynamic geometry system.
Keywords:plane geometry; dynamic geometry; plane analytical geometry;algebraic expression
中图分类号:O182; TP301.6
文献标志码:A
文章编号:1671-8798(2016)01-0001-06
作者简介:陈晓霞(1978—),女,山西省潞城人,讲师,博士研究生,主要从事机器证明、几何约束求解理论等研究。
收稿日期:2015-10-19
doi:10.3969/j.issn.1671-8798.2016.01.001
浙江科技学院学报,第28卷第1期,2016年2月
Journal of Zhejiang University of Science and Technology
Vol.28 No.1, Feb. 2016

