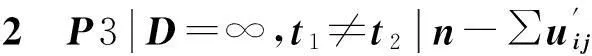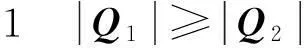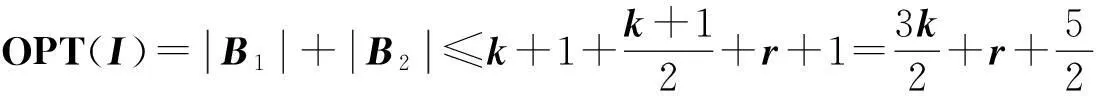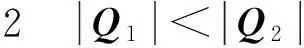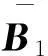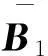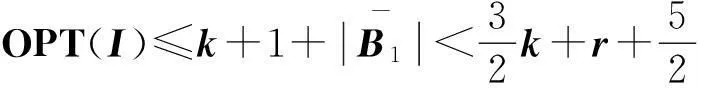机器带故障的三台机排序问题的两个近似算法
叶赛英,徐弼军
(浙江科技学院 理学院,杭州 310023)
机器带故障的三台机排序问题的两个近似算法
叶赛英,徐弼军
(浙江科技学院 理学院,杭州 310023)
摘要:机器带故障的m台机的目标函数为最小化误工工件数的排序问题,在m≥2时是NP(nondeterministic polynomial)困难的问题,对m=3,当工件转移时间t=0和t≠0两种情况,提出了和的近似算法,以及对应的渐进性能比,且证明了其界是紧的。
关键词:排序;性能比;最小化误工工件数;机器带故障中断;近似算法
在经典的平行机排序问题中,通常要求多台机器性能完全相同,给定一个任意的等待加工的工件集,在满足特定的约束条件下,求解一个排序,使给定的某个目标函数最优。单台机下的误工工件数最小化的问题是有最优算法的,按照Moore 算法可以得到问题的最优解[1-2]。如果考虑两台平行机,由于意外或不可抗力导致其中一台机器发生故障中断,那么,在该机器上加工的工件只能转移到另外一台正常工作的机器上去加工[3],在目标函数为最小化误工工件数要求下,该问题是NP(nondeterministic polynomial)困难的[4],文献[5-7]给出了不同情况下两台机带故障的近似算法。由于两台机问题是NP困难的,从而三台机问题也是NP困难的[8],本研究讨论三台机带故障中断下,目标函数为误工工件数最小化的问题。
1问题的提出
现有三台相同的机器,将三台机器上正在加工的工件集设为:
I={J11,J12,…,J1n1;J21,J22,…,J2n2;J31,J32,…,J3n3},
其中,Jij为中断前计划在机器Mi上加工的第j个工件,加工时间为pij,n1+n2+n3=n。设机器Mi在初始的0时刻发生故障中断,且中断的持续时间很长,在该机器上未完工的工件不可能等待机器恢复正常后再加工,不妨设中断时长D=∞,构造0—1变量
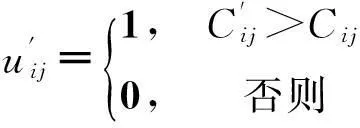
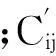
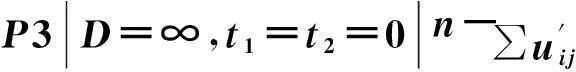
定义1设在中断发生时机器上正在加工的工件为跨越工件。
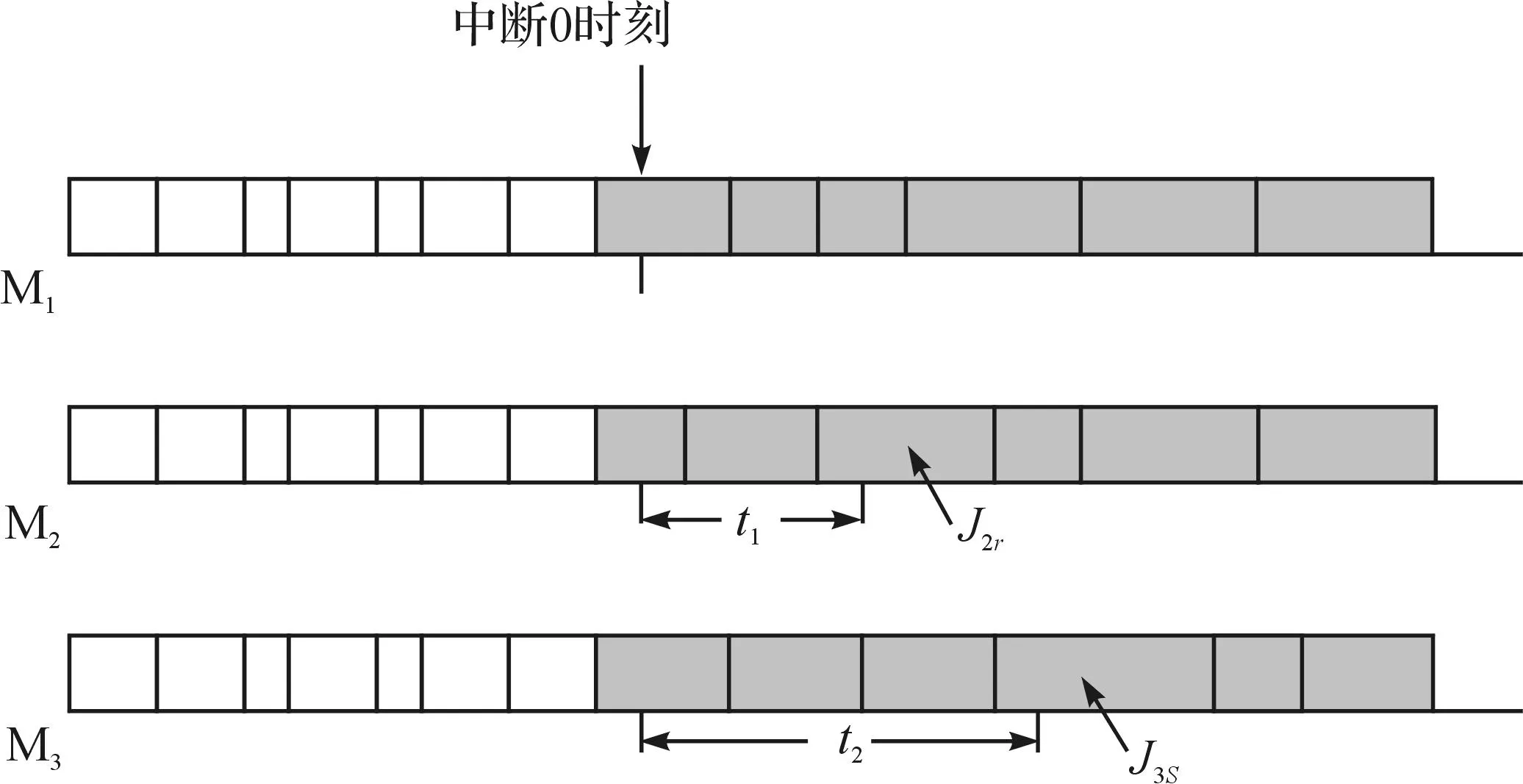
当中断发生时M1上未完成的工件集为S1,M2上的跨越工件为J2r,M2上未完成的工件集为S2,M3上的跨越工件为J3s,M3上未完成的工件集为S3。如图1所示,其中灰色为中断时三台机上未完成的工件。

图1 机器M1,M2,M3上原排序Fig.1 Original scheduling of machine M1,M2,M3
先考虑转移时间为t1=t2=0的情况。
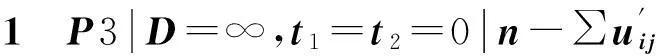
1)将工件集I1=S1∪S2∪S3按交工期限的单调非减顺序排好;将排好序的工件按Moore算法依次分配给M2加工,记在M2上按期完工工件集为P2;将I1P2中工件按Moore算法依次分配给M3加工,记M3上按期完工工件集为P3;最后将I1{P2∪P3}中的工件以任意顺序安排给M2或M3加工(M2先加工S2P2中工件,M3先加工S3P3中工件),对应序记为σ1。
2)将工件集I2=S1∪(S2{J2r})∪S3按交工期限的单调非减顺序排好;将排好序的工件按Moore算法依次分配给M2在工件J2r后加工,记M2上按期完工工件集为D2;将I2D2中工件按Moore算法依次分配给M3加工,记M3上按期完工工件集为D3。最后将I2(D2∪D3)中工件以任意顺序安排给M2或M3加工(M2先加工S2D2中工件,M3先加工S3D3中工件),对应序记为σ2。
3)将工件集I2=S1∪S2∪(S3{J2s})按交工期限的单调非减顺序排好;将排好序的工件按Moore算法依次分配给M2加工,记M2上按期完工工件集为E2;将I2E2中工件按Moore算法依次分配给M3在工件J3s后加工,记M3上按期完工工件集为E3。最后将I2(E2∪E3)中工件以任意顺序安排给M2或M3加工(M2先加工S2E2中工件,M3先加工S3E3中工件),对应序记为σ3。
4)将工件集I2=S1∪(S2{J2r})∪(S3{J3s})按交工期限的单调非减顺序排好;将排好序的工件按Moore算法依次分配给M2在工件J2r后加工,记M2上按期完工工件集为F2;将I2F2中工件按Moore算法依次分配给M3在工件J3s后加工,记M3上按期完工工件集为F3。将I2(F2∪F3)中工件以任意顺序安排给M2或M3加工(M2先加工S2F2中工件,M3先加工S3F3中工件),对应序记为σ4。
证明设在算法1中σi(1≤i≤4)下的M2上按期完工工件集为{Jp1,…,Jpk},而由算法1最终得到的M2上按期完工工件集至多为A1={Jp1,…Jpk+1},在算法1中σi(1≤i≤4)下的M3上按期完工工件集为Jq1,…,Jqr,由算法1最终得到M3上按期完工工件集至多为A2={Jq1,…Jqr+1}。

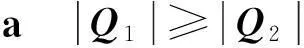
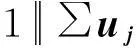
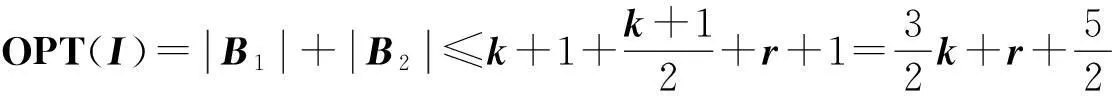
(1)
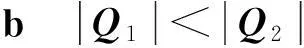
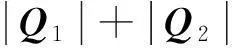
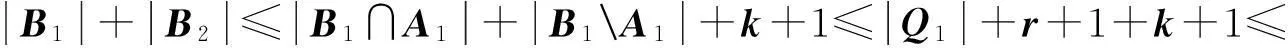
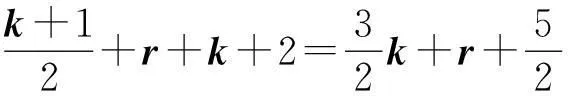
(2)
综上所述,总有
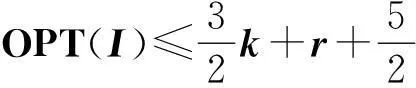
(3)
又由

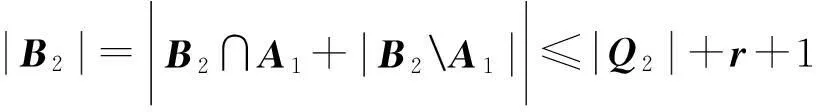
则
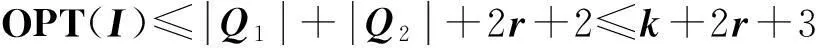
(4)
综合式(3)、(4)得
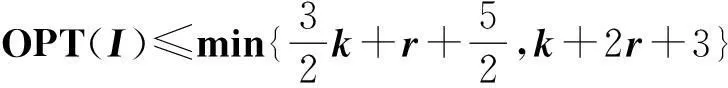
(5)
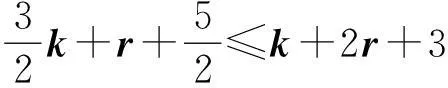
此时,
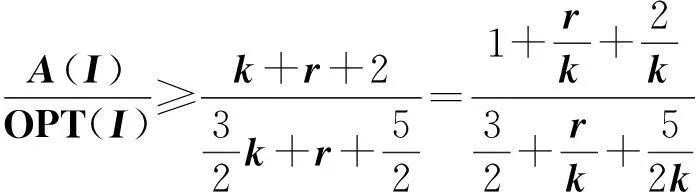
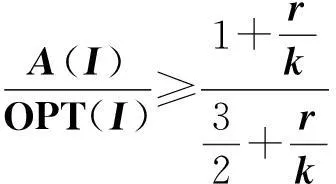
(6)
式(6)成立。

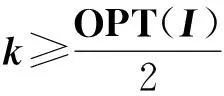
故当OPT(I)→+∞时,必有k→+∞,∀ε>0,∃正整数N;当OPT(I)≥N时,必有

(7)
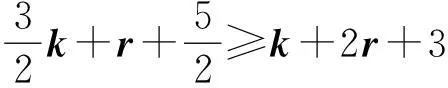
此时,
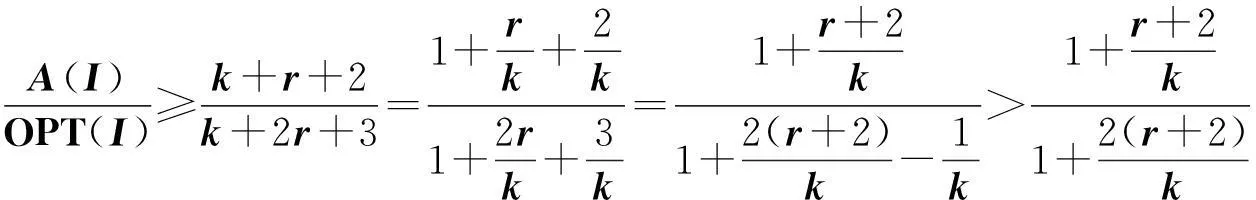
(8)
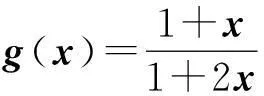
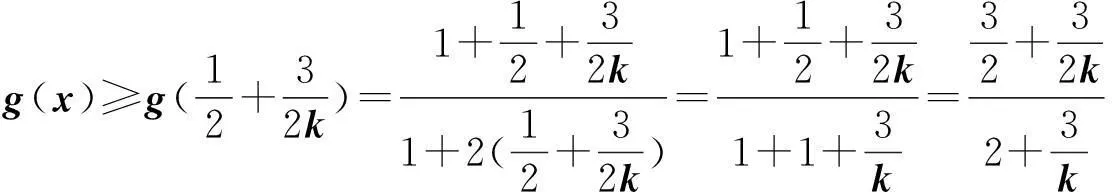

上述证明说明,不论何种情况发生,总有

(9)

证明设M2,M3上无跨越工件,设中断发生时三台机未完成工件依原最优序排列为,S1={J11},S2={J21,J22},S3={J31,J32},p31=1,p11=p21=p22=2,p32=4,由此可知,C11=C21=2,C22=4,C31=1,C32=5。
按算法1,将J31,J22安排在M2上加工,J11安排在M3上加工,J21,J32为误工工件,以任意序最后安排在M2或M3上加工。
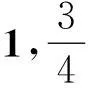
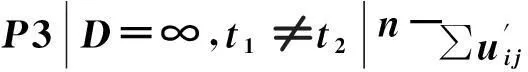
考虑t1≠t2的情况,为不失一般性,不妨设t1 设机器M1在0时刻发生中断,中断发生后,一方面,由于M1上未完成的工件转移到当中其他一台机器,最快也要t1时刻,从而机器M1上按原序所安排的t1时刻之前开工的工件没来得及转移就已经误工了,由此只需要考虑M1上按原序所安排的t1时刻之后加工的工件。另一方面,由于t2>t1,机器M1上原序所安排的t1时刻之后且t2时刻之前开工的工件来不及转移就已经误工了,把这些来不及开工的工件记为哑工件,并记这些工件组成的集合为R。 记M1上t1时刻未完成的工件组成工件集为S1,在t1时刻机器M2上未完成的工件集为S2,此时设M2上的跨越工件为J2r,在t2时刻机器M3上未完成的工件集为S3,此时设M3上的跨越工件为J3s。如图2所示,其中灰色为中断时三台机上未完成的工件。 图2 机器M1,M2,M3上原排序Fig.2 Original scheduling of machine M1,M2,M3 1)将工件集I1=S1∪S2∪S3按交工期限的单调非减顺序排好;在t1时刻将排好序的工件按Moore算法依次分配给M2加工(若首个工件为J2r,则继续,不中断之),记在M2上按期完工工件集为P2;将I1(P2∪R)中工件在t2时刻按Moore算法依次分配给M3加工(若首个工件为J3s,则继续,不中断之),记在M3上按期完工工件集为P3;最后以任意顺序安排给M2或M3加工I1{P2∪P3}及所有哑工件,对应序记为σ1。 2)将工件集I1=S1∪(S2{J2r})∪S3按交工期限的单调非减顺序排好;在C2r时刻将排好序的工件按Moore算法依次分配给M2加工,记在M2上按期完工工件集为D2;将I1(D2∪R)中工件在t2时刻按Moore算法依次分配给M3加工(若首个工件为J3s,则继续,不中断之),记在M3上按期完工工件集为D3;最后以任意顺序安排给M2或M3加工I1{D2∪D3}及所有哑工件,对应序记为σ2。 3)将工件集I1=S1∪S2∪(S3{J3s})按交工期限的单调非减顺序排好;在t1时刻将排好序的工件按Moore算法依次分配给M2加工(若首个工件为J2r,则继续,不中断之),记在M2上按期完工工件集为E2;将I1(E2∪R)中工件在C3s时刻按Moore算法依次分配给M3加工(若首个工件为J3s,则继续,不中断之),记在M3上按期完工工件集为E3;最后以任意顺序安排给M2或M3加工I1{E2∪E3}及所有哑工件,对应序记为σ3。 4)将工件集I1=S1∪(S2{J2r})∪(S3{J3s})按交工期限的单调非减顺序排好;在C2r时刻将排好序的工件按Moore算法依次分配给M2加工,记在M2上按期完工工件集为F2;将I1(F2∪R)中工件在C3s时刻按Moore算法依次分配给M3加工,记在M3上按期完工工件集为F3;最后以任意顺序安排给M2或M3加工I1{F2∪F3}及所有哑工件,对应序记为σ4。 证明分两种情况讨论。 故 (10) (11) 综上所述,不管发生何种情况,不等式 (12) 总成立,而A(I)=(k+1)+(r+1),故此时必有 定理证毕。 4算法的计算复杂性 Moore算法复杂性为O(nlogn),由于算法1中4次利用Moore算法,从而算法1的时间复杂性为O(nlogn)。算法2也是4次利用Moore算法,从而算法2的时间复杂性仍为O(nlogn)。 5结语 目前在机器故障中断的问题上,国内外相关研究成果并不太多,而该问题具有广泛的现实意义,且待研究的问题还有很多。笔者认为,可以结合机器有不同就绪时间的问题和工件有就绪时间的问题,在P(polynomial)问题上寻求新的最优算法及对NP困难问题寻求更好的近似算法。 参考文献: [1]MOOREJM.Annjob,onemachinesequencingalgorithmforminimizingthenumberoflatejobs[J].ManagementScience,1968,15(3):102. [2]王方,赵传立.具有学习效应的且加工时间可控的单机排序问题[J].沈阳师范大学学报(自然科学版),2013(4):471. [3]唐国春,张峰,罗守成,等.现代排序论[M].上海:上海科学普及出版社,2003. [4]LEECY,YUG.Singlemachineschedulingunderpotentialdisruption[J].OperationsResearchLetters,2007(35):1. [5]沈灏,杨启帆.两台机器及时完工工件数最大化问题的近似算法[J].高校应用数学学报:A辑,2003,18(2):207. [6]叶赛英,沈灏,魏小兰.机器带故障的两台机排序问题的一个近似算法[J].杭州电子科技大学学报,2008,28(2):90. [7]叶春花,沈灏.机器带中断的误工问题的近似排序算法[J].杭州电子科技大学学报,2010,30(1):96. [8]魏飞,刘守鹏.工件带拒绝费用的三台单机排序问题研究[J].山东科学,2013(6):9. [9]卢开澄.算法与复杂性[M].北京:高等教育出版社,1995. Two approximation algorithms for three parallel machines scheduling with machine disruptions YE Saiying, XU Bijun (School of Sciences, Zhejiang University of Science and Technology, Hangzhou 310023, China) Abstract:We discuss the problem of m parallel machines scheduling with disruptions with the objective of minimizing the sum of unit penalties. If m≥2, the problem is NP-hard. When m=3 and transfer time is t=0 and t≠0, two approximation algorithms are proposed for the problems of and respectively. And the paper proves that the upper bound is tight respectively. Keywords:scheduling; worst-case ratio; minimizing the sum of unit penalties; machine disruptions; approximation algorithm 中图分类号:O223 文献标志码:A 文章编号:1671-8798(2016)01-0012-07 作者简介:叶赛英(1980—), 女, 浙江省松阳人, 讲师, 硕士, 主要从事排序问题研究。 基金项目:浙江省《基础数学》重点学科建设学术研究子项目(20131029) 收稿日期:2015-11-01 doi:10.3969/j.issn.1671-8798.2016.01.003 浙江科技学院学报,第28卷第1期,2016年2月 Journal of Zhejiang University of Science and Technology Vol.28 No.1, Feb. 2016