材料力学梁弯曲理论在结构概念设计中的应用

文献民，姜鲁珍

(浙江科技学院 a.中德工程师学院；b.经济与管理学院，杭州 310023)



材料力学梁弯曲理论在结构概念设计中的应用

文献民a，姜鲁珍b

(浙江科技学院 a.中德工程师学院；b.经济与管理学院，杭州 310023)

摘要:基于梁的弯曲理论与结构概念设计的关系，采用静力等效的方法分析了弯矩和剪力的作用效应；同时，结合梁、平面桁架和网架等典型的工程结构，阐述了概念设计的过程和能够解决的问题。实践表明，该方法可以根据构件的弯矩图和剪力图提出其正确的概念设计方案，能够提高学生运用梁的弯曲理论对构件或结构进行概念设计的能力，能够促进对钢筋混凝土设计原理和钢结构设计原理的学习；是对材料力学传统教学方法的改革和补充。

关键词:概念设计；材料力学；弯曲理论；剪切理论

在土木工程中，结构及结构构件的概念设计是指根据设计对象的内力情况，运用力学原理和理论提出的关于材料、截面选型、工程造价、环境保护等问题的解决方案。好的概念设计是指在符合力学原理的基础上，使设计对象造价最小、结构自重最小、环境代价最小。概念设计是整个设计环节中的最重要的第一步，在土木工程领域流传的一句经典名言是“想清楚比算得准确更重要”，说的就是概念设计在设计过程中的重要地位。

在与德国应用科学大学土木工程专业联合培养本科生项目的合作过程中，深刻地感受到中、德高校在应用型人才培养方面的差距和不同，仅仅从土木工程专业的力学课程的教学内容、手段和方法等方面进行比较，中方教师比较重视力学理论知识的传授，往往不太重视力学理论在土木工程实际中的应用[1-3]，特别是没有注意到如何运用所学理论对结构或者构件进行概念设计。其结果是：与土木工程实际问题相关的内容不多，学生对力学课程的学习兴趣不高；在钢筋混凝土设计原理及钢结构设计原理等后续课程的学习中[4-5]，学生不会利用学习过的理论知识去理解各种规范和构造要求；学生不能够运用力学理论对桁架、网架及高层建筑等结构进行概念设计。

在借鉴德国高校应用型人才培养经验的基础上，笔者对浙江科技学院与德国吕贝克应用科学大学联合培养土木工程专业本科生项目的力学课程的教学模式和方法进行了一些改革和创新，其重点在于借助构件及结构的概念设计，引导学生从一个新的视角正确认识和理解受弯构件的基本力学理论，进而提高学生发现问题、分析和解决实际问题的能力，同时促进后续钢筋混凝土设计原理及钢结构设计原理等重点专业课程的学习。

1梁弯曲理论与构件的概念设计

在材料力学的教学中，主要是围绕轴心受拉(压)构件、受扭构件和受弯构件开展教学活动，学习的内容是构件的强度、刚度等问题的基本理论及相应公式。作为结构中最常见的设计对象，受弯构件的力学理论不仅在解决构件强度和刚度问题中发挥了作用，更重要的是在构件及结构的概念设计中起到了决定性的作用。因此，学习如何运用梁的弯曲理论和剪切理论对构件及结构进行概念设计是非常重要的。受弯构件的基本理论与构件及结构概念设计之间的关系如图1所示。

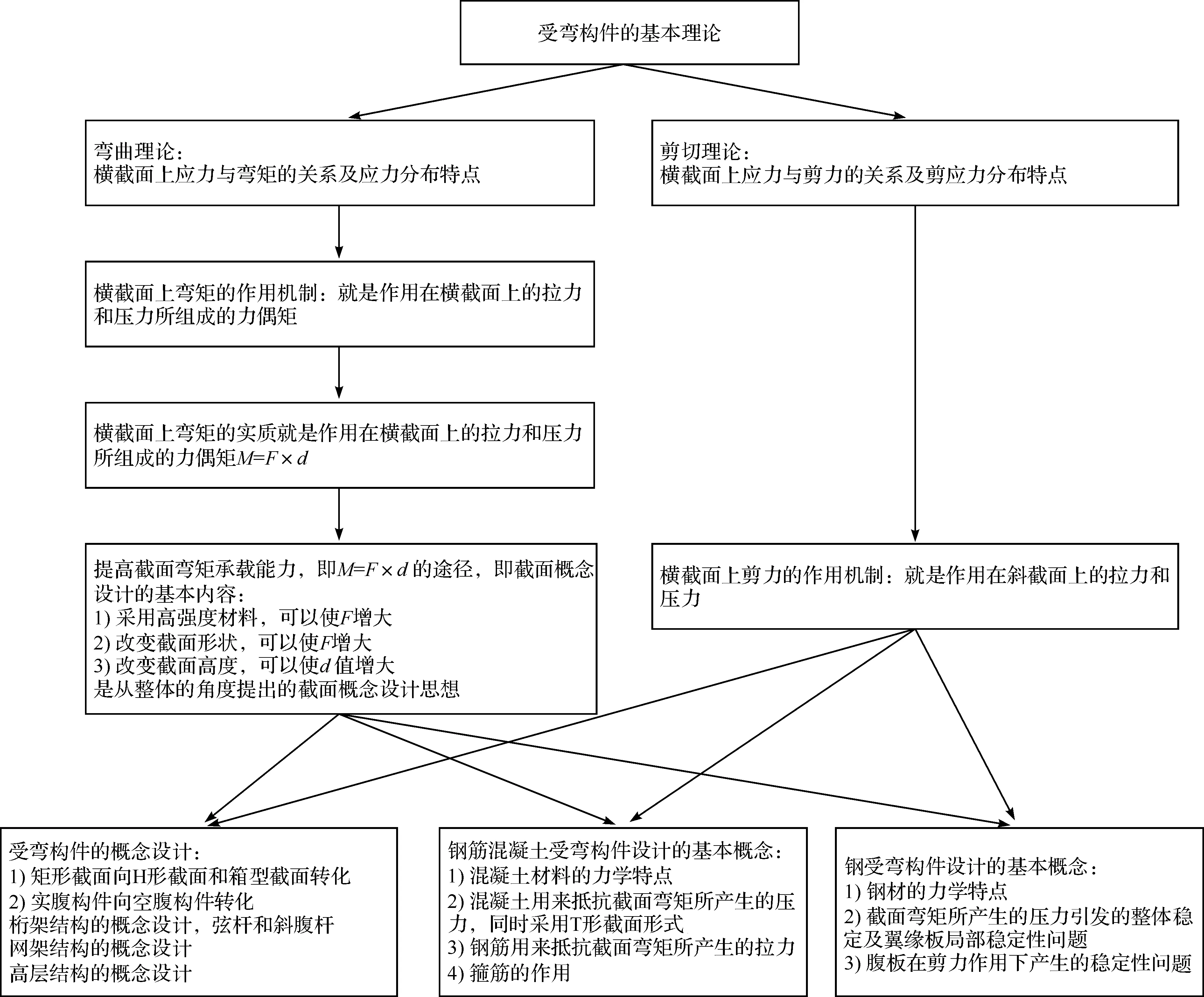
图1　弯曲理论与结构的概念设计Fig.1　Bending theory and concept design of structure

1.1弯矩作用的效应及静力等效

在弯矩作用下，构件横截面将产生弯曲正应力，其计算公式为

(1)

正应力沿截面高度线性变化。以矩形双轴对称截面为例，其分布特点如图2(a)所示，正应力的作用方向与横截面垂直，一部分使横截面受压，另一部分使横截面受拉。按照静力学等效方法，可以求出这些拉、压应力的合力F的大小及其作用点位置，其作用点位于左、右对称轴y上，并且距离顶部和底部均为1/6截面高度，假设两个作用点之间的距离为d，那么作用于横截面上的力矩M与偶矩F×d等效，如图2(b)所示。

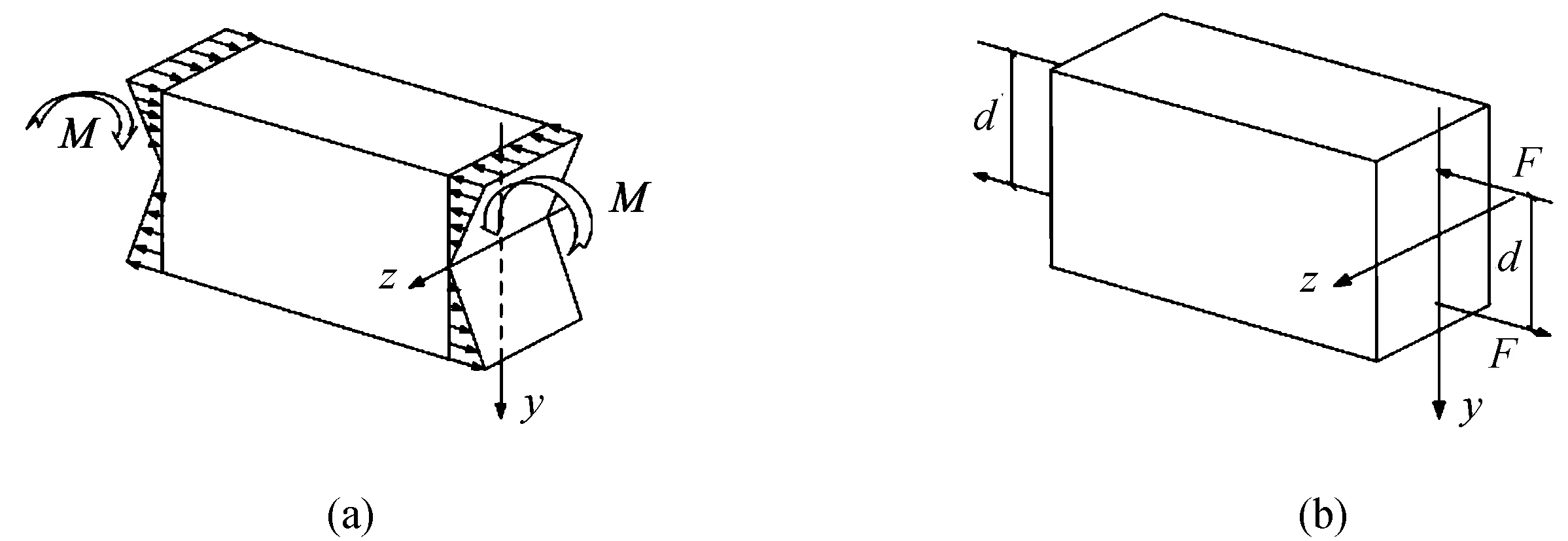
图2　弯矩作用下横截面正应力分布及等效力偶Fig.2　Transverse normal stress distribution under action of bending moment and equivalent couple

1.2剪力作用的效应及静力等效

在剪力作用下，构件横截面将产生剪应力，其计算公式为

(2)

剪应力作用于横截面内，沿截面高度分布规律为二次曲线，如图3(a)所示，根据静力学平衡条件，可以求出原始单元体所对应的主单元体上的主应力如图3(b)所示。可以看出，受剪应力作用的原始单元体可以等效成为在一对拉应力和一对压应力共同作用下的单元体，单元体呈现出拉、压共同作用的变形特征。

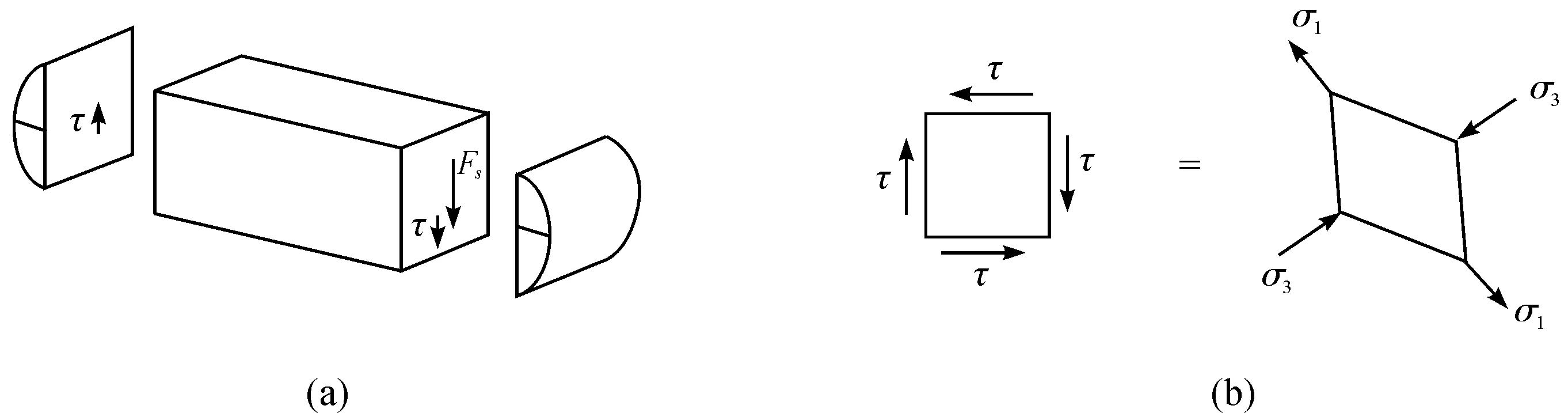
图3　作用于横截面上的剪应力及其作用结果Fig.3　Results of shear stress acting on cross section and its effects

综上所述可以得到以下结论：在横向荷载作用下的受弯构件，其横截面上产生的弯矩和剪力最终都可以等效为拉力和压力，并且这些拉力和压力与梁的弯矩和剪力的大小成正相关性，它们是受弯构件概念设计的基本依据和参考要素。

2受弯结构的概念设计讨论

根据以上的分析和总结，本文列出了利用梁的弯曲理论和剪切理论对构件及结构进行概念设计的基本思路，如图1所示，并应用于中德工程师学院土木工程专业的教学中，取得了一些经验。为了便于说明，下面的讨论均以简支梁在均布荷载作用下的内力图为背景，简支梁在均布荷载作用下的弯矩和剪力如图4所示。

2.1H形和工字形截面构件的翼缘板和腹板的作用分析及概念设计

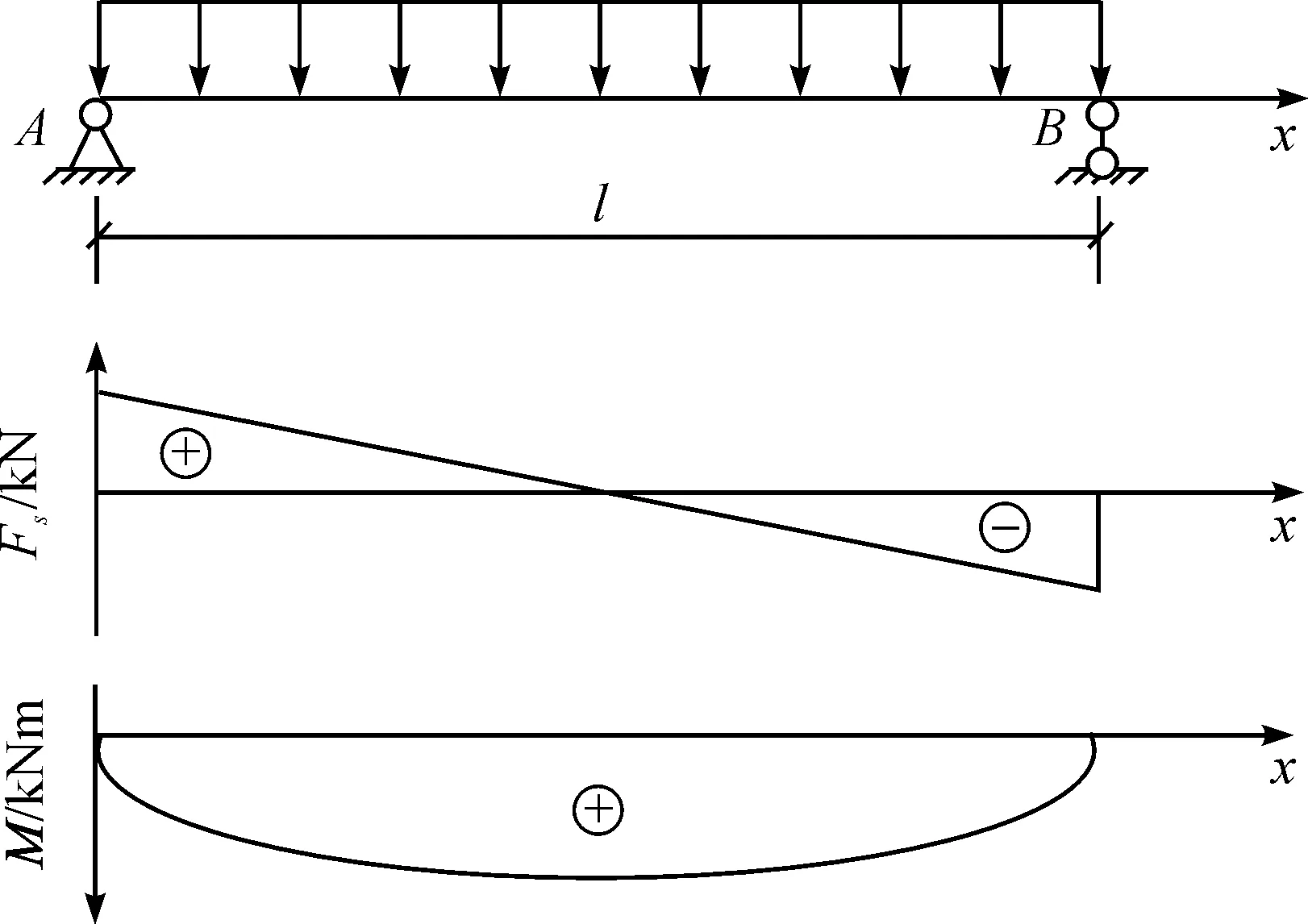
图4　简支梁在均布荷载作用下的弯矩和剪力Fig.4　Bending moment diagram and shear force diagram of simply supported beam under uniformly distributed loading

H形截面或者工字形截面构件在弯矩和剪力作用下产生的正应力和剪应力的分布规律如图5(a)和图5(b)所示，按照上述分析方法对应力进行积分可以发现：横截面上的弯矩主要由上、下翼缘板承担，弯矩的正负决定了上、下翼缘板承受拉力还是压力，本例中，在正弯矩作用下，梁的上翼缘板受压，下翼缘板受拉，并且越靠近跨中，翼缘板承受的拉力和压力越大；而横截面上的剪力则主要由腹板承担，根据图2(b)可以发现，在剪力作用下，腹板两个正交的方向受压和受拉，受压和受拉的方向与剪力的正负有关，本例中，以跨中为界，左半部分的腹板在正的剪力作用下沿-45°方向受拉，沿45°方向受压，而右半部分的腹板则正好相反，并且越靠近支座，腹板承受的拉力和压力越大。

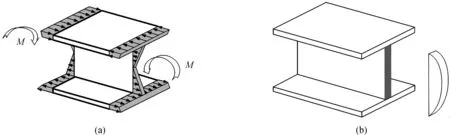
图5　H形截面受弯构件的正应力和剪应力分布Fig.5　Distribution of normal stress and shear stress of H section bending component

设计者可以根据构件的弯矩图改变受弯构件的截面高度，在保持上、下翼缘板所受压力和拉力不变的情况下，增大截面的高度可以提高受弯构件的抗弯承载力，即提高受弯构件横截面所能够承受的弯矩值。由于构件的上半部分承受压力，设计者还需要采取合理的构造措施来保证受压部分的整体稳定和翼缘板板件的局部稳定。如增加受压翼缘的的侧向支撑及减小翼缘板的自由外伸宽厚比等。

腹板在剪力的作用下所处的状态是沿-45°方向或者沿45°方向受压，因此,设计者还需要注意腹板的稳定性等问题，并采取相应的构造措施保证腹板的稳定性，如设置腹板加劲肋或者减小腹板的高厚比等。H形截面受弯构件的设计实例如图6所示。

图6　H形截面的简支梁设计实例Fig.6　Design example of simply supported beam with H section

对比图4所示简支梁内力图可以发现：在吊车梁弯矩比较大的区域，如跨中区域，吊车梁的高度较大，而在弯矩比较小的区域，如支座附近，梁的高度较小；在剪力比较大的区域，如支座附近，腹板加劲肋之间的间距比较小，在剪力比较小的区域，如跨中，腹板加劲肋的间距就比较大。

2.2桁架的弦杆及腹杆的作用分析及概念设计

当受弯构件的截面高度随所承受的弯矩的增加而达到一定时，会造成腹板面积增加，从而使构件的自重增大，造成材料的浪费。在这种情况下可以采用两种方案予以解决，第一种方案是将腹板开设孔洞，减小自重，这种方案适合于截面高度不大的受弯构件，设计实例如图7所示；第二种方案是用斜腹杆来代替腹板抵抗剪力，如果将上、下翼缘板和腹板用角钢或者钢管代替，则是一种新型的结构形式——平面桁架，设计实例如图8所示。

图7　空腹梁Fig.7　Beam with holes on web plate

图8　平面桁架Fig.8　Plane truss

根据简支梁的弯矩图可以判断上、下弦杆所承受的拉力和压力变化情况，与支座附近的弦杆相比，跨中附近的弦杆承受较大内力。对于承受压力的弦杆，需要采取构造措施保证其稳定性；同样，根据简支梁的剪力图,不仅可以判断斜腹杆的内力大小的变化情况，而且还可以判断斜腹杆是拉杆还是压杆，进一步地可以采用钢索代替受拉斜腹杆，对于受压的斜腹杆要注意其稳定性。

为了保证桁架受压上弦杆的稳定性，下面的设计实例中明显地降低了受压上弦杆的几何长度，也可以采用增加受压弦杆平面外支撑的方式保证桁架的稳定性，如图9和图10所示。

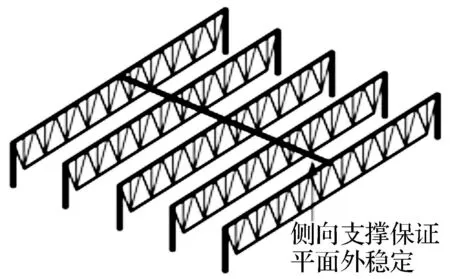
图9　平面桁架与侧向支撑Fig.9　Plane trusses and lateral support

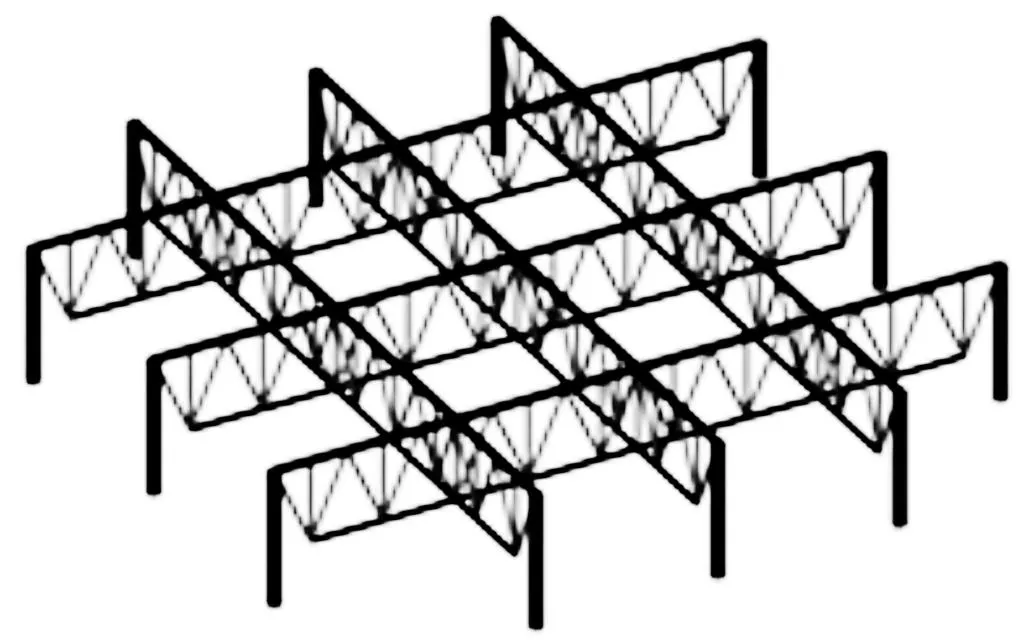
图10　正交正放桁架Fig.10　Orthogonal trusses

或者将图11(a)所示的平面桁架的受压上弦杆展开，增加上弦杆平面外的回转半径来保证桁架的稳定性，如图11(b)所示。

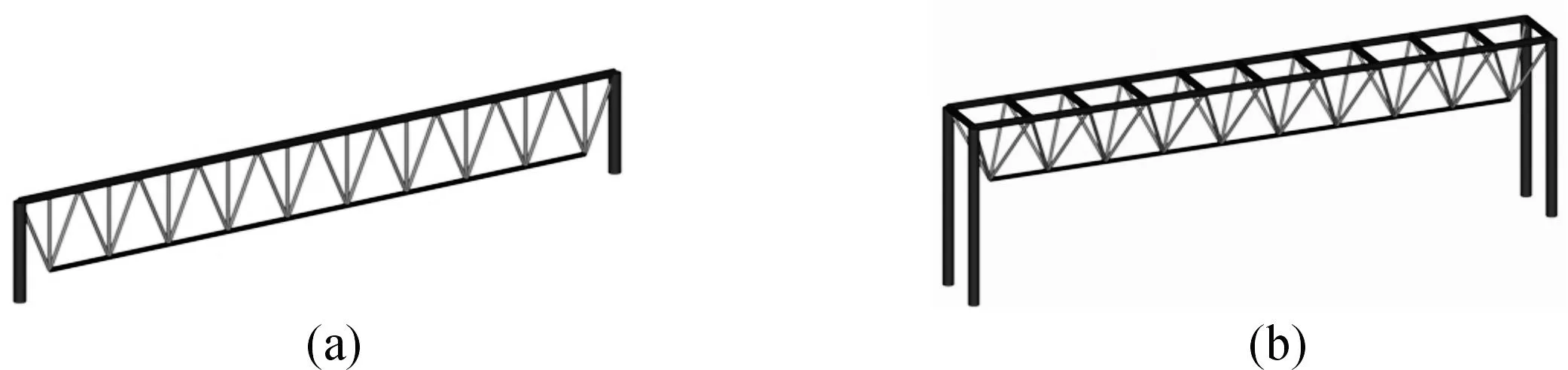
图11　平面桁架与空间桁架的对比Fig.11　Plane truss and spatial truss contrast

2.3网架的概念设计

如果建筑物要求大跨度空间，那么受弯构件的跨度就会非常大，此时弯矩也会急剧增大。为了能够保证桁架的稳定性，可以将图11(b)所示的桁架进行交叉摆放，如图12(a)所示，最终形成带有巨大空间的网架结构，如图12(b)所示。其上、下弦杆和斜腹杆的内力变化情况的判断和概念设计方法和思路同上。

图12　网架的组成Fig.12　Composition of spatial truss

3结语

通过静力等效的方法可以有助于学生充分认识和理解弯矩及剪力作用的本质，有助于学生根据受弯构件的弯矩图和剪力图以新的视角和高度来对受弯构件和结构进行概念设计。这些概念设计的内容具体包括学会如何正确地对平面桁架进行杆件布置，如何改变受弯构件截面高度，如何对各种设计方案进行分析和比较等。同时，也为后面的钢筋混凝土设计原理和钢结构设计原理等课程的学习奠定非常好的基础。

在浙江科技学院中德工程师学院土木工程专业本科生的暑期工程实践活动中，学生能够运用所学的力学知识发现和解决一些实际工程问题，取得了良好的实习效果。

在土木工程专业应用型人才培养的教学和实践过程中，力学原理在结构和构件概念设计方面起到了非常重要的作用，因此，在注重理论教学的同时，需要更加注重力学原理在结构概念设计方面的应用。

参考文献:

[1]张旭光,王秀振,李莉,等.独立学院土木专业材料力学课程实验教学研究与探讨[J].高等建筑教育，2013，22(5)：125.

[2]倪振强.普通本科院校土木工程专业材料力学课程教学探索[J].高等建筑教育，2015，24(1)：51.

[3]白志玲.对《材料力学》课程教学改革的思考[J].山东化工，2015，44(6)：123.

[4]卢会方,贺东青.土木工程专业材料力学教学与后续课程街接的探讨[J].课程教育研究，2013(19)：234.

[5]颜庆智.钢结构基本原理教学中的力学过渡[J].中国冶金教育，2012，1(l)：24.

Application of beam bending theory of material mechanics in structure concept design

WEN Xianmina, JIANG Luzhenb

(a.Chinese-German Institute of Engineering; b. School of Economics and Management,Zhejiang University of Science and Technology, Hangzhou 310023, China)

Abstract:Based on the theory of mechanics of material, the method about using the mechanical theory in the concept design of elements or structure was introduced. Firstly, the role of the nature of moment and shear force was analyzed, secondly the concept design process and attention to the problem through the typical engineering beams, truss and other structural grid were systematically exposed. Concept design is the important part of improving the ability of solving practical problems with theoretical knowledge, which can promote the learning of reinforced concrete design principles and steel structure design principles, and is the reformation and supplement for the traditional teaching method of material mechanics.

Keywords:concept design; mechanics of material; bending theory; shearing theory

中图分类号:G642.3;TU311

文献标志码:A

文章编号:1671-8798(2016)01-0072-06

作者简介:文献民(1962—)男，河南省偃师人，教授，博士，主要从事结构工程研究。

收稿日期:2015-07-01

doi:10.3969/j.issn.1671-8798.2016.01.013

浙江科技学院学报,第28卷第1期,2016年2月

Journal of Zhejiang University of Science and Technology

Vol.28 No.1, Feb. 2016