杨氏双缝干涉图样的理论模拟
杨氏双缝干涉图样的理论模拟
摘 要:本文在未经任何理论近似的情况下,模拟了杨氏双缝干涉实验中观察屏上的干涉图样,模拟结果不但有利于学生全面掌握干涉条纹的分布规律,而且有助于学生体会实验条件的重要性.
关键词:双缝干涉光程差模拟
1801年,杨氏双缝干涉实验证实了光的波动性,并首次成功测量了光的波长,为光的波动学说发展奠定了坚实的基础,因此,该实验在物理学史上具有重要的地位和作用.杨氏双缝干涉实验中,双缝到观察屏上任意点的距离差,即两光束的光程差至关重要,因为它直接决定了观察屏上干涉条纹的分布情况.
现有大学物理教材在给出观察屏上条纹分布时,大都先经过理论近似给出近似的光程差表达式[1~4],然后,将光程差表达式和光的干涉加强和减弱的条件联立,得出屏幕上干涉条纹是明、暗相间的等间隔的直条纹的结论.在近似表达式基础上得到的结论毕竟不能真实反映条纹分布,所以采用近似方法处理光程差不利于学生全面了解条纹的真实分布.观察屏上实际的条纹分布应是怎样的呢?少数教材[5]虽提到观察屏上以强度相等为特征的点的轨迹应是一组双曲线,但并未有详细说明.
本文在未经任何近似的情况下,理论模拟了观察屏上干涉明纹分布,并对条纹分布特点进行了总结.
1明暗干涉条纹所满足的方程
图1为杨氏双缝干涉实验光路示意图.
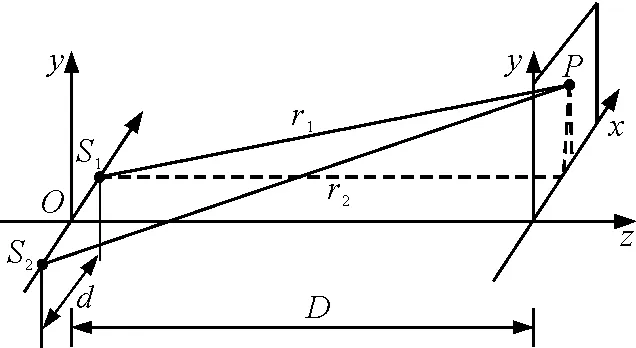
图1 杨氏双缝干涉实验光路示意图
设双缝S1,S2的间距为d,O为双缝S1,S2的中点,双缝所在平面与光屏平行.双缝与屏之间的垂直距离为D,在屏上取任意一点P,设定点P与双缝S1,S2的距离分别为r1和r2,Δr为光程差,结合图1中虚线易得
所以,双缝S1,S2发出的光到达屏上P点的光程差
Δr=r2-r1=
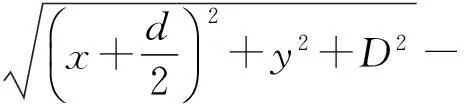
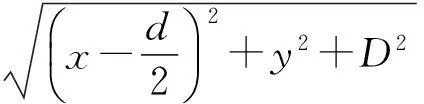
(1)
根据光的干涉的相关理论,当两光束光程差满足公式
Δr(x,y,D)=kλ,
k=0,±1,±2,…,±n
(2)
时,观察屏上满足公式(2)的点为亮点,同一k值所对应的亮点连起来构成第k级明纹.当光程差满足公式
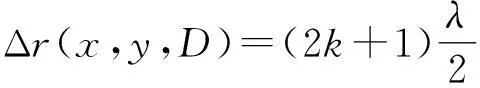
k=0,±1,±2,…,±n
(3)
时,观察屏上满足公式(3)的点为暗点,同一k值所对应的暗点连起来构成第k级暗纹.
2理论模拟结果
根据公式(1)~(3),通过改变d,D或入射波长λ值,即可获得不同条件下观察屏上的干涉条纹分布.因明、暗条纹分布情况类似,我们仅给出明纹模拟结果.在模拟过程中,入射单色光波长设为500 nm,图2~图5中的x轴和y轴分别对应图1观察屏上的x和y轴.
2.1D取不同值在较大范围内观察的情况
当d=0.1 mm,D取不同值时,在较大观察范围内,屏幕上干涉明纹的分布情况.
图2(a)~图2(d)给出了d=0.1 mm,D分别为0.5 m,1 m,1.5 m和2 m时,屏幕上较大观察范围(相对于杨氏双缝实验中通常的观察线度)内中央明纹及左右±50级明条纹的分布情况.图2中x和y轴坐标均在[-0.7 m,0.7 m]之间.
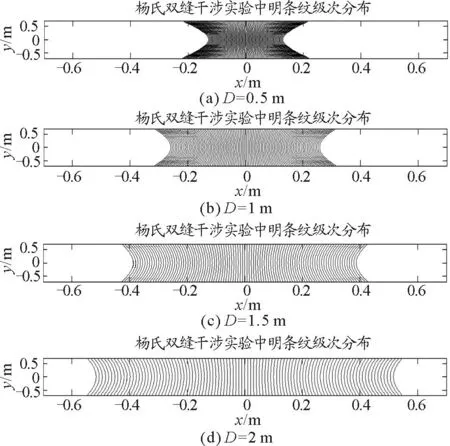
图2 d=0.1 mm,D取不同值时,屏幕上较大观察范围内明纹分布
由图2可知,观察屏上较大范围内,当D分别为0.5 m,1 m,1.5 m和2 m时,观察屏上明条纹(除中央明纹外)确实呈典型双曲线形状且对称分布在中央明纹两侧,而不是等间距的直条纹分布,但随着D的增加,双曲线的弯曲程度明显减小.另外,随着D增加,条纹间间距加大,明纹在x轴分布范围逐渐加宽.当D为0.5 m时,-50级至+50级明纹基本上分布在x轴上 [-0.2 m,0.2 m]之间,当D为1 m,1.5 m,分别分布在[-0.3 m,0.3 m]和[-0.4 m,0.4 m]之间,至D=2 m时,分布已扩展到[-0.55 m,0.55 m]之间.
2.2D取不同值在较小范围内观察的情况
当d=0.1 mm,D取不同值时,在较小观察范围内,屏幕上干涉条纹的分布情况.
图3(a)~3(d)给出了d=0.1 mm,D分别为0.5 m,1 m,1.5 m和2 m时,在较小观察范围内,观察屏上明纹分布图.图3中x轴和y轴坐标均在[-0.06 m,0.06 m]之间[图3(a)~3(d)实质分别对应图2(a)~2(d)的一小部分].
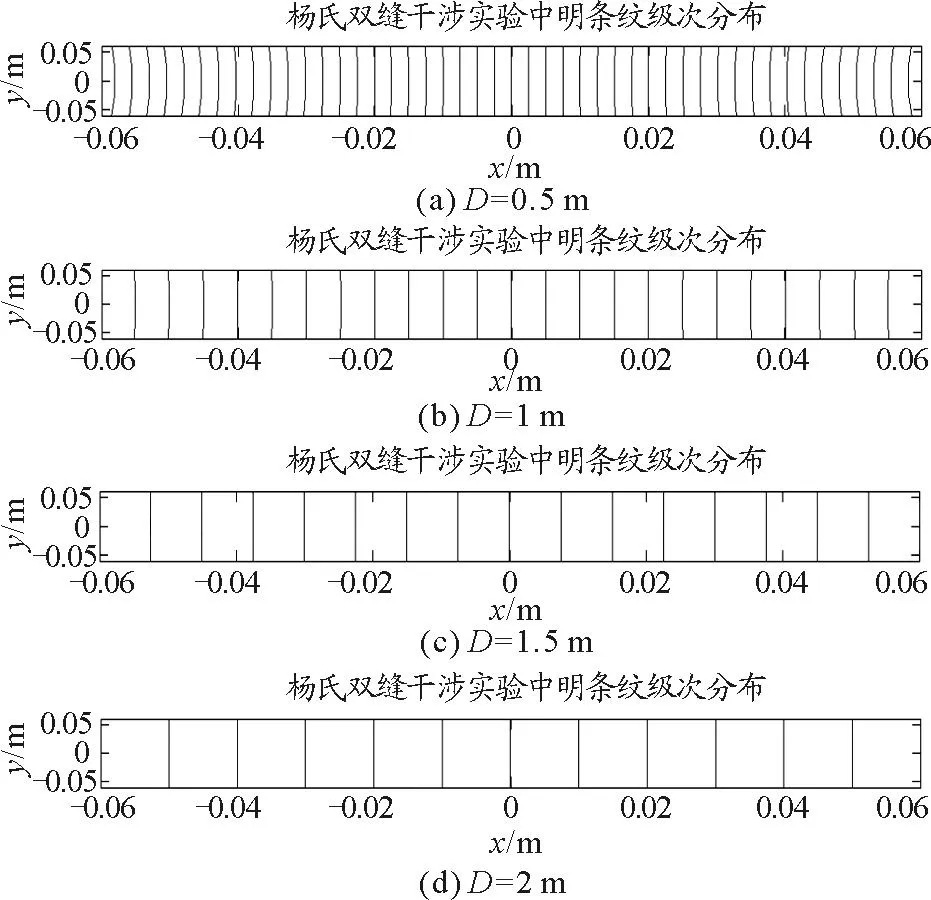
图3 d=0.1 mm,D取不同值时,屏幕上较小观察范围内明纹分布
由图3(a)~3(d)可知,在较小观察范围内,当D为0.5 m时,较高级次明纹仍呈现双曲线形,但中央明纹附近级次已非常接近直线分布.随着D增加,当D为1 m,1.5 m和2 m时,目测各级明纹均已呈平行等距直线分布.另外,随着D增加,条纹分布由密集变稀疏,条纹间距增大,观察屏上干涉明纹数量减小.当D=0.5 m时,条纹比较密集,条纹数量为23×2+1条;D为1 m和1.5 m时,条纹数量分别为11×2+1条,1.5 m时的7×2+1条;而D为2 m时,只能观察到5×2+1条.
2.3d取不同值在较小范围内观察的情况
当D=1.5 m,d取不同值时,在较小观察范围内,屏幕上干涉明条纹的分布情况.
图4(a)~4(d)为D=1.5 m,d分别为0.02 mm,0.1 mm,1 mm和3 mm时,在屏幕上较小观察范围内的分布[图4(c)~4(d)中只显示了中央明纹及其左右各50级干涉明纹].由图4的模拟结果可知,当D为1.5,在观察屏上较小范围内,随着d增加,相邻级次明纹间距变窄.当d为0.02 mm时,在屏幕上较小观察范围内,只能观察到3条明纹(包括中央明纹及其左右±1级明纹);d=0.1 mm时,能观察到7×2+1条明纹(到第7级);而d=3 mm时,条纹间距小的已无法用肉眼分辨;当d大于3 mm,观察屏上的明纹会进一步聚集而变得更窄,此时,在观察屏上应只观察到一条亮线,无法观测到干涉现象.这与干涉理论是一致的,因为随着d的增加,当d大到一定程度时,两缝光源将不再满足相干光源条件,所以也就无法观察到干涉现象.

图4 D=1.5 m,d取不同值时,屏幕上较小观察范围内明纹分布
2.4入射波长值取不同在较小范围内观察的情况
当D=1.5 m,d=0.1 mm,入射波长分别为400 nm,500 nm,600 nm和700 nm时,在较小观察范围内,屏幕上干涉明条纹的分布情况.
图5(a)~5(d)为D=1.5 m,d=0.1 mm,波长分别为400 nm,500 nm,600 nm和700 nm时,在屏幕上较小观察范围内的分布.由图5可知,当D为1.5,d=0.1 mm时,在观察屏上较小范围内,随着波长增加,相邻级次明纹间距变大,观察到的条纹数量变少.当波长分别为400 nm,500 nm,600 nm和700 nm时,在屏幕上较小观察范围内,分别能观察到9×2+1=19条、7×2+1=15条、6×2+1=13条和5×2+1=11条明纹.
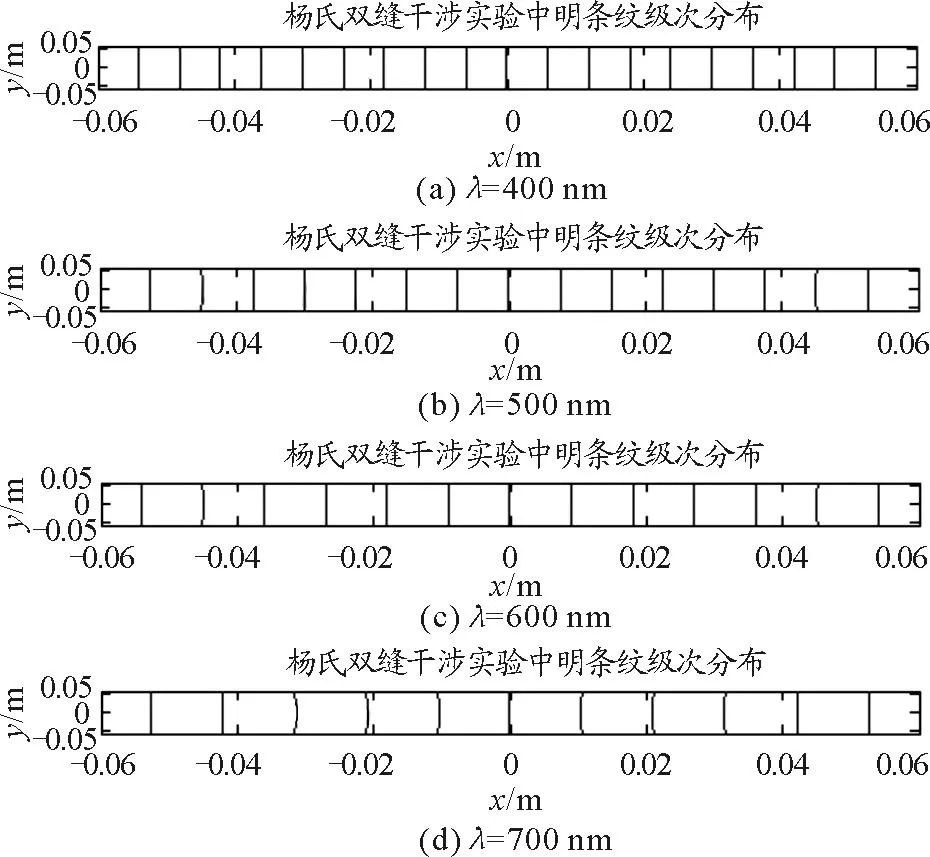
图5 D=1.5 m,d=0.1 mm,波长取不同值时,
由上述模拟结果可知:
(1)D取不同值时,在x轴右侧的观察屏上均能观察到干涉条纹,由于在两相干光波叠加区域内,处处都存在干涉的现象,称为不定域干涉,因而杨氏双缝干涉为非定域干涉.
(2)严格来说,观察屏上的条纹除中央明纹外为一系列双曲线,并非等间距直线.只是在较小观察范围内,才观察到平直的等间距干涉条纹,并且,随着D的增加,条纹间距变大.
(3)在同一D下,随着d增加,相邻级次明纹间距变窄,当d大到一定程度,肉眼将无法分辨干涉条纹.
(4)在D和d一定,入射波长不同时,随着入射波长增加,条纹间距变大,可观察到的条纹数量减小.
(5)D为m量级,d为0.1 mm量级,实验室可观察到清晰干涉条纹.
3结论
本文在未经任何理论近似的情况下,通过改变不同参数,模拟了观察屏上干涉明纹的分布,该模拟结果不但直观地展示了干涉条纹分布特点,有助于学生对干涉条纹分布规律的理解和掌握,而且可在一定程度上指导杨氏双缝干涉实验.另外,通过对比不同参数下的模拟结果,可引发学生对实验条件的关注,认识到实验条件的重要性.
参 考 文 献
1程守洙, 江之永.普通物理学.北京:高等教育出版社,1998.175~176
2张三慧.大学基础物理学.北京:清华大学出版社,2003.592~593
3马文蔚, 周雨青, 解希顺.物理学教程.北京:高等教育出版社,2006.185
4吴百诗. 大学物理.西安:西安交通大学出版社,2008.118~119
5金仲辉, 柴丽娜.大学基础物理学.北京:科学出版社,2010.260
Theoretical Simulation on Young′s Double-slit Interference Pattern
He KunnaHan PingZhu ShiqiuJin Zhonghui
(College of Science,China Agricultural University,Beijing100083)
Abstract:The paper theoretically simulated the fringe pattern on the screen in Young′s double-slit interference experiment in case that the theoretical analysis is not approximated. The simulation result is not only helpful for students to master the interference fringes in an all-round way, but also helpful for students to understand the importance of the experimental conditions.
Key words:double-slit interference;optical path difference;simulation
(收稿日期:2015-11-26)
作者简介:何坤娜韩 萍朱世秋金仲辉*何坤娜(1976-),女,博士,讲师,主要从事大学物理的教学工作以及新型激光器件与技术等方面的研究.
( 中国农业大学理学院应用物理系北京100083)

