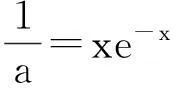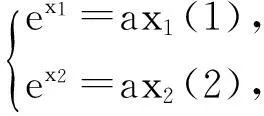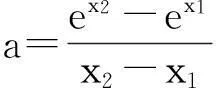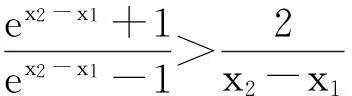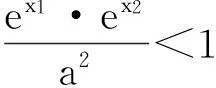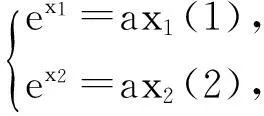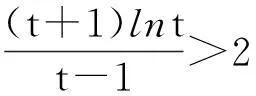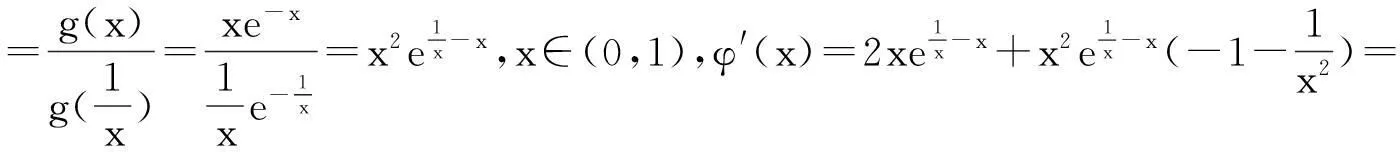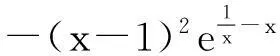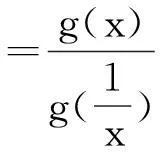一道高考模拟试题的多视角剖析
一道高考模拟试题的多视角剖析
四川省成都市石室中学(610010)苏文玉
以函数导数为背景,对函数的单调性,函数的零点进行分析,并对零点的分布,零点的大小进行判断、证明的题目在各地的高考试题及模拟题中经常出现,此类题能较好考察学生函数中的分析能力,函数与方程、函数与不等式以及构造函数解决问题的能力.并且此类题目中切入点比较多,思维开阔.例如我校在近期月考中选择题压轴题第12题就是这种情景,下面先看原题及解法.
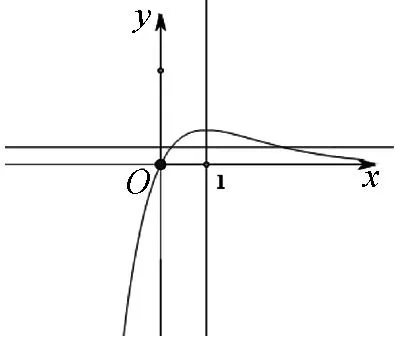
题目已知x1,x2是函数f(x)=ex-ax的两个零点,且x1 (A)a>e(B)x1+x2>2(C)x1x2>1 (D)函数有极小值点x0,x1+x2<2x0 解法1:数形结合视角. 就选填题来说,先用特殊分析的方式选出正确的选项. 如图1,当y=k与y=xe-x有两个交点时,令k→0,由图知x1+x2>2,B对.同样,从图形可知当k比较小时,x1比较接近0,而x2为一个正数,此时有 图1 x1x2<1,故C错.又易得f(x)的极小值点x0=lna.∵ex1=ax1,ex2=ax2⟹ex1+x2=a2x1x2 评析:解法1利用函数与方程的思想,将函数零点转化为两个函数交点的问题,并利用数形结合,用极限的思想选出了正确答案.作为选填题来说,是比较有效的一种方法,但不具有严谨性.但从数学思考的角度来说,这正是我们平时遇到这类探究型压轴题的思维模式,先利用特殊方法(特殊点、特殊值、图形等)得到正确的结果,再利用严密的数学理论证明结论.体现了“大胆假设、小心求证”的思维模式,下面就从多个角度来证明x1+x2>2和x1x2<1这两个结论. 解法2:消元视角一. 评析:本解法从消元的角度,消掉元a,得到一个关于x1,x2的多元不等式证明,利用换元的思想,将多元不等式证明变为了单元不等式,并通过构造函数证明了相应不等式.值得读者思考的是,为什么消元时要用两式相减来消去a,而不直接消元,这是因为为了使得欲证明的不等式具有对称性.同时对于本题双参不等式的证明,也可采取主元思想来证明,这个留给读者去完成. 解法3:消元视角二. 解法2和解法3都从消元的角度来切入这类多元问题,这种思想在高考中也经常出现,比如下面两道高考题留给读者练习: (Ⅰ)讨论f(x)在区间(0,+∞)上的单调性; (Ⅱ)若f(x)存在两个极值点x1,x2,且f(x1)+f(x2)>0,求a的取值范围. (2014年高考天津卷理科第20题)已知函数f(x)=x-aex(a∈R),x∈R,已知函数y=f(x)有两个零点x1,x2,且x1 (Ⅰ)求a的取值范围; (Ⅲ)证明:x1+x2随着a的减小而增大. 解法4:从极值点偏移视角. 由解法1数形结合可知,之所以出现这样的不等关系,本质是因为解法1中函数g(x)=xe-x在(0,1)单增,在(1,+∞)单减,但图像并不关于x=1对称,在(0,1)单增速度快于在(1,+∞)单减速度,所以产生不等式x1+x2>2,x1x2<1.我们经常称此为极值点偏移或类对称.下面就用对称变换的角度,通过构造相应函数来证明上述不等式. (ⅰ)先证x1+x2>2.令φ(x)=g(x)-g(2-x)=xe-x-(2-x)ex-2,x∈(0,1).φ′(x)=e-x-xe-x+ex-2-(2-x)ex-2=(1-x)e-x+(x-1)ex-2=(1-x)(e-x-ex-2),∵x∈(0,1),∴-x>x-2,∴e-x>ex-2,∴φ′(x)>0.∴φ(x)在区间(0,1)上单增,∴φ(x)<φ(1)=0.∵g(x2)=g(x1) 同样给出两道高考题留给读者练习. (2010年高考天津卷理科第21题)已知函数f(x)=xe-x(x∈R). (Ⅰ)求函数f(x)的单调区间和极值; (Ⅱ)已知函数y=g(x)的图像与函数y=f(x)的图像关于直线x=1对称,证明当x>1时,f(x)>g(x); (Ⅲ)如果x1≠x2,且f(x1)=f(x2),证明x1+x2>2. (2011年高考辽宁卷理科第21题)已知函数f(x)=lnx-ax2+(2-a)x. (Ⅰ)讨论f(x)的单调性; (Ⅲ)若函数y=f(x)的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,证明:f′(x0)<0. 其实,解决此类根的分布的不同方法,实质上都是把两个变元的不等式转化为一元问题求解,途径都是构造函数.所以解法的本质就是构造函数.文[1]中邢老师的解法是根据对称性构造函数,而文[2]中赖老师转化为对数平均的解法是捆绑构造函数.本文则通过一道调研试题的多角度思考,给出了四种不同的解题视角,不仅体现出不同的思维层次,并且蕴含了深刻的数学思想方法,也体现了数学研究中的从特殊到一般的探究过程,在数学的教育教学中,通过一题多思、一题多解、一题多讲,可以巩固学生知识,训练学生思维,开拓学生视野.利用多角度去看一道题,强化思维的连贯性、知识的衔接,能够全面利用所学知识解决一些实际问题,对培养学生对知识的灵活应用有着重要的帮助. 参考文献 [1]刑友宝.极值点偏移问题的处理策略[J].中学数学教学参考.上旬,2014(7):19-22. [2]赖淑明.从对数平均谈极值点偏移问题[J].中学数学研究(广州).上旬,2015(4):31-32.