2015年国际数学奥林匹克不等式问题及解答集粹
2016-04-06 02:20:50王文江
中学数学研究(江西) 2016年2期
2015年国际数学奥林匹克不等式问题及解答集粹
南昌大学附属中学(330047)王文江
笔者从2015年世界各国数学奥林匹克近百道不等式题中精心挑选出特征鲜明风格迥异的好题若干,并配上十分漂亮雅致的解答,以飨老师与同学.
例1(2015年罗马尼亚数学奥林匹克) 已知a,b,c是满足a>bc2,b>ca2,c>ab2的正数,求abc(a-bc2)(b-ca2)(c-ab2)的最大值.
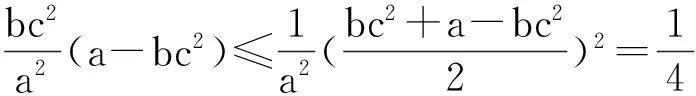
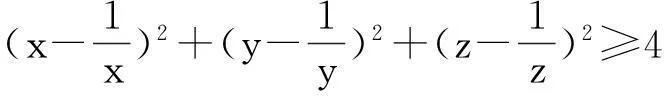
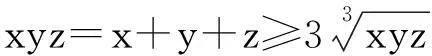
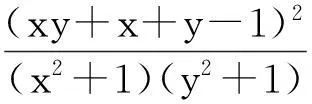
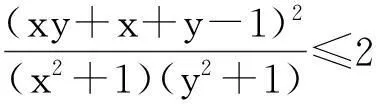
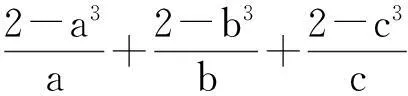
解:∵(ab-bc)2+(bc-ac)2+(ac-ab)2≥0,∴(bc+ca+ab)2≥3abc(a+b+c),
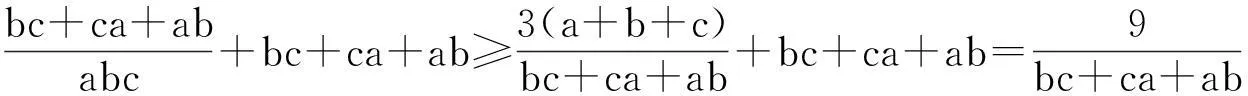
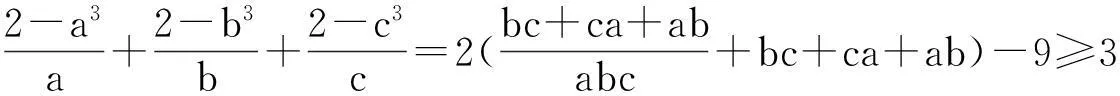
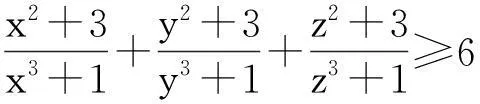
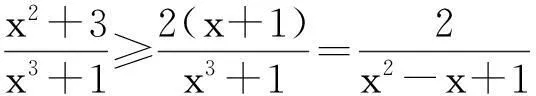
(-1 例8(2015年韩国数学奥林匹克) 已知a,b,c,x,y是满足a2+b2+c2=x2+y2=1的实数.求(ax+by)2+(bx+cy)2的最大值. 例9(2015年韩国数学奥林匹克)已知a,b,c,x,y是满足a2+b2+c2+x2+y2=1的实数.求(ax+by)2+(bx+cy)2的最大值. 解:∵(ax+by)2+(bx+cy)2≤(ax+by)2+(bx+cy)2+(cx-ay)2=(x2+y2)(a2+b2+c2)+2(ab+bc-ca)xy(*)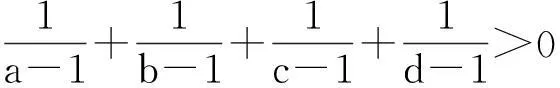
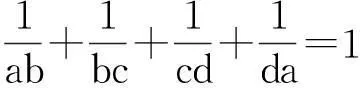
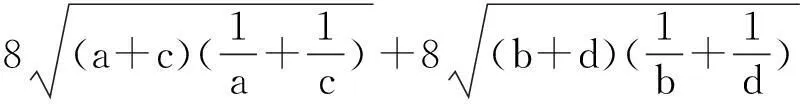
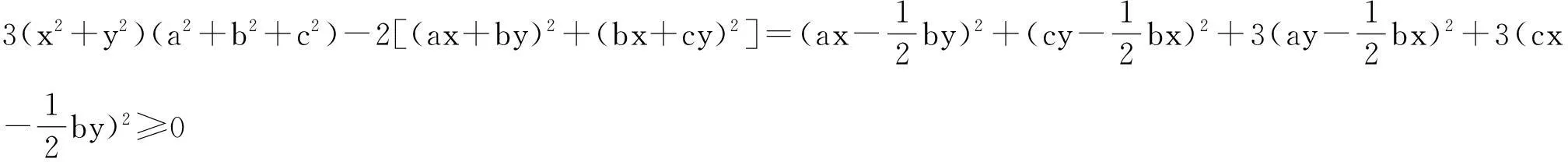
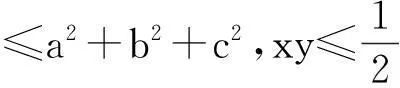
猜你喜欢
南昌大学学报(医学版)(2022年3期)2022-07-20 02:17:52
南昌大学学报(医学版)(2022年2期)2022-05-30 07:22:54
中学生数理化·高一版(2021年12期)2022-01-17 09:31:30
中学生数理化·高一版(2021年12期)2021-09-05 14:26:48
江苏教育(2021年54期)2021-08-31 10:12:32
中小学校长(2021年7期)2021-08-21 06:49:56
南昌大学学报(医学版)(2021年3期)2021-07-21 13:48:44
南昌大学学报(医学版)(2020年3期)2020-08-17 02:27:28
小学生作文(低年级适用)(2019年10期)2019-10-28 06:46:26
新世纪智能(语文备考)(2018年11期)2018-12-29 12:31:00

