能否用一元二次方程根的分布判定直线与圆的位置关系
2016-04-06 02:20雷雨田
中学数学研究(江西) 2016年2期
能否用一元二次方程根的分布判定直线与圆的位置关系
湖北省监利中学(433300)雷雨田
1提出问题
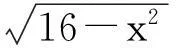
一道传统题,常见解法有数形结合,三角代换和导数法,当然也容易想到转化为一元二次方程来考虑.
思路2题意转化为f(x)=0在x∈[-4,4]上有两个不等实根,于是


以上是解答时常见的转化为一元二次方程的两种思路,特别是思路2,貌似考虑了x∈[-4,4]的限制,为何与思路1的结果还是一模一样,是巧合?还是利用一元二次方程根的分布方法判定直线与圆的位置关系根本无效?
联想到学习《数学》必修2(人民教育出版社)P127页时的困惑:
P127页第4.2.1节例1已知直线l:3x+y-6=0和圆心为C的圆x2+y2-2y-4=0,判断直线l与圆的位置关系.
解:由直线与圆的方程,得
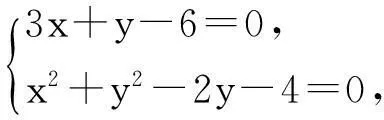
在这个例题的学习时,就有这样的困惑:由圆C:x2+(y-1)2=5知,问题应当还要加上x∈

2分析问题
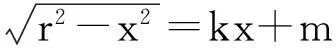
思路2考虑f(x)=(k2+1)x2+2kmx+m2-r2=0在x∈[-r,r]上有两个不等实数根:
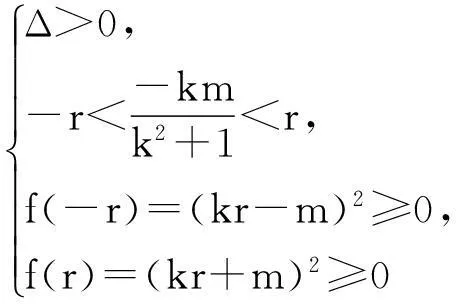
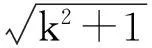
看来真不是巧合,直线与圆的位置关系判定,不需要考虑x∈[-r,r]的限定,不需要用一元二次方程根的分布,只要△>0,直线与圆相交;△=0直线与圆相切;△<0直线与圆相离.
这两个解法正好解答了前面学习数学《必修》2教材P127页的困惑.
那么是否说例题也不需要用根的分布方法来解决了吗?
再回到原来的例题:
3解决问题
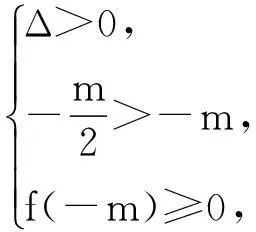

综上所述,解法一回答了怎样利用一元二次方程根的分布解直线与圆,直线与半圆的交点个数的问题.
而解法二、三、四的实质都是将方程根的个数问题利用数形结合转化为两个图像的交点个数问题,其中解法二在处理直线与半圆的交点时更常见.
4高考链接
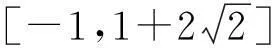


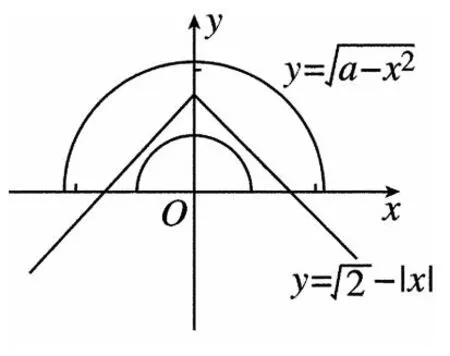
图1
猜你喜欢
中学生数理化·中考版(2022年9期)2022-10-25
中学生数理化·中考版(2021年9期)2021-11-20
孩子(2021年1期)2021-01-27
学生导报·东方少年(2019年7期)2019-06-11
小学生学习指导(高年级)(2018年10期)2018-10-10
中等数学(2018年6期)2018-08-02
中学生数理化·中考版(2017年3期)2017-11-09
初中生世界·九年级(2017年9期)2017-10-13
数学学习与研究(2017年11期)2017-06-20
青年时代(2017年3期)2017-02-17

