几道圆锥曲线高考试题的背景探究与拓广*
几道圆锥曲线高考试题的背景探究与拓广*
广东省广州市第六中学(510300)吴林
纵观近几年各地高考题,不少试卷都会选择用圆锥曲线相关内容命制压轴题,通过对高考题的研究,笔者发现不少高考题都是以课本的习题为素材,通过变形、延伸和拓展来命制的.课本是数学知识和数学思想方法的载体,又是教学的依据,理应成为高考试题的源头,因此我们平时教学中应该加强对典型习题的探究,教会学生识别相关模型,理解问题的本质,达到通过做几道题,解决一类题的目的.本文对此作出探讨,请广大同仁批评指正.
一、三道高考题
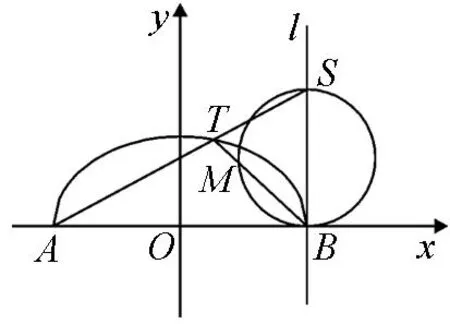
图1
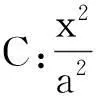
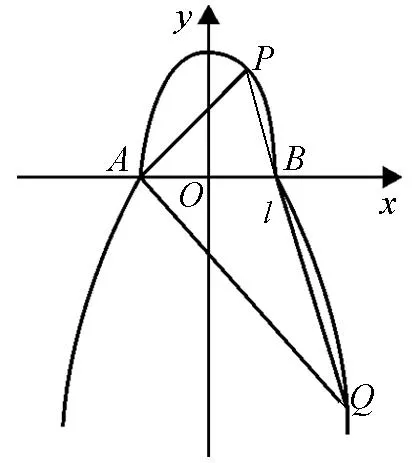
图2
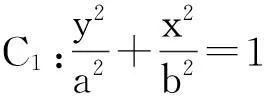
(1)求a,b的值;(答案:2,1)
(2)过点B的直线l与C1,C2分别交于P,Q(均异于点A,B),若AP⊥AQ,求直线l的方程.
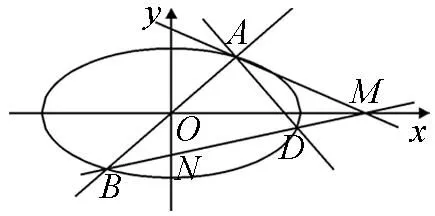
图3
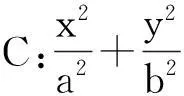
(Ⅱ)如图3,过原点的直线与椭圆C交于A,B两点(A,B不是椭圆C的顶点).点D在椭圆C上,且AD⊥AB,直线BD与x轴、y轴分别交于M,N两点.
(i)设直线BD,AM的斜率分别为k1,k2,证明存在常数λ使得k1=λk2,并求出λ的值;(ii)略.
二、背景的探究
上述三道高考试题都涉及到“椭圆上任意一点与椭圆上关于原点对称两点的连线斜率之积”的问题,笔者认为这三道题是以课本(人教A版数学《选修2-1》,下同)P41的例题3为基础素材编制而成的.
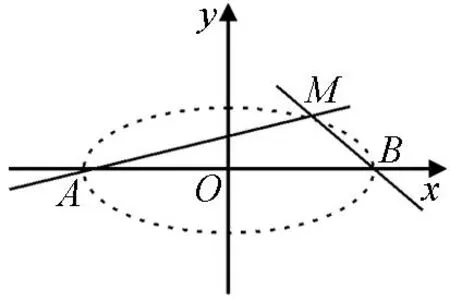
图4
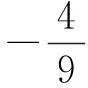
对此题进行拓展延伸,我们不难得到以下结论(相关证明略):
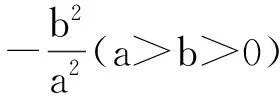
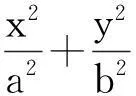
利用结论2,我们很容易就可以解答题1:
利用此结论,易得题2和题3的解答:
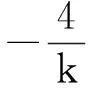
三、问题的拓广
将上述问题从椭圆拓展延伸到双曲线中,可以得到类似的性质:
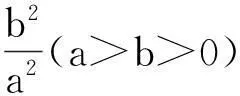
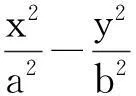
应用此结论,不难解出以下两道高考试题:
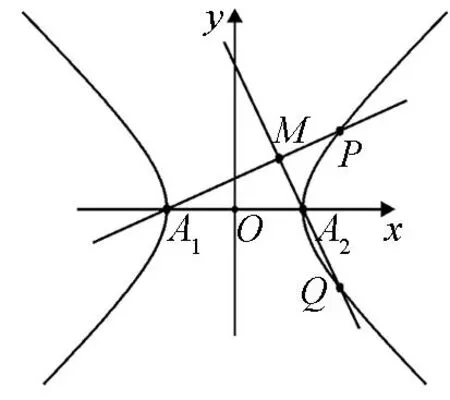
图5
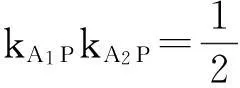
图6
根据题4,同理解出此题:点M的轨迹是双曲线(在第三象限的部分).
在平时的教学中,我们多在这类典型例题上下功夫,让学生识别图形、理解问题的本质,这样学生在新的情景下,才能将所学方法应用到新问题中,减少运算量和思维量.
事实上,因为圆、椭圆和双曲线都是有中心的二次曲线,所以我们对上述问题进一步拓展延伸,可以得到如下结论[1]:
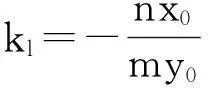
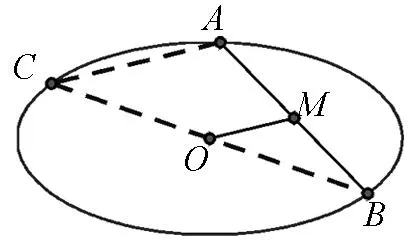
图7
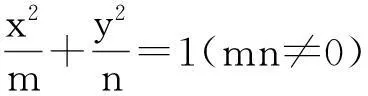
教材中有不少题目,如果我们对其进行挖掘、延伸、转化和拓广,就会得到一些综合性强,符合高考命题精神的新命题,这样不仅能激发学生的兴趣,而且符合高考题源于课本、高于课本的命题思想,同时能引导学生跳出“题海”,回归课本,重视教材.
这种寻找背景、探究拓展的过程,令人兴趣盎然,也是学好数学的正确途径.数学教学的本质是学生在教师的引导下能动地建构数学认知结构,使自己得到全面发展的过程[2].对问题的探究拓广是习题教学中常见的有效手段,在教学中,我们应该通过启发、鼓励学生自己发现问题的规律、内在的联系、识别图形模式、掌握代数运算中反映的本质问题,使学生真正地将方法内化,将问题形成串,结成网,以促进学生知识的系统化、结构化、综合化和应用化,从而真正提高学生的数学能力与数学素养.
参考文献
[1]陈国伟,蔡小雄.改进:为了追求问题本质的习题教学[J].中学数学教学参考.上旬,2014(11),51-52.
[2]何小亚.数学教与学的心理学[M].华南理工大学出版社.
*本文是广东省教育科研“十二五”规划2013年度研究一般项目“在校本教研中开展数学考试命题及评价的研究”的研究成果,课题批号:2013YQJK055.

