以拐点偏移为背景的函数导数试题命制*——兼谈试题处理策略
以拐点偏移为背景的函数导数试题命制*
——兼谈试题处理策略
厦门大学附属实验中学(363123)田富德陈小燕
文[1]对极值点偏移问题提出了巧妙的处理策略,轻松解决了一类高考题、省市质检题的压轴题,体现了教学中注重通性通法的解题策略,这是文[1]的一大亮点.笔者将分析法解题思想渗透于本文的自编试题之中.受到文[1]的启发,极值点偏移问题的处理策略基于轴对称思想进行构造差函数,进而逆用单调性解题.那么我们是否可以基于中心对称思想进行构造差函数处理新的一类试题呢?本文尝试以拐点偏移函数为背景命制新的一类函数导数试题,并给出相应的解题策略.
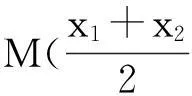
1背景函数
1.1以常见不等式“ex≥x+1”为背景命制试题


(Ⅰ)求函数f′(x)的单调区间和极值;
(Ⅱ)已知函数y=g(x)的图像与函数y=f(x)的图像关于原点对称,证明:当x>0时,f(x)>g(x);
(Ⅲ)如果x1≠x2,且f(x1)+f(x2)=0,证明:x1+x2<0.
解:(Ⅰ)f′(x)在(-∞,0)上单调递减;在(0,+∞)上单调递增.f′(0)=0为f′(x)极小值,无极大值.
(Ⅲ)由(Ⅰ)知,f′(x)≥0,即f(x)在R上单调递增,且f(0)=0.因为x1≠x2,不妨设x1
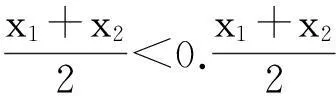
1.2以常见不等式“lnx≤x-1”为背景命制试题
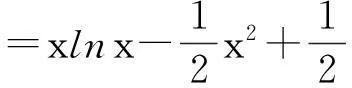
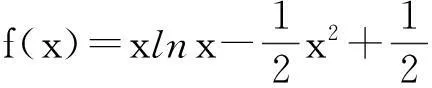
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)证明:当x1≠x2,且f(x1)+f(x2)=0时,x1+x2>2.
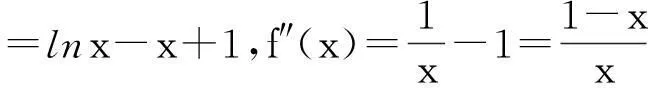
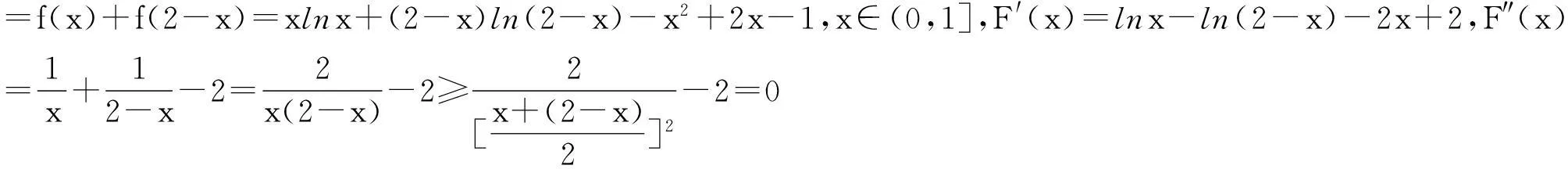
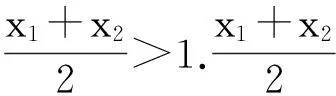
例3设函数f(x)=x2+2lnx-4x,函数f′(x)为f(x)的导函数.
(Ⅰ)求函数f(x)在x=2处的切线方程;
(Ⅱ)证明:当x1≠x2,且f(x1)+f(x2)=-6时,f′(x1+x2)>1.
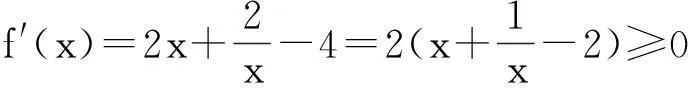
令F(x)=f(x)+f(2-x)=x2+2lnx-4x+(2-x)2+2ln(2-x)-4(2-x),x∈[1,+∞),化简得F(x)=2[x2-2x-2+lnx+ln(2-x)].

所以(*)式成立,即有f′(x1+x2)>1成立.
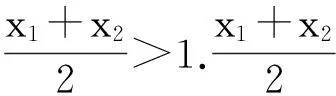

(Ⅱ)设A(x1,f(x1)),B(x2,f(x2))是f(x)的图像上不同的两点,且满足f(x1)+f(x2)=0,线段AB的中点横坐标为x0,证明:ax0>1.


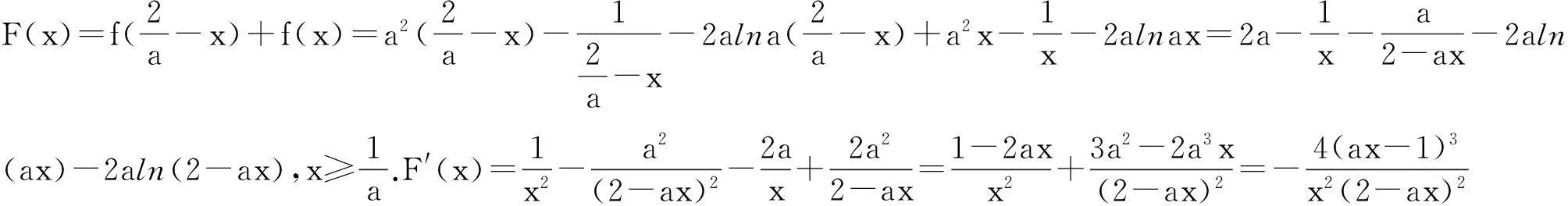
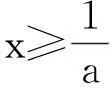
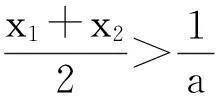
2命题策略
本文以拐点偏移问题为背景命制一类函数导数的试题,根据拐点的定义,我们要保证函数二阶导有零点,同时还要求一阶导恒大于等于零(或小于等于零),以保证原函数具有单调性.故我们首先由熟知的不等式构造相应的导函数,进而求出原函数,再对函数上下平移或左右平移,来调整拐点的位置,以控制试题的难度.
弄清问题的本质,解题则势如破竹,而对原问题进行改编、新编也易如反掌.中学数学教师要有良好的解题基本功,才能更好的服务课堂教学.坚持做题,是命题的基础,对试题命题研究,可以站在解题的至高点上,得出解题的一般规律,以促进数学特长生的培养.解题与命题和数学特长生培养相长,中学数学教师应重视解题研究和命题研究.
3解题策略
无论是极值点偏移问题,还是拐点偏移问题,均是已知f(x1)与f(x2)关系,证明与x1,x2有关的不等式.其本质上是证明双变量不等式问题,而先由条件消元再构造函数是解决双变量问题的有效途径之一.在条件为双变量的函数方程时,要由条件将变量x1用另一个变量x2表示几乎不可能,故将所证不等式逆用单调性转化为与f(x1)、f(x2)有关的不等式是一个有效策略,再结合条件代入消元,构造函数即可.
文[1]对极值点偏移问题,给出了巧妙的解题策略,并归纳出规范的解题策略,给出了严格的解题步骤,给学生解题指明了方向.
在高考创新试题层出不穷的大环境下,学生首先要掌握基本的知识方法和解题策略,对新题、难题的突破,笔者更支持在掌握双基的前提下,淡化特殊技巧、重视思想方法、去模式化的解题策略,以不变应万变,培养学生分析问题、解决问题的能力.笔者在本文自编例题的最后一问的解答均保留了分析法的解题规范,个人认为这样可以让解法显得更流畅一些,也更符合学生的认知规律.分析法解题,可以有效建立起问题已知与求解之间的桥梁,利用熟知的知识方法去解决各类未知的创新试题,也是培养学生解题思维的广阔性、逆向性等的重要途径之一.分析法解题,体现了中学数学中的转化与化归思想.
4你来试试
(Ⅰ)探求函数g(x)=f(x)+m-x2在区间(0,+∞)上零点的个数;
(Ⅱ)证明:当x1≠x2,且f(x1)+f(x2)=0时,x1+x2>2.
参考文献
[1]邢友宝.极值点偏移问题的处理策略[J].中学数学教学参考.上旬,2014(7):19-22.
*本文系2015年度漳州市基础教育课程教学研究立项课题《高中数学解题教学现状与优化》阶段性研究成果.

