寻根问源 多方探究——一道数学竞赛题的探究历程
寻根问源多方探究
——一道数学竞赛题的探究历程
江苏省常熟市浒浦高级中学(215512)殷伟康吴进
1问题提出
2(b-a)≤cosπa-cosπb.(2013年全国高中数学联赛江苏赛区初赛试题第13题)
此题虽然是一道解答题,但题干精练简洁,个性鲜明,内涵丰富,看似普通,却越探索越感到有“味道”,越能体会到命题者的匠心独具,不亏为一道魅力无穷的好题.笔者试从探索其解法入手,逐步揭开它“神秘”的面纱,并给出它的奇妙多解.
2.常规方法
对于学过导数的学生,此题的入手并不难,根据所给式子的结构特征,通过联想,可以构造函数f(x)=2x+cosπx ,利用导数研究函数的单调性进行证明.
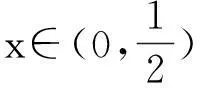
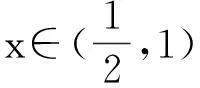
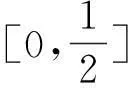
这个证法是参考答案给出的,笔者试从学生实际认知和思维能力角度出发来思考问题,探究其解法.上述证明过程中的二阶求导对部分学生来说不易理解,能否进一步改进证法使它能更适合一般学生的“口味”.
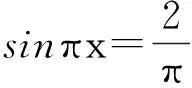
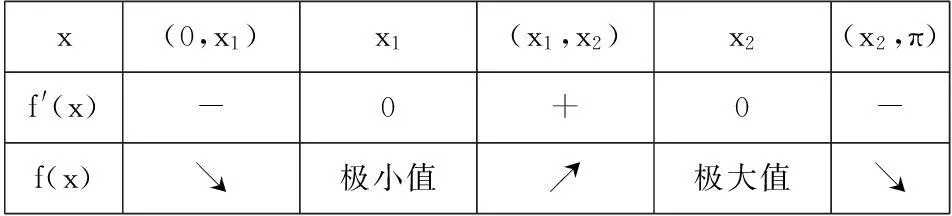
x(0,x1)x1(x1,x2)x2(x2,π)f'(x)-0+0-f(x)↘极小值↗极大值↘
下面同证法一.
通过对原解题方法的改进,使其更贴近学生的实际思维水平,这是因为二阶求导在中学阶段并没有给出相应的实际意义,而且接触得很少,所以一般不直接去涉及这方面内容.
3三角方法
笔者在不经意间想到,上述解题方法涉及到导数知识,但在我市有不少高一学生也参加了这次高中数学联赛,他们仅学过了苏教版《必修一》和《必修四》,掌握的仅是函数、三角、向量等知识,那么他们应如何入手求解这个问题呢?笔者根据问题结论的外表形态与结构,联想相关图形(余弦函数图像),试从三角函数图像角度入手,运用数形结合进行求解.
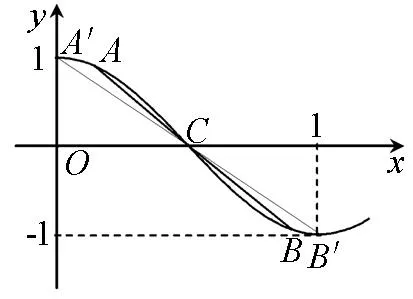
图1
①+②有cosπa-cosπb≥2(b-a)成立,即得证.
证法三:直接看y=cosπx,x∈[0,1]的图像(如图2),如图过点A、B分别作x轴、y轴的垂线,两垂线相交于点M,利用证法二设点A、B,则M(a,cosπb),记M′为(0,-1),则|AM|=cosπa-cosπb,|BM|=b-a.考察y=cosπx,x∈[0,1]的图像,根据其凹凸性知∠ABM≥∠A′B′M′, ∴tan∠ABM≥tan∠A′B′M′, 即
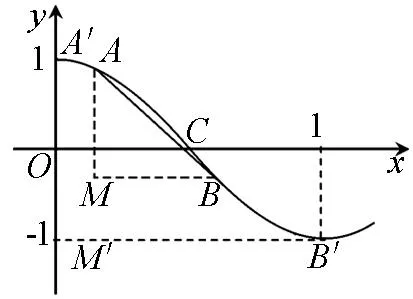
图2
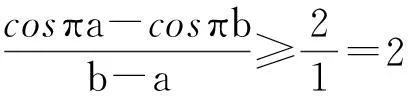
我们知道,余弦函数图像是可由正弦函数图像变换得来的,能否利用正弦函数来处理呢?
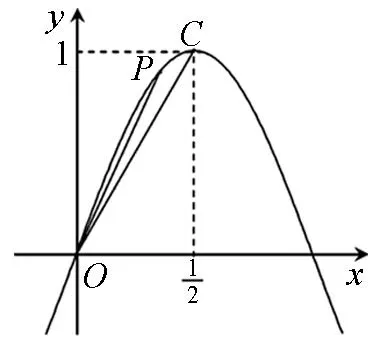
图3
此法让人感到:图像清晰,方法简明,一气呵成,妙解也!
此结论证法较多,下面用导数方法证之:
4解题反思
章建跃先生认为,从数学角度衡量,“好题”应具有以下“品质”:与重要的数学概念和性质相关,体现基础知识的联系性,解题方法自然、多样,具有自我生长的能力等;从培养思维能力的角度,则应有:问题是自然的,对学生的智力有适度的挑战性,题意明确、不纠缠于细枝末节,表述形式简洁、流畅、好懂等.按此“标准”,上述竞赛题就是一个“好题”,问题正好贴近学生思维的最近发展区,既有解决的可能性,又有挑战性,它不仅适合不同层次学生的学习和探究,而且还可以在追根溯源的过程中,加以引伸与推广.
反思解题过程,分析问题特征、数学关系,重新审视探究过程(上述四种证法),不难发现原问题的实质就是三角函数的凹凸性. 函数f(x)的凹凸性的知识在高中教材中有其踪迹,如苏教版《数学·必修1》第二章第二节“指数函数”第55页习题“探究·拓展”第12题,第二章第三节“对数函数”第71页习题“探究·拓展”第12题.若能以这两个“探究·拓展”习题作为探究问题,引导学生开展有效的探活动,在探究活动中让学生自行发现数学规律,可以使学生深切体验到新知识的产生、证明和应用过程,积累数学基本活动经验,领悟其中所蕴含的数学思想方法,发展数学能力.教师应抓住时机,及时对这两个习题进行适度拓展与延伸,诱导学生作进一步的探究,还可以适时引进判断函数f(x)的凹凸性的简洁方法(二阶求导),有利于学生加深对函数f(x)的凹凸性的理解和运用,把握函数f(x)的凹凸性的本质规律,促进学生思维由具体向抽象推进.这样的教学才是有效的,使学生遇到上述相似问题就会产生有效联想,通过类比,进行合理求解.否则,不仅良好的教学素材会被轻易地“滑过”,而且很难想象学生会联想到这一方面知识进行有效思维.
数学思想是对数学知识的本质认识,是从具体的数学内容和数学认识中提炼而得出的数学观点.上面四种证法中的后三种证法均是运用数形结合思想进行求解,即由问题的结论特征,联想到余弦函数或正弦函数图像,进而发现数与形之间的内在联系,从而使代数问题几何化,使问题得到解决.笔者从“形”的角度进行思考,抓住题目中所给的式子,观察其结构特征,从它们的几何意义入手.根据问题所给信息,通过数形联想,挖掘其几何背景,进行图形表征,利用数形结合思想,得到新颖、优美、简洁的解题方法.

