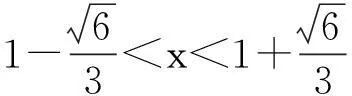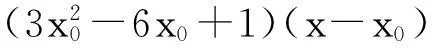例谈切线法解导数压轴题



例谈切线法解导数压轴题

山东省泰安市宁阳一中(271400)张显文

切线是曲线割线的极限位置，是曲线的局部几何性质，也可以将切线理解为在曲线局部直线与曲线由相离到接近的极限位置.因其位置的特殊性，在研究直线与曲线位置关系时充分利用切线性质对于为减少解题时的思维量与运算量大有裨益.笔者结合几例导数压轴题具体谈一下切线的应用.

(Ⅰ)当k≤0时，求函数f(x)的单调区间；

(Ⅱ)若函数f(x)在(0,2)内存在两个极值点，求k的取值范围.

解析：(Ⅰ)略；

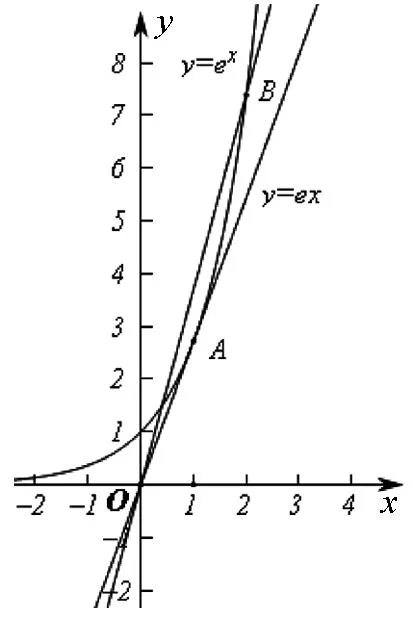
图1

所以“f(x)在(0,2)内存在两个极值点”等价于“ex-kx=0在(0,2)内有两个不等实根”，等价于“曲线y=ex与直线y=kx在(0,2)内有两个交点”.

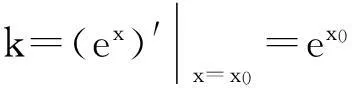
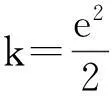
例2(2015泰安市二模21)已知函数f(x)=xlnx+ax(a∈R).

(Ⅰ)若函数f(x)在区间[e2,+∞)上为增函数，求a的取值范围；

(Ⅱ)若对任意x∈(1,+∞)，f(x)>k(x-1)+ax-x恒成立，求正整数k的值.

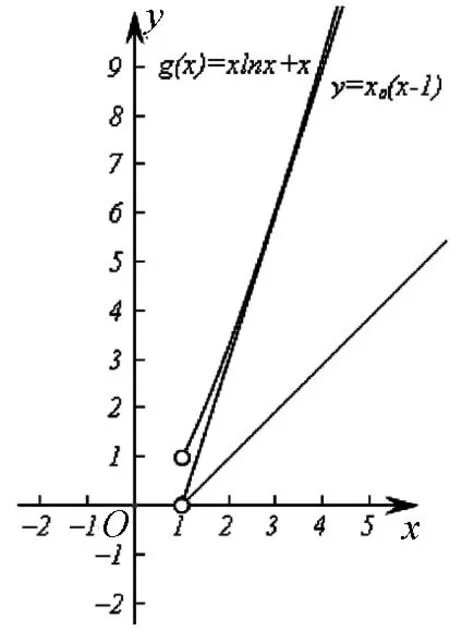
图2

解析：(Ⅰ)略；

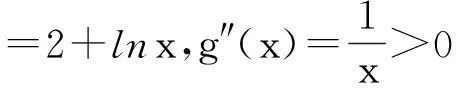
例3(2013年新课标Ⅱ理21)已知函数f(x)=ex-ln(x+m).

(Ⅰ)设x=0是f(x)的极值点，求m,并讨论f(x)的单调性；

(Ⅱ)当m≤2时，证明f(x)>0.

解析：(Ⅰ)略;

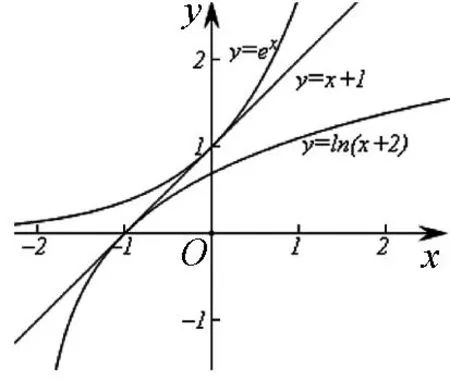
图3

(Ⅱ)因为m≤2，所以x+m≤x+2,ln(x+m)≤ln(x+2).因为函数y=ln(x+2)的图像上凸，如图3，在点(-1,0)处的切线方程为y=x+1，所以ln(x+2)≤x+1(“x=-1”时取等号).又因为函数y=ex的图像下凸，在点(0,1)的切线方程为y=x+1，所以ex≥x+1(“x=0”时取等号).所以ex≥x+1≥ln(x+2)，因为等号不能同时取，所以ex>ln(x+2)，于是得ex>ln(x+m)，所以f(x)=ex-ln(x+m)>0，不等式得证.

例4(2014年新课标Ⅱ文21)已知函数f(x)=x3-3x2+ax+2，曲线y=f(x)在点(0,2)处的切线与x轴交点的横坐标为-2.

(Ⅰ)求a；

(Ⅱ)证明：当k<1时，曲线y=f(x)与直线y=kx-2只有一个交点.

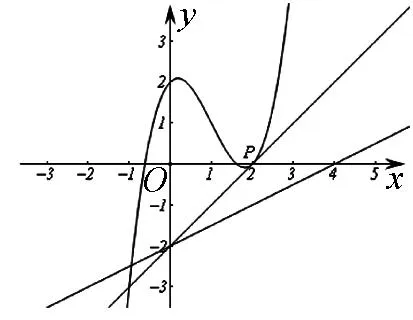
图4

解析：(Ⅰ)a=1；