随机变量特征函数的求法研究
蒋同斌
(淮阴工学院 数理学院,江苏 淮安 223003)
随机变量特征函数的求法研究
蒋同斌
(淮阴工学院 数理学院,江苏 淮安 223003)
摘要:分布函数由其特征函数唯一决定, 判断函数为特征函数的条件,成为特征函数的基本要求、基本类型及其具体的确定,利用特征函数的定义积分变换和积分方法等说明特征函数的求解方法,讨论特征函数在数学通信保险数据查询等生产实际中的具体应用。
关键词:特征函数;分布函数;求解方法;实际应用
概率论中,随机变量的数学期望和方差只能粗略地反映其分布函数的性质,而分布函数由其特征函数唯一决定[1]。

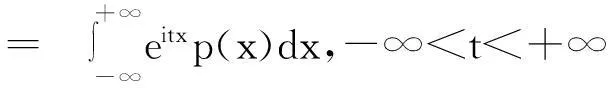
从以下方面讨论随机变量特征函数的求解方法。
1 判断函数为特征函数的条件与实例
1.1判断函数为特征函数的条件
辛钦一渡赫纳尔定理[2]: 函数f(t)是特征函数的充要条件是
(1)函数f(t)是非负定性的;(2)f(t)连续;(3)f(0)=1 。
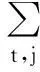
1.2实例


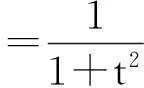
2特征函数的求解方法
2.1根据特征函数的定义求解
例1设随机变量X的分布如下(见表1),试求X的特征函数。

表1 随机变量X的分布表
解:已知X的分布列为pk=P(X=xk),k=0,1,2,3,所以X的特征函数为:
=0.4+0.3eit+0.2ei2t+0.1ei3t
例2设离散随机变量X服从几何分布P(X=k)=(1-p)k-1p,k=1,2,…求的特征函数。
解:已知X的分布列为P(X=k)=(1-p)k-1p,k=1,2,…所以X的特征函数为
2.2已知分布函数求解特征函数

2.3常用分布的密度函数求解特征函数
(1)求均匀分布的特征函数
(2)求指数分布的特征函数
所以特征函数为
f(t)=∫0+∞eitxλe-λxdx=λ{∫0+∞cos(tx)eλxdx+i∫0+∞sin(tx)e-λxdx}
(3)求标准正态分布的特征函数
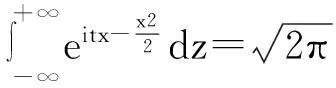
2.4利用独立随机变量和的特征函数为特征函数的积来求解和的特征函数

2.5用高效积分法求解特征函数
随机变量的概率密度函数与特征函数可以表示为一个Fourier变换对[3],定义为
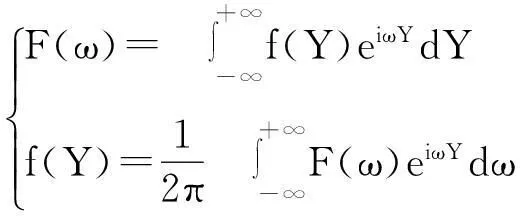
利用Fourier的位移性质求(1)中的F(ω)有
(2)
对f(Y)进行坐标平移t0,f(Y)→f(Y-t0),于是式(2)变为:
(3)
式(2)表明,F(ω)是另一函数Y'=e-iωY的均值。因为Y=Y(V)⟹Y'=Y'(V),所以式(2)又可写作
F(ω)=E{Y'(V)}=∫ΩY'(V)f(V)dV
(4)
Ω是积分区域,而式(4)的积分可以完全利用高效数值积分法来完成。另外假设随机变量x1,x2,…,xn服从正态分布且相互独立。那么由于x1,x2,…,xn是n个相互独立的正态分布随机变量,因此,它们的联合概率密度函数可以表示为
(5)
于是式(4)的积分可以写为
(6)
3特征函数单调性与迭代数列收敛性之间的关系
利用特征函数单调性判断迭代数列收敛性[4]并求其极限。
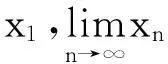
证明:对于任意的x1,有-1≤xn≤1(n=2,3,…),因此F(x)=x-f(x)=x-c·sinx是{xn}在区间[-1,1]上的特征函数。又当x∈[-1,1]时,F'(x)=1-c·cosx≥0(其中等号仅当c=1,x=0时成立),故F(x)和f(x)在[-1,1]单调增加,且F(0)=0。故由定理2知{xn}的极限存在且等于0。
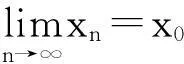
4二维随机变量的特征函数
二维随机变量特征函数的求法
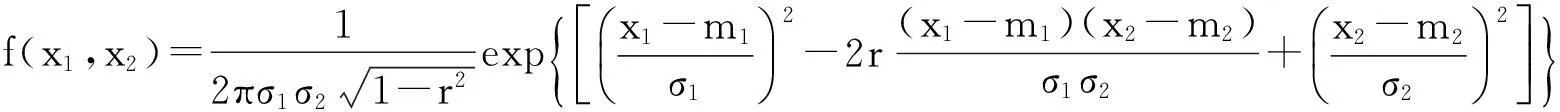
解:它的特征函数为
f(t1,t2)=∫-∞+∞∫-∞+∞ei(t1x1+t2x2)f(x1,x2)dx1dx2
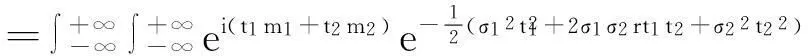
特别,当m1=m2=0,σ1=σ2=1时,即(ζ1,ζ2)~N(0,1;0,1;r),则
当η=αζ1+βζ2+r,(α、β、γ为实常数)时,η的特征函数为

5特征函数的应用
特征函数在许多领域中广泛应用,如在数学、无线通讯、数据库查询等方面,下面就其在数据库查询方面的应用作简要说明[5]。利用特征函数来改善系统效率,提高查询速度。从结构上讲,利用SQL内部基本数符和函数,特征函数可编写成数量表达式,具体编码依赖于各种语言内部特性以及涉及到的变量数据类型。目前已开发了处理各种数据类型的技术,在此简单介绍将特征函数限于数字类型实例。
特征函数一般的编码形式为1-abs(sign(A-B)),sign()和abs()是内部Sybase函数。abs()返回变量的绝对值;当变量为负数、零和正数时sign()分别返回-1、0、+1。
以下是特征函数的编码(不考虑空值情况):
δ[A=B]=1-abs(sign(A-B))δ[A δ[A<=B]=sign(1-sign(A-B))δ[A>B]=1-sign(1-sign(A-B)) δ[A>=B]=sign(1+sign(A-B)) 例如:对于表student(name,status,parincome,selfincome),它包括学生姓名、独立状况(1代表独立,0代表非独立)和两种收入(来自父母和自己的)。假设要生成表格(name,income),分别包括非独立学生和独立学生来自父母和自己的收入,传统的SQL方法如下: SELECT name,income=parincome*status+selfncome*(1-status) FROM students 而利用上述讨论的特征函数查询,语句如下: SELECT name, income=parincome*δ[status=1]+selfincome*δ[status=0] FROM students 传统的查询方法,如语句(1),一旦问题复杂化,即状态不仅是0或者1时,用公式不能直接表达出问题。例如条件不只一个时,如考虑属性“年龄”,我们利用特征函数编码的方法得到如下的查询语句: SELECT name, income=parincome*δ[status=1]δ[age<=19]+selfincome*sign(δ[status=0]+δ[age>23])+(parincome+selfincome/2.0)*(1-δ[status=1])*δ[age<=19]-sign(δ[status=0])*δ[age>23] FROM students 此查询过程是:学生在19岁或19岁以下且非独立的,结果返回parincome;学生独立或大于23岁的,结果返回selfincome;其它情况则返回算术平均值。传统的SQL解决条件查询问题需要多个SQL语句,对每个条件进行一次数据访问,最后通过UNION合成结果。而现在只用一个SQL语句,做一次数据访问,这种方法不仅节约了查询所需访问数据表的次数,节省时间,减轻计算机工作量。 6结论 随机变量特征函数的求法及应用,对于初学者来说是有难度的。傅里叶变换是一个有效工具,特征函数能够决定分布函数,并且具有好的性质,是研究概率分布的最好的方法,特别是研究随机变量序列的概率分布的极限问题起关健作用,论文的目的是利用积分变换和积分方法,结合具体实例进行分析说明,有利于我们更好地认识特征函数。论文首先用辛钦一渡赫纳尔定理给出了判断函数是否为特征函数,并运用几种不同的方法求解特征函数,使其在数学领域和其它方面得到了广泛的运用。 参考文献: [1] 程依明,濮晓龙.概率论与数理统计教程[M].北京:高等教育出版社,2005:206. [2] 蔡果兰,郭继军.二次型与特征函数[J].晋中师专学报,1994(4):19-20. [3] 黄诚,杨春和,童志怡.基于快速Fourier变换的可靠性分析方法[J].固体力学学报,2008(3):319-324. [4] 张弛,吴瑛.利用特征函数识别相位调制信号[J].信息工程大学学报,2008(4):443-446. [5] 陈虹,周常柱.快速查询——特征函数法[J].计算机时代,1997(3):17-20. [6] 周茂袁,王秀丽,李雪艳.特征函数的一种新解释及其应用[J].吉林师范大学学报:自然科学版,2008(2):37-38. (责任编辑:尹晓琦) The Study on the Method for Quantitative Changeof Stochastic Characteristic Function JIANG Tong-bin (School of Mathematics and Physics,Huaiyin Institute of Technology,Huai'an Jiangsu 223003,China) Abstract:The distribution function is uniquely determined by its characteristic function. Prerequisites to judge whether a function is the characteristic function become basic requirements, basic type of a characteristic function and specific determination. The definition of characteristic function, integral transformation and integral methods are used to describe the solution of characteristic functions and their practical application in mathematics, communication, insurance, data inquiry and etc. Key words:characteristic function;distribution function;solution;practical application 中图分类号:O213.2 文献标识码:A 文章编号:1009-7961(2016)01-0081-05 作者简介:蒋同斌(1961-),男,江苏涟水人,副教授,主要从事概概率与统计应用研究。 收稿日期:2015-11-10

