基于多目标优化的冷连轧轧制规程计算方法

金耀辉，刘宝权，宋　君，王奎越，李志锋，吴　萌

（鞍钢集团钢铁研究院，辽宁鞍山114009）



基于多目标优化的冷连轧轧制规程计算方法

金耀辉，刘宝权，宋君，王奎越，李志锋，吴萌

（鞍钢集团钢铁研究院，辽宁鞍山114009）

摘要：以冷连轧现场实际生产情况为出发点，综合考虑板形最优、能耗最小、各种负荷均衡、生产率最高等条件，建立了轧制规程多目标函数模型。在现场设备及工艺条件约束下，结合Nelder-Mead单纯形法对多目标函数进行寻优计算。现场实际应用表明，该轧制规程计算方法计算的轧制规程符合生产要求、速度较快、模型计算结果精度较高，具有广泛的应用前景。

关键词：冷连轧机；轧制规程；目标函数；优化计算；单纯形法

金耀辉，硕士，工程师，2012年毕业于东北大学材料加工工程专业。E-mail：ansteel_jyh@163.com

轧制规程计算(负荷分配及相应的工艺参数计算)是冷连轧机二级过程控制系统的核心内容，也是轧钢生产规范化的首要问题。合理的轧制规程能够提高设备的利用效率，降低生产能耗，保证产品质量精度，稳定生产过程，使轧制过程达到最佳状态，满足轧钢生产中优质、高效、低耗的要求［1-2］。

目前，目标优化法已广泛应用于冷连轧轧制规程的计算，轧制规程优化计算方法是以一个或多个工艺参数，如板形、轧制力、功率、压下率等为优化目标，在满足相应的约束条件下，寻优计算目标函数的最优解的计算方法［3］。其中单目标优化计算方法求解效率高，运行速度快，已广泛应用于实际生产中，但单目标优化方法考虑角度单一，并不能很好地解决轧制规程优化问题。多目标优化计算方法可以兼顾多个性能指标，并得到最优轧制规程计算结果，但目标函数非线性模型具有不连续与不确定性，且求解步骤繁琐，优化程序运行时间较长，不易于在线实现［4］。据此根据某厂轧制生产情况，建立了相应的轧制工艺参数计算模型，构造了基于板形、轧制力、压下率、功率及张力的单目标函数，并在此基础上通过线性加权求和建立多目标函数，采用Nelder-Mead单纯形法对目标函数进行寻优计算，快速、准确的得到目标函数的最优解，在线实现了轧制规程的多目标优化计算。

1　轧制工艺参数计算模型

工艺参数计算模型是冷连轧轧制规程制定的前提，相关工艺参数模型的计算精度直接影响轧制规程的制定效果。本文采用的主要工艺参数计算模型如下：

1.1轧制力模型

轧制力计算模型选用考虑弹性变形区的Bland-Ford-Hill轧制力计算公式为：

(1)塑性区轧制力

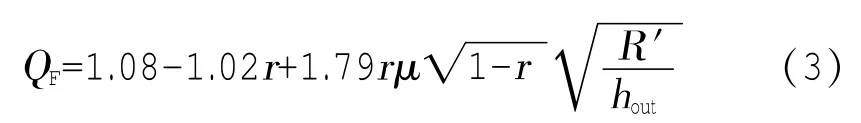
(2)弹性区轧制力

轧辊弹性压扁计算模型采用考虑弹性变形区的Hitchcock公式：

1.2轧制力矩模型

轧制力矩采用Hill轧制力矩公式：

1.3电机功率模型

2　轧制规程多目标函数优化计算方法

2.1目标函数的建立

对轧制规程进行优化前，首先建立目标函数，根据设备和工艺要求确定约束条件，并在此基础上选择优化方法进行计算，从而实现轧制规程的优化计算。

在综合考虑能耗最小、板形最优、各种负荷均衡、生产率最高等因素前提下，建立基于板形良好、轧制力、轧制力均衡、压下量、功率、张力的6个单目标函数。为便于表示目标函数，建立如下中间变量：

(1)基于板形良好的轧制力的目标函数

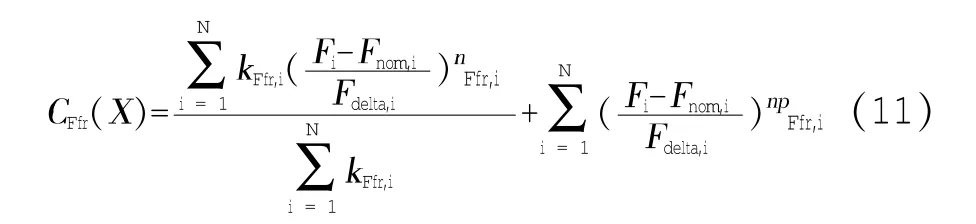
对于末机架为平整模式轧制的情况，末机架中间变量计算方法如下：

(2)基于轧制力的目标函数

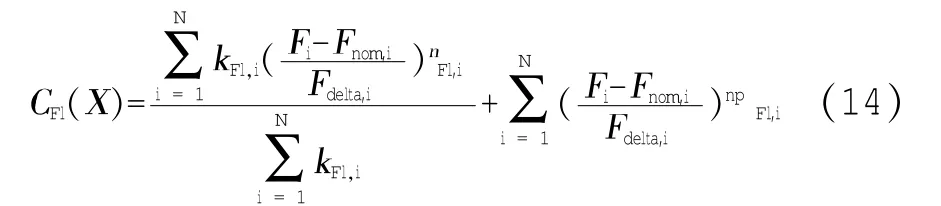
(3)基于轧制力均衡的目标函数

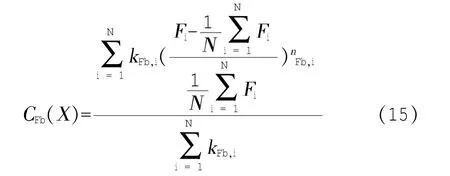
(4)基于压下量的目标函数

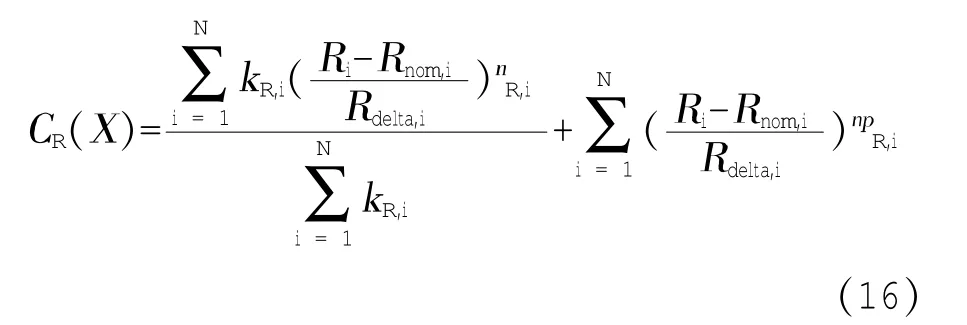
(5)基于功率的目标函数

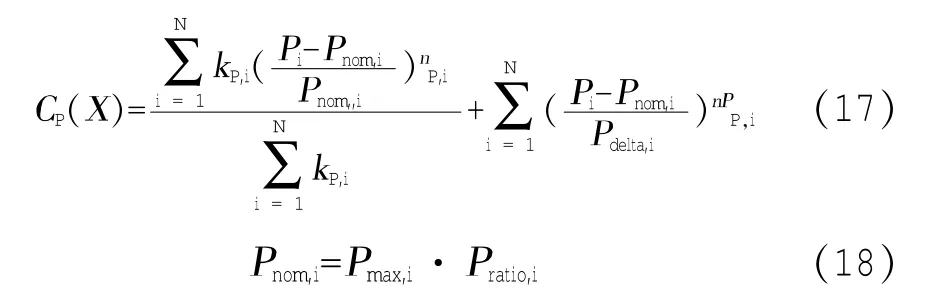
(6)基于张力的目标函数

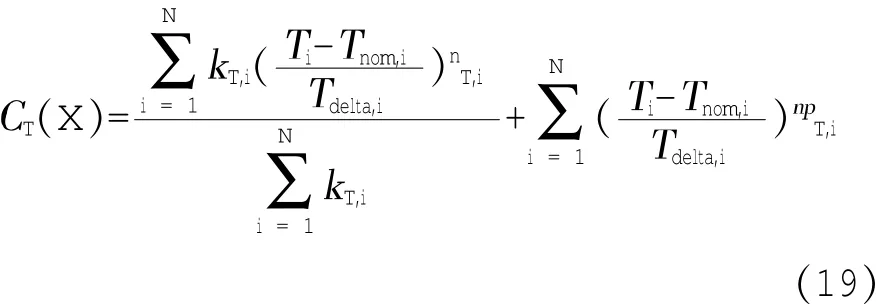
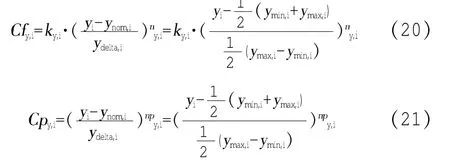
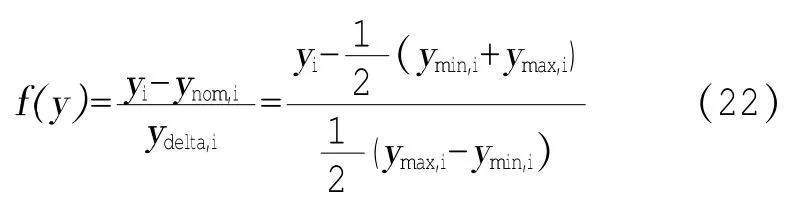
图1为第一机架轧机基于板形良好的轧制力的目标函数值，此时第一机架允许的最大轧制力max=20 000 kN，允许的最小轧制力min=2 000 kN，Ffr=1，Ffr=2，Ffr=40。从图1看出，轧制力超限时，惩罚项的值急剧变化，导致目标函数值呈指数倍增长，此时目标函数值大小主要受惩罚项值的影响；当轧制力在允许范围内时，惩罚项的值很小，此时目标函数值大小主要受目标函数项的值影响。

在如上单目标函数的基础上，建立多目标函数，目标函数结构为：

图1　第一机架轧机基于板形良好的轧制力的目标函数值

在进行轧制规程优化时，需根据实际生产条件对目标函数进行约束［5］，冷连轧生产约束条件主要有设备因素约束和工艺因素约束。

设备因素约束条件有：

工艺因素约束条件有：

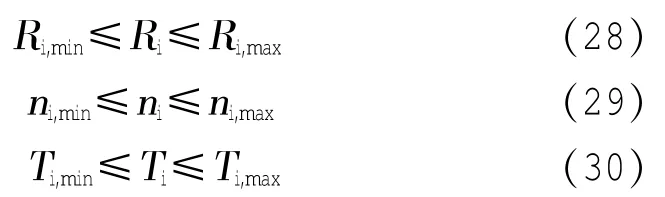
在确定多目标函数及相关约束条件后，本文采用Nelder-Mead单纯形优化计算方法对多目标函数进行优化求解，得到各机架出口带钢厚度及架间张力，进而利用上文提到的轧制工艺参数计算模型，计算出轧制规程相关工艺参数设定值。

2.2优化计算方法

根据冷连轧轧制的特点和目标函数的形式，轧制规程优化算法采用Nelder-Mead单纯形法求解多目标函数的极小值，该算法为直接搜索型非线性优化方法，不必进行微分计算，比较简单，且具有较快的收敛速度［6-7］，适用于现场在线使用。

(2)反射：去除函数最大值对应顶点，得到其余顶点的图形中心点c，W对c进行替换反射，得到：

式中，b为步长系数。令b=1，此时x=xR，计算此时目标函数JR，若JB＜JR＜JN，则点xR替换顶点xW并跳至步骤(5)。

(3)扩展：若JR＜JB＜JN，令b=2，此时x=xE，点xR替换点xE，计算此时目标函数JE，若JE＜JB，则点xE替换顶点xW并跳至步骤(5)。

二维变量Nelder-Mead单纯形法替换计算过程见图2。

图2　二维变量Nelder-Mead单纯形法替换计算过程

3　现场应用

本轧制规程优化计算方法已成功应用于某1450 mm五机架六辊冷连轧生产线，表1为该冷连轧机主要技术参数。

随机选取现场实际生产数据为例，选取钢种CQ，来料厚度2.3 mm，成品厚度0.41 mm，带钢宽度1 060 mm，末机架为平整模式，采用多目标优化计算，其中各目标函数机架加权系数和指数系数见表2。

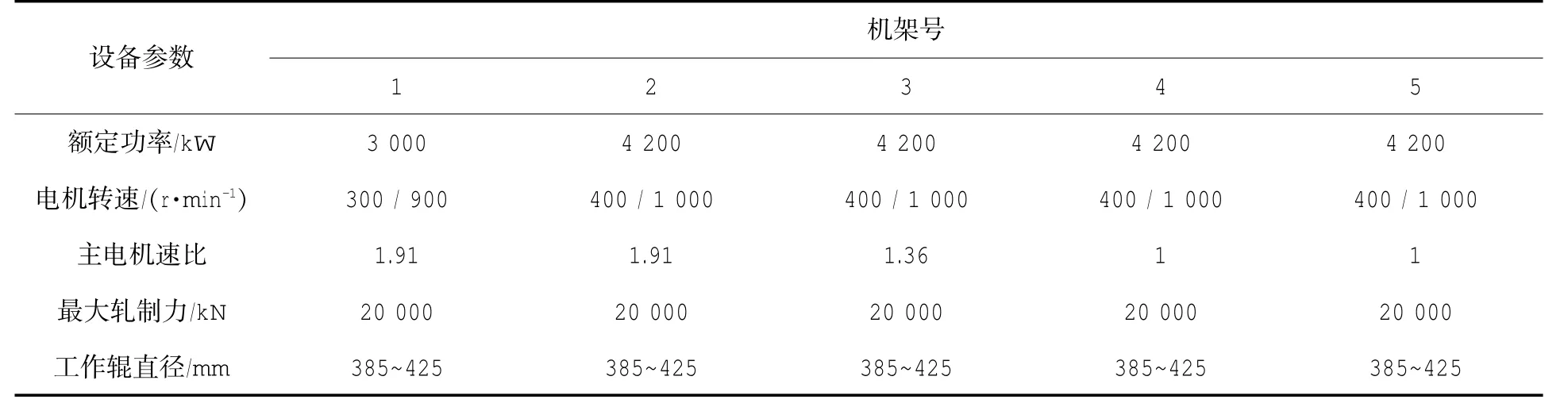
表1　1450 mm冷连轧机主要技术参数

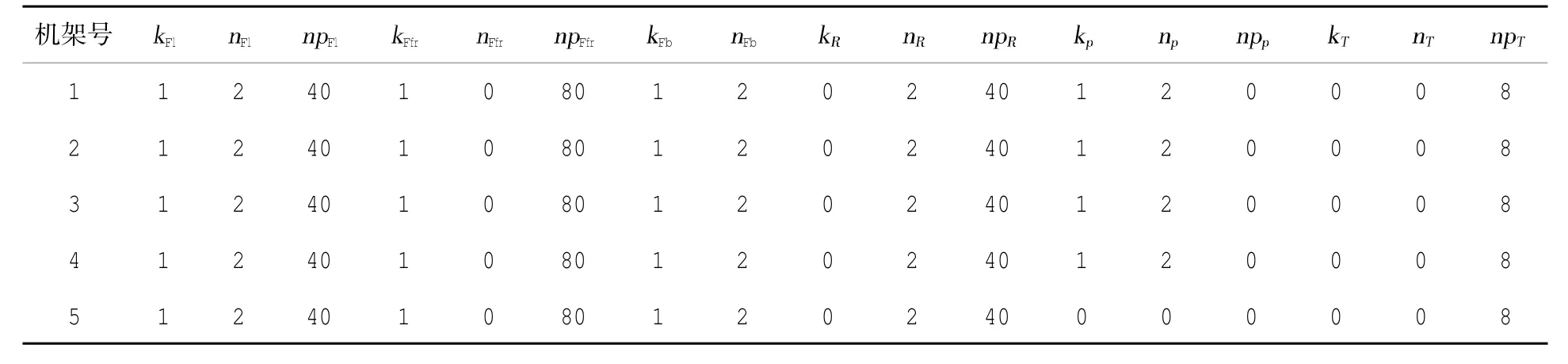
表2　目标函数中的加权系数和指数系数

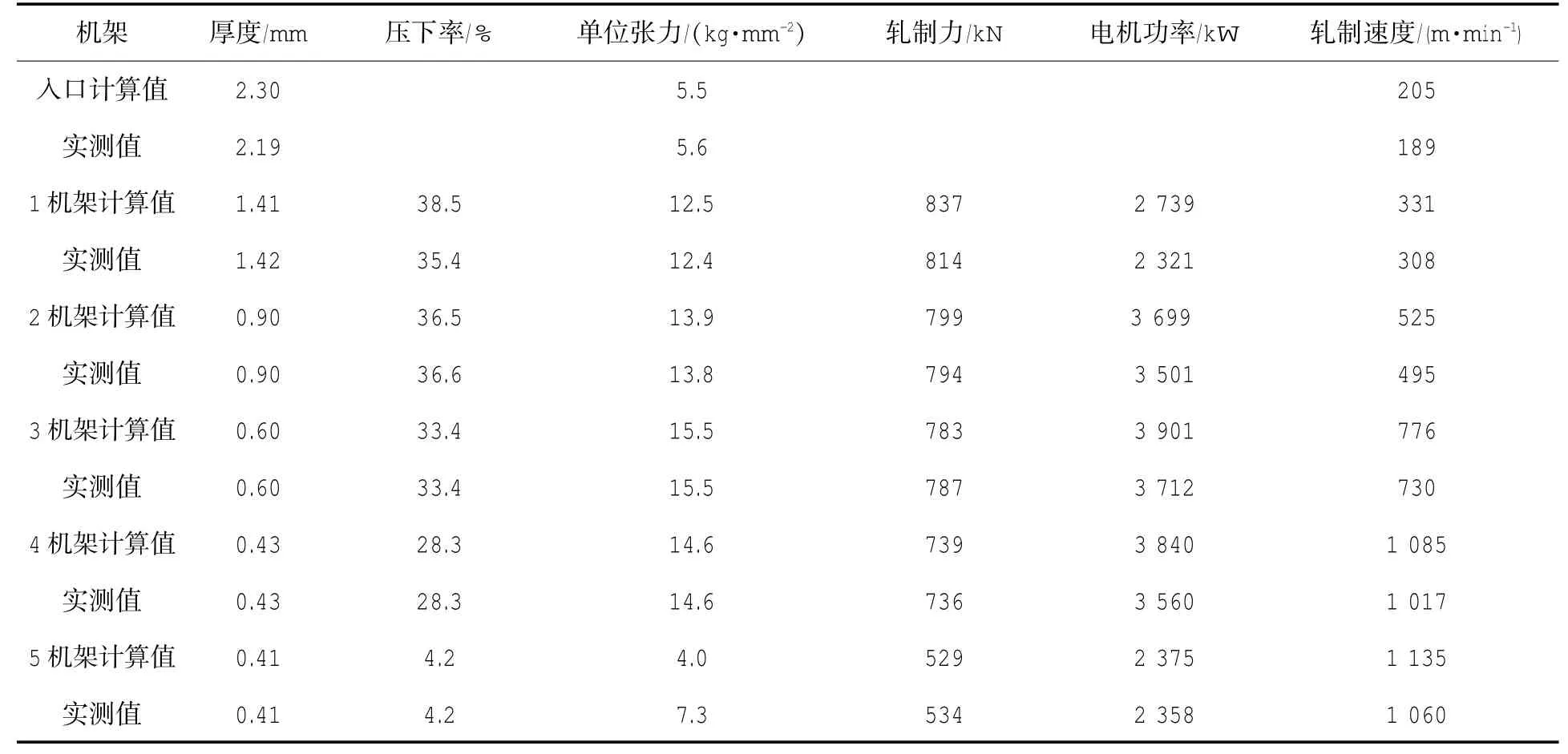
表3　轧制规程计算值与实测值

由表3可以看出，本冷连轧轧制规程优化计算方法，由于使用了符合现场实际的数学模型，因此具有较高精度的优化计算结果。而且，计算的轧制力呈递减规律，符合板形控制理念。平整模式进行轧制时，末机架压下率及轧制力较小，有利于保持良好的板形。合理的利用了各机架电机功率，能够充分发挥各机架电机能力。

4　结论

(1)在建立基于板形良好、轧制力限制、轧制力均衡、压下量、功率、张力6个单目标函数基础上，通过线性加权求和构建了冷连轧轧制规程多目标函数。

(2)通过Nelder-Mead单纯形算法对多目标函数进行寻优计算，得到了满足板形最优、能耗最小、各种负荷均衡、生产率最高等条件的冷连轧轧制规程最优解。

(3)此方法已成功应用于某1450冷连轧生产线，现场实际应用表明，该方法从计算精度、计算时间、求解稳定性等方面均符合在线控制需求，具有广泛的应用前景。

参考文献

［1］王焱,孙一康.基于免疫遗传算法的冷连轧机轧制参数优化方法［J］.信息与控制,2002,32 (2):189-192.

［2］赵新秋,王艳胜,郑剑,等.基于改进混洗蛙跳算法的冷连轧轧制规程优化［J］.钢铁,2012,47(5):49-53.

［3］王军生，白金兰，刘相华.带钢冷连轧原理与过程控制［M］.北京：科学出版社,2009.

［4］李勇，刘建昌，王昱.改进权重自适应GA及冷连轧轧制规程多目标优化［J］.控制理论与应用，2009，26(6)：687-693.

［5］刘晓星.冷连轧机轧制规程的多目标模糊优化设计［J］.钢铁, 2000,35(8):34-36.

［6］Nelde J. A, Mead. R. A simplex method for function minimization［J］.Computer Journal,1965,7(4):308-313.

［7］何坚勇.最优化方法［M］.北京：清华大学出版社,2007.

(编辑袁晓青)

修回日期：2015-05-15

M ethod of Calculation for Rolling Schedule for
Tandem Cold M ill Based on M ulti-objective Optim ization

Jin Yaohui,Liu Baoquan,Song Jun,W ang Kuiyue,Li Zhifeng,W u Meng
(Iron & Steel Research Institutes of Ansteel Group Corporation, Anshan 114009,Liaoning，China)

Abstract:Taking the actual conditions of operations on the site of the tandem cold mill as the first consideration together with comprehensively considering such factors as optimum of strip shape,minimum energy consumption,equilibrium of different loads balance and highest production rate,the multi-objective function model for the rolling schedule was established.Being subject to the equipment on the site and existing technology,the optimizing calculation formultiple objective functions was done by using Nelder-Mead simplex method.According to the actual application of the method of calculation used for the rolling schedule on the site,the rolling schedule calculated by the calculation method above mentioned can meet the requirements required by the production practice,which is characterized by the faster computation speed and higher computational accuracy carried out by the calculation model.So this kind ofmodel has an extensive application prospect.

Key words:tandem cold mill;rolling schedule;objective function;optimization calculation; simplexmethod

中图分类号：TG333

文献标识码：A

文章编号：1006-4613（2016）01-0029-06