基于复形法的结构可靠性指标求解方法

夏雨 龙嘉欣 余颖烨 刘敬敏

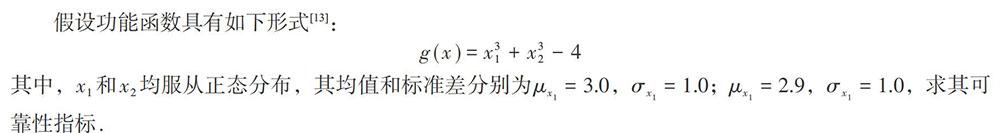
摘要：为了解决在可靠度计算中涉及多维高阶数值计算的极限状态函数的梯度计算，首先使用单纯形法构造初始复形，然后对复形进行寻优迭代计算。通过此方法求解可靠件指标，无需计算极限状态函数的梯度，使计算变得更加简单。通过算例验证了此方法的效率和精度，同时通过工程实例也表明了此方法对实际工程具有一定的适用件。

关键词：复形法;可靠形指标;单纯形法

中图分类号：TU31DOI：10.16375/j.cnkj.cn45-1395/t.2020.01.011

0引言

可靠性指标概念引入用于概率描述可靠度，在研究实际工程应用的计算方法时更加方便。可靠性指标计算方法的提出历经了从简单到复杂或精确的过程，这些方法包含一次二阶矩、二次二阶矩、蒙特卡洛法、遗传算法及其他方法。国内外学者在可靠度的计算上做了一些研究，韦益夫等使用改进移动最小乘二法的响应面来增加样本点的权重并扩大影响域的范围，进而让更多的赋权样本点参与拟合计算，可靠性指标的计算精度更高。罗建斌等将一些结构参数进行优化，得到新的响应面函数，提高計算结果的准确性。许家赫等提出了一种自适应调整权重的PSO算法与fmincon函数的混合算法，优化了模型，一定程度上减少了数值误差。唐承等提出采用序列二次规划方法来提高PSO的局部搜索性能，提高了PSO计算可靠性指标的精度。Keshtegar等提出的基于可靠性方法的MCS和M5Tree改进了用于评估可靠性分析中的性能函数，通过将复杂的隐式问题分解为更小的问题来提供处理复杂隐式问题，提高了可靠性分析的效率。shayanfar等将重要性抽样与定向模拟相结合，围绕设计点的方向进行采样，此混合方法极大地减少调用极限状态函数的次数，与以往的方法相比，更容易得到失效概率。

一次二阶矩方法是目前可靠度分析最常用的方法。但是一次二阶矩方法和二次二阶矩方法都需要计算极限状态函数的一阶偏导数，然而有些极限状态函数难以计算偏导数。可靠性指标的计算中，约束函数往往涉及到高阶多维数值计算过程，约束函数的梯度计算变得困难。所以，通过引入复形法计算可靠性指标，省去了繁琐的梯度计算，在求解可靠性指标上更为简单、方便。

1 复形法的基本原理

可靠性指标的求解属于约束非线性优化问题，本文选择复形法来对其进行计算。此方法打破了以往需要求函数导数的常规，是一种不需要计算目标函数梯度的直接方法，而它的下降方向是通过代入其所有复形的顶点计算目标函数值并进行比较来判断的。

假设n个变量，这些变量将会产生n+1个顶点来构造初始复形。如图1所示，图中为两个变量，那么3个顶点连接起来就构成了一个三角形。将这3个复形的顶点依次代入目标函数中计算，得到目标函数值并比较其大小。由此可以定义最差点X_h为目标函数值最大的点，次差点X_g为目标函数值次大的点，最好点X₁为目标函数值最小的点，并且其变化趋势可以从目标函数值的大小进行大致的判断。若X_c为除最差点X_h以外的每个顶点的形心，那么目标函数值的下降方向通常是由最差点X_h指向形心X的方向。所以在最差点X_h和形心X_c连线的延长线上取一点X_r，并使

X_r=X_c+α（X_c-X_h） （1）

这一个过程称之为反射，在此过程中产生的X_r点称为最差点X_h的反射点。α为反射系数，且一般取α>1.检查反射点X_r是否满足全部约束条件，若反射点X_r满足要求，且

f（X_r）h） （2）则用形心X_c替换最差点X_h，新的复合形组成，完成了一次迭代。如果不等式（2）得不到满足，则应该将反射系数减半。当反射系数减至很小的时候，应再次检查目标函数值是否满足不等式（2），如果目标函数值已满足不等式（2），则新的复合形还是用反射点X_r替换最差点X_h进行构造;如果减到很小的时候（例如当α≤10^-5时），目标函数值仍然达不到式（2）的要求，则新的反射是将次差点X_g代替最差点X_h，通过新的反射，新的迭代过程就组成了。如果反射点X_r不在可行域内，也应该将反射系数α减半。如此反复进行迭代，直至目标函数值达到收敛准则的要求为止。

2改进后的复形法及可靠性指标的计算

在标准正态空间中，坐标原点到极限状态面的最短距离为可靠性指标β的定义。根据此定义，把计算可靠性指标转化为最优数学模型如下：

⑦若单纯形的所有顶点都满足：

g（x）≤0（10）则停止迭代并输出最好点x₁及目标函数值g（x₁），完成初始复形的构造（如图2所示）。

（II）进行复形法的迭代计算

①目标函数为求解可靠性指标β，约束函数则为结构的功能函数g（x），目标函数值是通过复合形各个顶点的代人，从而找出目标函数的最大值β（x_t）及最差点x_t：

β（x_t）=max{β（x_m）（m=1，2，…，n+1）] （11）找出次差点x_b：

β（x_b）=max{β（x_m）（m=1，2，…，n+1;但m≠t）} （12）找出最好点x_w：

β（x_w）=min{β（x_m）（m=1，2，…，n+1）} （13）

②计算除最差点x_t外其他各顶点的形心x_c：把形心x_c代人约束函数g（x）≥0中，检查其可行性。

③如果形心x_c满足约束条件，则沿着（x_c-x_t）方向求得反射点x_r，由式：

x_r=x_c+α（x_c-x_r） （15）式中的反射系数α≥1，可以取α=1.3.如果反射点x_r不满足约束条件，则应将α值减半之后，计算新的反射点x_r，如此反复计算，直到计算所得到的反射点x_r满足所有约束条件为止。如果反射点x_r不满足结构功能函数的所有约束条件，则返回步骤（I）重新构造初始复形。

④把反射点x_r代入目标函数中得到β（x_r），如果

β（x_r）<β（x_t） （16）时，则新的复形是由反射点x_r替换最差点x_h而组成，完成一次迭代后并转入步骤①，否则转入步骤⑤。

⑤如果

β（x_r）>β（x_t） （17）则将α值减半之后，反射点x_r重新计算。这时如果β（x_r）<β（x_t）且反射點x_r满足所有约束条件，则转入步骤④。反射点x_r不满足所有约束条件，则应再将α值减半之后，如此反复计算，得出反射点x_r和目标函数值β（x_r）。如果经过多次减半α值后，并使α值已经缩小到了给定的一个很小的正数ζ（例如ζ=10^-5）以下，仍然得不到满足要求的反射点x_r和目标函数值β（x_r）时，则可将最差点x_t换成次差点x_b并转入步骤②。然后重新进行新的迭代计算，直到得到的反射点x_r和目标函数值β（x_r）满足计算精度为止，如图3所示。即当复合形已经收缩到很小的值时，各顶点的目标函数值均满足

3算例分析

3.1算例1

假设指数型功能函数

g（x）=exp（0.2x+1.4）-x₂其中，变量x₁和x₂均服从标准正态分布，即x_i～N（0，1）（i=1，2），求解可靠性指标。

图4是此算例的迭代过程，采用本文方法无须计算功能函数的梯度，得到了验算点（-1.6798，2.8981），并最终计算得到的可靠性指标为β=3.3497.由表1可以看出，本文方法与其他基本方法计算得到结果是一致的，证明了本文方法的可靠性与实用性。

3.2算例2

似设功能函数具有如下形式：

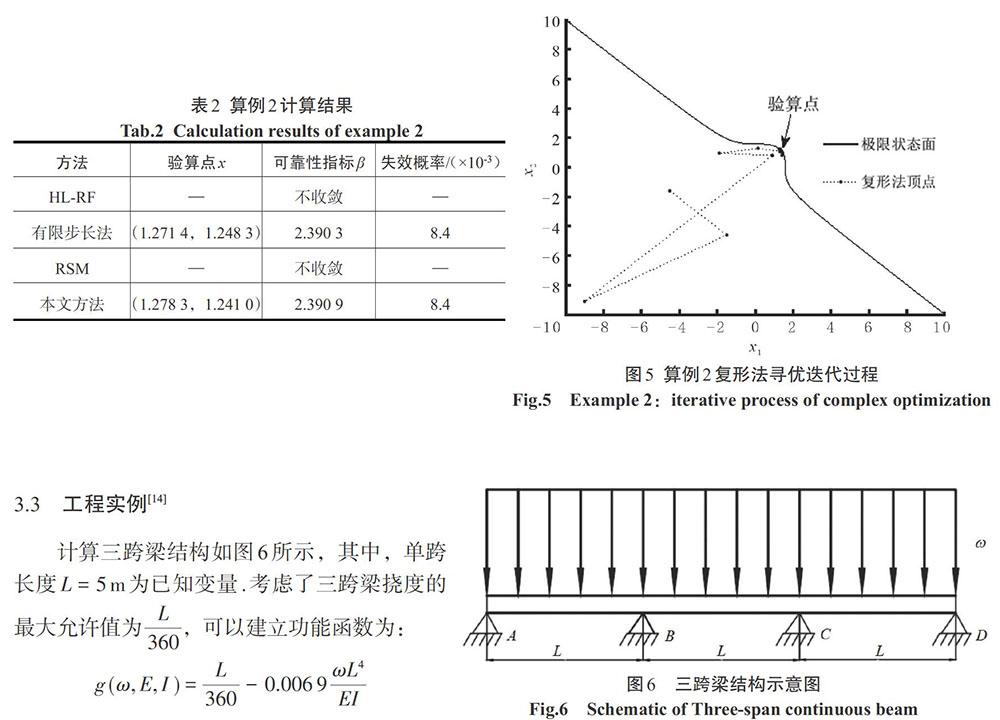
计算结果及复形法寻优迭代过程如表2、图5所示，从表2、图5中可以看出，此二维高阶随机变量问题属于高非线性问题，HL-RF法和经典响应面法因其非线性程度太高而不收敛，但本文方法不仅避开了梯度的计算，而且准确的得到了验算点和可靠性指标。从计算结果表明，本文方法在高非线性功能函数计算得到的精度表现良好且非线性越高表现越好。

3.3工程实例

其中，基本随机变量ω——分布荷载，E——弹性模量，I——惯性矩，均服从正态分布且相互独立，其分布参数如表3所示。

先用单纯形构造初始复形，然后用复合形进行数值迭代计算，得到验算点和可靠性指标。计算结果如表4所示。不难看出，本文方法计算得到的验算点与HL-RF法相差不大，可靠性指标与失效概率与其他方法计算得出的结果一致，而且本文方法无需计算功能函数的梯度。对于多维非线性问题功能函数的可靠性指标求解，本文方法的计算结果精度很高。Monte carlo法的随机性比较大，所以相对于其他方法的精度也会比较低。而本文方法在随机性上做了一定的优化，使得验算点更靠近失效面，并且在实际T程中具有一定的适用性，随着功能函数非线性程度越高，在计算效果方面更显著。

4 结论

一般的结构可靠性指标的求解往往会涉及梯度计算，而本文提出了一种结合复合形建立最优化的数学模型来求解可靠性指标，在此计算过程无需计算任何函数的梯度，使得可靠性指标的求解更加简单、方便。通过几个算例的计算，表明了本文方法在求解多维高非线性问题的可靠性指标时的有效性以及在精度上的优越性，在工程中具有一定的适用性。