Boost变换器的双闭环分数阶PI控制研究

黄钦华 高远 袁海英 文家燕

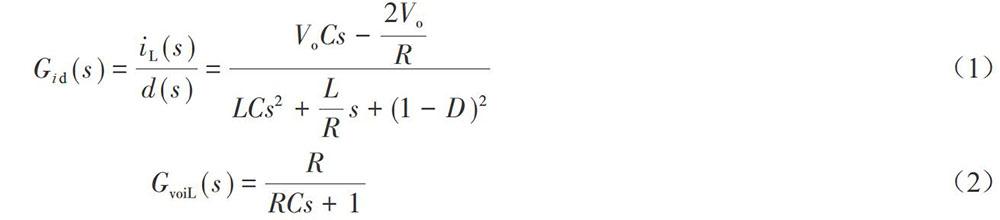
摘要：为提高Boost变换器输出电压的控制性能和抗干扰性，提出一种电压环和电流环均采用分数阶比例积分（PI）控制器的双闭环控制方法。该方法在建立的双闭环分数阶PI控制系统数学模型基础上，结合控制系统频域设计理论设计出电流环、电压环的分数阶PI控制器参数，并利用Bode图分析了被控系统的稳定性和鲁棒性。Boost变换器的双闭环分数阶PI控制仿真结果表明，即使在电源电压、负载，以及期望输出电压的变化条件下，相比双闭环整数阶PI，以及电压环分数阶PI、电流环整数阶PI的两种控制情形，该方法能实现变换器具有更好的输出电压性能和控制鲁棒性。

关键词：Boost变换器;分数阶：双闭环;比例积分控制器：鲁棒性

中图分类号：TM46DOI：10.16375/j.cnki.cn45-1395/t.2020.01.002

0引言

Boost变换器是DC-DC变换器的一种重要类型，通过对其开关器件的通断控制，可实现对直流电源的升压变换输出;在电动汽车、光伏发电系统等领域具有广泛的应用前景Ⅲ。控制策略是实现DC-DC变换器高性能电压输出的重要保证。然而，DC-DC变换器固有的非线性和非最小相位特性，以及系统参数、外部电源和负载的时变性，会使得基于电压单闭环控制的系统电压输出不能有效满足高性能要求的应用工况。近年来，有学者提出了电压和电流反馈的双闭环控制策略，把对变换器电容电压的控制问题转化为对电感电流的控制问题，在一定程度上可降低系统非最小相位特性和时变干扰对控制性能的不良影响。如文献[6]对Boost变换器采用双闭环控制结构，设计一种基于电流模式的非线性控制器，不仅控制输出电压具有良好的动静态性能，而且对电源输入电压的变化也有着较强的输出控制鲁棒性。

目前，DC-DC变换器大都采用整数阶的控制方法。自本世纪以来，人们研究发现分数阶控制相比传统的整数阶控制情形，被控系统具有更好的动态性能和鲁棒性等特点，这极大促进了分数阶理论在电机、飞行器等控制工程领域中的应用。在DC-DC变换器控制领域，基于电压单闭环的分数阶控制已有报道，且可获得相比整数阶控制更好的效果。为克服Boost变换器PI^λD^μ控制器的多控制参数（包含两个分数阶次参数）整定困难，文献[10]通过定义控制性能指标函数，采用粒子群算法进行优化搜索获取控制器参数，研究结果显示PI^λD^μ控制能有效提高变换器的电压输出品质，以及降低系统参数变化对控制的不良影响。文献[11]通过设计外部负载参数的自适应估计律，以及构建分数阶PI滑模函数，推导出Boost变换器的自适应分数阶滑模控制器，可使系统具有良好的电压输出瞬态响应和抗负载变化能力。

为提高Boost变换器的控制性能和鲁棒性，鉴于系统双闭环控制和分数阶控制的优势特点，提出一种电压一电流双闭环分数阶比例积分（PI）控制方法，并根据建立的双闭环分数阶控制系统数学模型，采用频域设计理论，通过分步混合式的设计过程，整定出电流环和电压环的分数阶PI控制器参数。Boost变换器的双闭环分数阶PI控制仿真对比结果验证了所提出方法的有效性。

1Boost变换器双闭环分数阶控制系统的数学建模

图1为包括了Boost变换器的电压、电流双闭环分数阶控制系统原理图。图1中，υ_o和i_L分别为变换器实际的输出电压和电感电流，υ_ref、i_Lref分别表示期望的输出电压和电感电流;电流控制误差e_i（t）=i_Lref-i_L和电压控制误差e_υ（t）=υ_ref-υ_o，分别为电流环控制器和电压环控制器的输入信号，u（t）、i_Lref则分别是电流环控制器和电压环控制器的输出信号;d（t）为u（t）与三角波信号调制作用产生的脉冲宽度调制（PWM）信号，其体现为控制主电路开关器件S通断变化的占空比。假定Boost变换器处电流连续工作模式，利用开关平均建模方法，可获得如下形式的占空比-电流传递函数G_id（s）和电感电流一输出电压传递函数G_voiL（s）。

式中，D、V_o分别为Boost变换器在稳态工作情况下的占空比和输出电压，并有关系V_o=V_in/（1-D）。

图2是Boost变换器双闭环控制系统的数学模型框图。图2中G_c1（s）、G_c2（s）分別表示电流环分数阶控制器和电压环分数阶控制器;G_m（s）=1/V_m是PWM调制器的传递函数，其中载波幅值V_m通常取值为1V。为实现高性能的输出电压控制，电流环和电压环的分数阶控制器设计是技术关键。

1.1双闭环分数阶PI控制器

本文为降低双闭环分数阶控制器的设计复杂性，电流环和电压环均采用分数阶PI控制器，控制器对应的数学表达式分别为

式中，k_p1、k_p2为控制器的比例控制参数，k₁₁、k₁₂为控制器的积分控制参数;λ₁、λ₂∈（0，1）表示分数阶积分的阶次参数。相比整数阶PI控制器，分数阶次参数引入使得控制器具有更好的控制灵活性，特别是当阶次参数为1时，控制器将退变为传统的整数阶PI控制形式。上述的分数阶PI控制器具有的频率特性如下规律：

根据式（5），可进一步求出对应的相频和幅频特性数学表达式：

1.2双闭环分数阶PI控制系统的数学模型

根据图2，结合式（1）、式（3）可求得电流环的闭环传递函数G_iB（s）：

利用式（8）和式（2）可求出电压环被控对象的传递函数数学模型G_v（s）：

G_v（s）=G_iB（s）G_voiL（s）=

进一步可获得G_v（s）的相频特性和幅频特性：

结合上述的系统数学模型，对电压环和电流环的分数阶PI控制器参数进行合理的综合设计是实现变换器获得优良控制性能的重要保证。

2双闭环分数阶PI控制器设计

由控制系统的频域设计理论可知，对于被控系统G（s），当给定期望的截止频率W_c相位裕度ψ_m，根据系统稳定性和鲁棒性的要求，系统开环传递函数、G_o（s）应满足如下的频域设计准则：

1）相位裕度准则

2）鲁棒性准则

3）幅值准则

鉴于双闭环的分数阶PI控制器存在6个待设计参数，若直接从双闭环分数阶控制系统的数学模型出发，利用以上3个频域设计准则，对控制器参数进行严格的解析求解较为困难。因此，为降低控制器参数综合设计的复杂性，同时有别于现有基于智能搜索算法的多参数一步设计方法，本文采取如下具有分步混合特点的设计步骤对双闭环分数阶PI控制器的参数进行设计。

Step 1设计电流环整数阶PI控制器

令式（3）中λ₁=1，取超调量≤5%，阻尼比为0.707的性能要求，结合式（8），采用文献[15]的仿真辅助设计方法，可设计出电流环整数阶PI控制器的k_P1和k_I1参数，即有：

因此，在电流环整数阶PI控制条件下，式（11）可简化为：

进一步可求得G_v（s）的相频特性和幅频特性：

Step 2根据频域设计准则，设计电压环分数阶PI控制器

选取期望的截止频率ω_c和相位裕度ω_m，结合式（18）和式（6），分别根据相位裕度准则式（13）和鲁棒性准则式（14），可求出如下λ_I2与λ₂关系式：

结合式（19）和式（7），根据幅值准则（15）可得到关于K_P2的数学表达式：可首先利用式（20）和式（21）绘制K_I2-λ₂曲线取交点的方法确定k_I2与λ₂，然后再根据式（22）求出k_P2数值。对于λ₂=1的电压环整数阶PI控制情形，可直接通过求解式（20）得到k₁₂。

Step 3选择恰当的分数阶次参数λ₁。，对电流环整数阶PI控制器进行分数阶化

以Step 1所得k_P1和K_I1参数作为电流环分数阶PI控制器的比例和积分控制参数，结合电压环开环传递函数的Bode图，在保持控制稳定性条件下，以增强系统控制鲁棒性为目的，选择恰当的分数阶次参数λ₂，从而实现对电流环整数阶PI控制器的分数阶化。

3设计实例

以系统参数为V_in=60v，，L=2.5mH，C=440uF，R=120Q的Boost变换器为例，并假定变换器处于V₀=120v，D=0.5的稳态工作情况。根据Step 1方法，可设计出电流环整数阶PI控制器表达式：

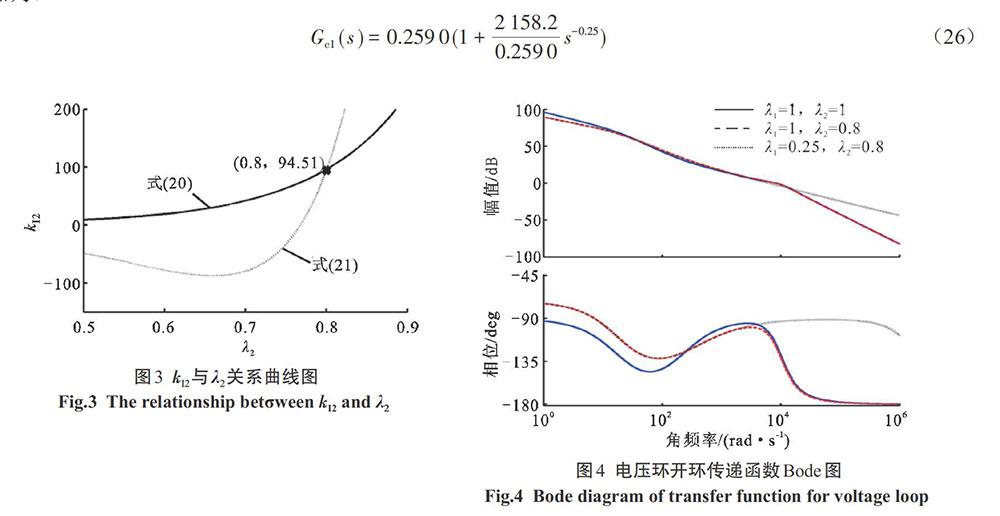
根据Step 2过程，选择ω_c=8300rad/s、ψ_m=π/3，由式（20）和式（21）绘制出如图3所示的K_I2-λ₂的关系曲线图，并由该图交点确定k_I2=94.51、λ₂=0.8后，再根据式（22）可求出k_p2=2.6528.因此，所设计的电压环分数阶PI控制器为：

G_c2（s）=2.6528（1+94.51s^-0.8） （24）

当λ₂=1時，根据式（20）和式（22）可直接设计得到电压环整数阶PI控制器：

G_c2（s）=2.7114（1+543.5226^-1） （25）

依照Step 3的控制器分数阶化方法，选取电流环控制器的分数阶次参数λ₁=0.25，绘制如图4所示的电压环开环传递函数的Bode图。由图4可见，Boost变换器双闭环分数阶PI控制（λ₁=0.25，λ₂=0.8），相比传统的双闭环整数阶PI控制（λ₁=1，λ₂=1），以及电流环整数阶PI、电压环分数阶PI的控制情形（λ₁=1，λ₂=0.8），对应的截止频率ω_c和相位裕度ψ_m均符合设计要求，且相位曲线在截止频率的平坦范围变宽，这表明λ₁=0.25时，可使得双闭环分数阶PI控制系统具有更强的控制鲁棒性。因此，可设计分数阶电流环PI控制器为：

4控制仿真结果及分析

在MATLAB/Simulink环境下，搭建Boost变换器的双闭环分数阶PI控制系统仿真模型，其中分数阶积分数值运算采用Oustaloup滤波算法实现。设置仿真模型的PWM工作频率为40kHz，电源输入电压V_in=60v，负载电阻R=120Ω，期望输出电压V_ref=120v。

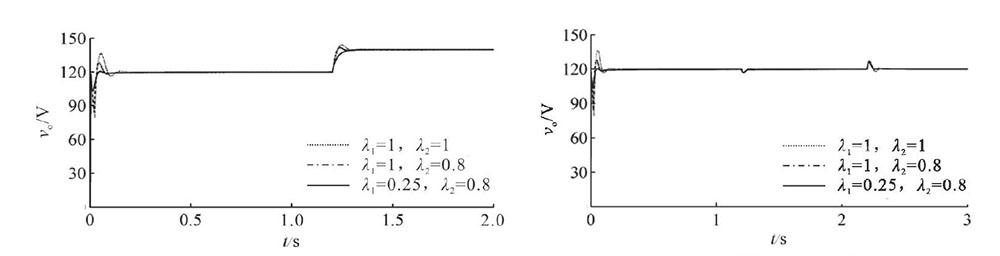
为验证所提控制方法的有效性和先进性，仿真过程中分别考虑了变换器系统期望输出电压、电源电压和负载电阻的变化运行情况，同时还对比系统双闭环整数阶PI，以及电流环整数阶PI、电压环分数阶PI的控制仿真结果。图5示出了调压情况下（V_ref在1.2s时刻由120v跳变至140v）Boost变换器的输出电压响应曲线。图6是负载电阻跳变情况下（R在1.2s时刻由120Ω跳变至100Ω，2.2s时刻再由100Ω跳变至150Ω）的输出电压图。图7给出了电源电压变化时（V_in在1.2s时刻由60v跳变至70v，2.2s时刻再由70v跳变至50v）的输出电压变化情况。

由图5-图7看出，即使在期望输出电压、电源电压和负载电阻的变化情况下，相比双闭环整数阶PI，以及电流环整数阶PI、电压环分数阶PI的控制情形，双闭环分数阶PI控制方法能使得Boost变换器的输出电压具有较快的控制响应速度、更好的对期望输出电压稳定跟踪控制性能，以及抗电源输入电压和外部负载的变化干扰能力。

5结语

针对Boost变换器控制问题，本文提出一种电流环、电压环的双闭环分数阶PI控制方法，并建立Boost变换器双闭环分数阶PI控制系统数学模型。将数学模型与频域设计理论相结合，提出采用一种分步混合式方法设计出电流环和电压环的分数阶PI控制器参数。该参数设计方法有别于现有基于智能优化搜索算法的一步设计‘方法，不需要计算机大量运算;同时可兼顾参数设计的解析性，以及可降低多闭环系统控制参数综合设计过程的复杂性。Boost变换器双闭环分数阶控制系统的控制仿真对比结果表明，本文所提出的双闭环分数阶PI控制方法具有更优的期望输出电压跟踪控制性能和鲁棒性。此外，分数阶PI控制器与整数阶PI控制器的实现结构类似，且分数阶积分环节可采用逼近的数字滤波器技术实现。因此，研究結果为探索DC-DC变换器高性能的控制策略，提供了有用的控制理论方法参考。