基于未知输入观测器的风机变桨系统的鲁棒故障诊断研究

王磊++文传博

摘 要：液压变桨距系统是风力发电机的重要组成部分，对确保风力发电机的高效运行发挥了十分重要的作用。液压变桨距系统是风电机组故障频发的部分，对诊断风机液压变桨系统的故障十分必要。针对建模误差、干扰和噪声等对故障诊断准确性的影响，利用未知输入观测器的方法，将模型不确定性、噪声和未知输入干扰等统一作为系统的未知输入，设计鲁棒残差生成器，使未知输入与液压变桨系统发生的故障相解耦，实现对液压变桨系统的故障诊断，最后通过仿真验证该方法的有效性和优越性。

关键词：液压变桨距系统；故障诊断；未知输入观测器；鲁棒性

中图分类号：TK83 文献标识码：A DOI：10.15913/j.cnki.kjycx.2017.01.028

随着能源危机的加剧，发展低碳和环保的绿色能源迫在眉睫。风力发电具有无污染、可再生等优点，全球都倡导要大力发展风力发电技术，风力发电技术发展的势头迅猛。风电场一般都位于偏远地区，会受到各种恶劣天气的影响。此外，由于不规则变化的风速和风向会对风机产生冲击载荷，所以，风力发电机组故障发生的概率比较高。目前，在风力发电系统中，大型风电机组普遍采用液压变桨距的运行方式。一般情况下，液压变桨系统在风速变化幅度大、频率高的情况下工作，很容易发生故障。风力发电机变桨系统一旦发生故障，其维修将会十分困难，因此，对风力发电机变桨系统进行故障诊断具有十分重要的意义。

目前，基于数据的故障检测方法在变桨距系统中已有许多研究工作，但是，利用基于模型的方法对风力发电机液压变桨系统故障诊断方面的研究却寥寥无几。本文采用未知输入观测器的方法诊断风力发电机液压变桨系统的故障。针对风力发电机液压变桨系统中存在的未知输入干扰、噪声和模型不确定性问题，本文采用未知输入观测器的方法，设计风力发电机液压变桨机构的鲁棒残差生成器，最后通过仿真验证该方法的有效性和优越性。

1 未知输入观测器的基本原理

考虑一般动态系统为：

式（1）中：x（t）为状态向量，x（t）∈Rn；y（t）为输出向量，y（t）∈Rm；u（t）为控制输入向量，u（t）∈RP；d（t）为未知输入向量，d（t）∈Rq；A，B，C，D为分别为相应维度的系数阵；Ed为未知输入矩阵；ξ和η为相互独立的高斯白噪声信号。

全维未知输入观测器的结构如图（1）所示，它的状态空间表达式为：

为了达到未知输入解耦的要求，矩阵H，G，W1，W2和矩阵V必须满足以下4个约束条件：

可检测性，即（C，A）可检测时可以推出（C1，A）可检测，反之亦然。

引理2：假设（C1，A）可检测，其中，A1=A-Ed[（CEd）TCEd]-1（CEd）TCA，并且rank（Ed）=rank（CEd），那么，式（2）所描述的观测器则为系统（1），即式（1）的一个未知输入观测器。

当未知输入到输出的传递函数的极点稳定时，矩阵

列满秩，且特征值均位于S域的左半平面上。

由此不难发现，式（7）等价于矩阵 列满秩，

且特征值均位于S域的左半平面上。

由上述分析过程可知，对矩阵W1的选择并不是唯一，只要在可以保证系统状态矩阵H是稳定的前提下，就可以任意选择W1，然后直接计算出其他矩阵。

2 鲁棒残差生成器的设计

2.1 风机故障模型描述

考虑到故障、干扰、噪声和模型不确定性对故障诊断准确性的影响，针对液压变桨系统故障诊断的风机模型的状态空间方程可描述为：

式（11）中：x=[y1 y2 y3 wr wg θ Tg]T，系统的状态向量分别为3个液压变桨机构的液压缸活塞位移、风轮角速度wr、发电机转动角速度wg、传动系统扭转角θ和发电机的实际扭矩Tg；输出向量y=[y1 y2 y3 xv1 xv2 xv3]T，xv1，xv2，xv3分别是风力发电机3个液压变桨距执行机构的电液比例方向阀阀芯位移；输入向量u=[i Tr Tgr]T；f为故障向量；d为未知输入干扰向量；Ef，Ff为已知故障矩阵；A，B，C，D，Ed为系统的系数矩阵；ξ为过程噪声，η∶N（0，M）；η为测量噪声，η∶N（0，N）；ξ和η为相互独立的高斯白噪声信号。

2.2 鲁棒残差生成器的设计

为了诊断风力发电机液压变桨系统故障，利用未知输入观测器方法设计图2所示的鲁棒残差生成器。

由之前未知输入观测器的介绍可知，选择矩阵W1使得矩阵H具有稳定的特征值对未知观测器设计至关重要。

当（C，A1）不可观测时，可以对系统（C，A1）进行可观性规范分解，进而找到矩阵W1。下面，对（C，A1）进行可观性规范分解，即：

针对风机液压变桨系统故障诊断的未知输入观测器，具体算法步骤是：①计算rank（Ed）和rank（CEd），验证rank（Ed）=rank（CEd）. 当rank（Ed）≠rank（CEd）时，未知输入观测器不存在。②根据式（6），V=Ed[（CEd）TCEd]-1（CEd）T和A1=GA，计算矩阵A1，G和V。③判断系统（C，A）是否可观测，如果（C，A1）可观测，通过极点配置方法计算得到矩阵W1，然后执行步骤⑦；如果（C，A1）不可观测，则执行步骤④。④利用式（12）对（C，A1）进行可观性规范分解。⑤选取n1个期望特征值，对A11- 极点配置，选取相应维度的加

权矩阵Q。⑥根据公式 計算W1. 其中，

为任意（n-n1）×m维矩阵。⑦根据公式H=A-WC和W=W1+HV计算矩阵H和W。

3 阈值设计

在变桨系统的残差评估中，阈值的设定采用RMS值的方法。RMS值的方法是利用一段时间里残差信号的RMS来检测系统的故障，即：

式（16）中：r（t）为应用于液压变桨系统的风机模型与它的故障模型对比产生的残差。

阈值定义为：

当JRMS>Jth，RMS时，系统发生故障，报警；当JRMS≤Jth，RMS时，系统未发生故障，不报警。

4 仿真结果及分析

这里主要是检测风力发电机液压变桨系统的桨距角传感器故障。

仿真中涉及的风力发电机组主要数据为：风力发电机的风轮半径为57.5 m，额定风速为12 m/s，切出风速为25 m/s，额定功率为4.8 MW，额定转速为162 rad/s，空气密度为 1.225 kg/m3，风力机组转动惯量为5.5×107 kg·m2，齿轮比为1∶95，变桨速度为0°/s∶3°/s，桨叶桨距角变化范围为0°∶90°。

高斯白噪声ξ的方差M和高斯白噪声η的方差N的大小设置为：

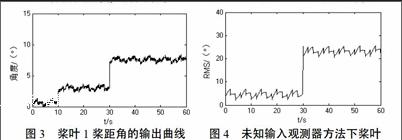
通过改变风机桨叶1的桨距角传感器的反馈系数和滤波时间常数值来模拟风机桨叶1的桨距角传感器故障。在输入信号中加入高斯白噪声，并且当t=15 s时，引入干扰信号；当t=30 s时，对桨叶1的桨距角传感器引入故障，分别对桨叶1桨距角的输出、3个叶片桨距角残差的RMS 、液压缸活塞位移残差的RMS和电液比例方向阀阀芯位移残差的RMS进行仿真分析，仿真结果如图3、图4、图5、图6、图7所示。

由图3可知，当t=15 s时，系统中存在一定幅度的干扰信号，并且系统中的噪声也会对系统输出产生一定的影响。由图4可知，桨叶1的桨距角残差的RMS曲线在t=15 s时无明显变化，并且去除了噪声信号。

对比图3、图4可知，基于未知输入观测器的方法可以诊断桨距角传感器故障，并且使残差信号与噪声、干扰等不确定因素解耦，具有良好的鲁棒性。

由图5、图6、图7可知，当t=30 s时，叶片1的桨距角残差的RMS显著增加，超过阈值，叶片2、叶片3的桨距角残差的RMS、3个桨叶的电液比例方向阀阀芯位移残差的RMS和3个桨叶的液压缸活塞位移残差的RMS均无明显变化，且一直在阈值之下。通过对比、分析图5、图6和图7，可以判断风力发电机液压变桨系统叶片1的桨距角传感器在t=30 s时发生故障。

5 总结

对风机液压变桨系统的故障诊断，不仅要考虑干扰和建模误差，还要考虑噪声等不确定性因素等对故障诊断准确性的影响。针对这个问题，利用未知输入观测器的方法将干扰、噪声和模型的不确定性因素统一视为系统的未知输入，设计鲁棒残差生成器，使未知输入与干扰解耦，通过仿真结果验证了使用该方法进行故障诊断的有效性和优越性。

参考文献

[1]Zhao H，Wu Q，Hu S，et al.Review of energy storage system for wind power integration support.Applied Energy，2015（137）：545-553.

[2]Marques G，Silva F A.Doubly Fed Induction Machine Modeling and Control for Wind Energy Generation [Book News].IEEE Industrial Electronics Magazine，2015，9（3）：54-55.

[3]刘玮.风力发电机组液压变桨距系统的建模以及故障诊断[D].北京：华北电力大学，2009.

[4]李金霞.风力发电机组液压变桨系统的故障诊断方法研究[D].北京：华北电力大学，2013.

[5]Dolz D，Penarrocha I，Sanchis R.Performance Tradeoffs for Networked Jump Observer-Based Fault Diagnosis. IEEE Transactions on Signal Processing，2015，63（10）：2692-2703.

[6]Rahme S，Meskin N.Adaptive sliding mode observer for sensor fault diagnosis of an industrial gas turbine. Control Engineering Practice，2015（38）：57-74.

[7]Willersrud A，Blanke M，Imsland L，et al.Fault diagnosis of downhole drilling incidents using adaptive observers and statistical change detection.Journal of Process Control，2015（30）：90-103.

[8]Liu X，Gao X，Jian H.Robust unknown input observer based fault detection for high-order multi-agent systems with disturbances.Isa Transactions，2016（61）：15-28.

[9]Arrichiello F，Marino A，Pierri F.Observer-Based Decentralized Fault Detection and Isolation Strategy for Networked Multirobot Systems.IEEE Transactions on Control Systems Technology，2015，23（4）：1.

[10]胡志坤，孫岩，姜斌，等.一种基于最优未知输入观测器的故障诊断方法[J].自动化学报，2013（08）：1225-1230.

[11]胡正高，赵国荣，李飞，等.基于自适应未知输入观测器的非线性动态系统故障诊断[J].控制与决策，2016（05）：901-906.

〔编辑：白洁〕