基于稀疏表征的降噪方法及其在振动激励控制中的应用

孟利波，秦毅，合烨，郭磊

(国家山区公路工程技术研究中心，重庆400044)

基于稀疏表征的降噪方法及其在振动激励控制中的应用

孟利波，秦毅，合烨，郭磊

(国家山区公路工程技术研究中心，重庆400044)

针对振动控制中因混有噪声而导致控制精度降低，影响振动控制研究效果的现实问题，提出基于稀疏表征的降噪方法，并通过引入峭度作为测度指标改进基于分离变量的增广拉格朗日收敛算法(SALSA)的基追踪降噪方法。然后，提出获取优化的拉格朗日乘数的方法，从而使得基追踪降噪可以获得更佳的降噪性能。最后将降噪信号反馈给前端控制器，以达到预期的控制目的。通过仿真实例，验证基于SALSA的基追踪降噪方法的有效性。结果表明:将该方法用于水润滑轴承实验的振动控制，能够有效地去除所测力矩信号中不同强度的高斯白噪声，因而可以较好地应用在振动控制中的反馈环节。

稀疏表征;降噪;SALSA算法;峭度;振动控制

0 引言

在研究旋转机械中的轴承、齿轮等零部件的动态特性时，往往需要对该部件进行动态加载。这一过程就是一个振动控制过程。但在振动控制的过程中，扭矩传感器所采集的力信号往往会受到噪声的影响，使得加载力带有随机误差，并最终影响加载精度。因此，必须抑制这些噪声以提高加载器的加载精度。

目前，在振动控制的降噪处理中，广泛是采用小波或小波包进行阈值降噪处理［1－2］。Li和Dang［3］提出改进的小波阈值降噪算法对无线通信信号进行降噪。Xu和Wang［4］将小波阈值和解调技术相结合用于激光信号降噪。Chen等［5］利用斯坦无偏风险估计组提出重叠多小波组阈值降噪方法，并应用于轧机传动系统状态监测。但是以上方法均是采用二进小波变换，这虽然能达到无冗余存贮与重建信号的目的，但随着分解层数的增加，各层、各频段序列的数据点数也减半、采样频率也减半，当数据点数太少时，信号细节会丢失，并且小波分解的结果存在着各频带间能量的交叠问题［6－7］。于是，学者们提出了基于经验模式分解(empirical mode decomposition，EMD)的信号降噪方法。例如，Yang等［8］提出了EMD区间阈值降噪方法;Tian等［9］提出了清晰首区间阈值EMD降噪方法(clear first interval thresholded empirical mode decomposition，EMD－CIIT)。但是EMD存在模态混叠问题，且容易受到强噪声干扰。

自然环境和工程中大部分噪声都是高斯白噪声，目前信号降噪方法也主要针对该类噪声。为了更好地实现自适应信号降噪，本文基于基追踪(BP)问题，采用了一种新的线性凸优化算法——SALSA算法［10－11］，得到了信号的一种稀疏表示，并通过引入谱峭度作为目标函数来改进SALSA算法，从而使改进后的SALSA算法在降噪过程中具备更好的适应性，将其运用在轴承的振动控制中，降噪效果好，计算效率高。

1 稀疏信号

稀疏信号就是指信号可以用少数几个特征向量的线性组合进行表示。信号的稀疏表示，就是找到一种简洁的方式来表示信号，使得绝大部分变换系数的值接近于零或等于零，从而使得到的变换信号是稀疏或者近似稀疏的。

对于某一个信号，均可以用欠定方程表示为

其中，A为M×N矩阵，y为长度为M的向量，x为长度为N的向量，且N＞M。

该系统未知量的个数多于方程的个数，同时矩阵A的宽度大于其长度，当假定AA*可逆时，则方程组有无穷解。

为解决该方程，常用的方法是基于最小二乘的方法。对于本文，为使得信号更加稀疏，采用的是基于基追踪的降噪方法(BPD)。首先需引入范数l1定义为

然后求解式(1)的方法就是使得x的绝对值之和最小，即基追踪(BP)问题，如下式:

当y含有噪声时，这种状况下，需寻求一种近似的目标函数式，该式即为基追踪降噪(BPD)问题:

对于传统的最小二乘法，它是求取平方和的最小值，相比求取绝对值和的最小值，其对信号中的较大值更加敏感，如图1所示。因此，当采用最小二乘法时，为保证平方和最小，需要取得少量的较大值，因为相比于小值，它们的影响更大，因此，最后求取的信号中有更多的小值，也就造成了信号的不稀疏。相反，基于基追踪降噪(BPD)的方法就不会包含很多较小值，从而会获得更加稀疏的信号。针对高斯白噪声信号，本文选用冗余傅里叶变换基进行降噪，该变换基A定义为

式中，0≤m≤M－1和0≤n≤N－1。

图1 和x2函数图像

2 稀疏表征算法——SALSA

由式(4)发现，由于‖x‖1不可微，给计算增加一定难度。并且容易发现，该问题属于凸优化问题，基于这种性质，就有内部局部最小值。此外，对于凸优化问题，目前已有很多算法能够进行求解。例如ISTA［12］和Split Bregman迭代算法［13］，其能够保证在每次迭代后成本函数值的减小，但是这种算法具有收敛慢的缺点。最近兴起的分离变量的增广拉格朗日收敛算法(SALSA)，其与Split Bregman迭代算法均先采用了分离变量，但SALSA的解决方式是基于增广的拉格朗日模型，而该模型是解决优化问题中更基础更标准的工具。在实践的过程中也证明了该算法有很好的收敛性质。

在RN上定义两个凸能量函数f1(x)和f2(x)，其中x为自变量，给出极小化模型:

为分离变量，引入中间变量v，并将v作为函数f2的自变量，这样上式就转化为以下约束问题:

该问题显然等价于问题(6)。欲解决该问题，可以利用增广型拉格朗日模型解决，模型如下:

式中，λ为拉格朗日乘数，μ≥0被称为惩罚参数。

对于该增广型拉格朗日模型，可以引入序列dk，进行迭代，从而达到不断收敛的效果，迭代算法过程如下:

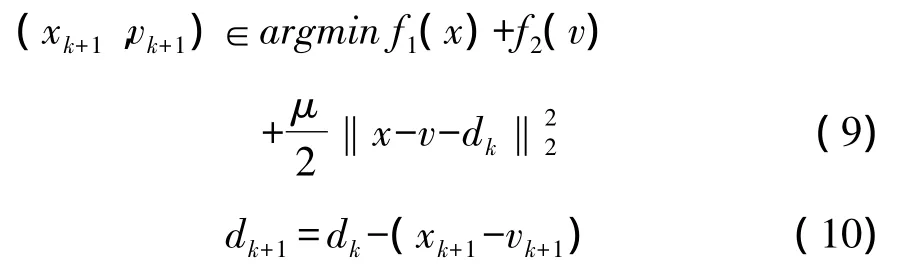
要想很好地利用上述模型，必须能够解决式(9)，可以采用分裂的方法，分别按x和v迭代求极小，从而有效地求得方程的极小值。具体步骤如下:

步骤1:

步骤2:

为了有效解决本文讨论的线性凸优化问题公式(4)，分别令

由此可以建立完整的SALSA迭代计算过程，如图2所示。

相比传统的惩罚函数方法，SALSA迭代算法有很多优点。首先，它基于l1正则项的问题，使得其收敛速度很快。当其收敛很快时，就可以直接利用无约束问题。其次，λ是一个固定常数，只需选择一个合适的值使得条件数达到最少，从而使迭代优化算法快速收敛。通过计算出的x就可以估算出原始信号^y=Ax。

图2 SALSA算法流程图

3 利用SALSA算法进行去噪仿真

现有一组含有500个采样点的音频信号，其采样率为16 000，持续时间约为31 ms，用s(m)表示，图形如图3(a)所示，可以看出该音频信号主要集中在低频部分，但高频部分仍有部分微弱的信号。用w(m)表示采样点数为500的高斯噪声信号，由于其具有随机性，因此会造成信号的不稀疏。可用y(m)表示含有噪声的信号如式(12)，其图形如图3(d)所示，频域图涵盖整个范围，造成信号的不稀疏。

图3 原始信号、加噪信号、降噪信号的时域波形以及对应的频域图

然后利用SALSA算法对其进行稀疏表征。采用50次迭代，得到降噪信号，如图3(e)所示。可以看出，噪声信号大大削减，而波形的基本形状几乎没发生变化，并且与低通滤波不同，高频部分并没有完全衰减，仍然保留了原始信号中的部分高频成分。

4 基于谱峭度的算法优化

前面已经讨论过，在使用SALSA算法时，需选取合适的λ。经过多次试验发现:若选择较大的λ，则降噪后的信号，不仅噪声大大衰减;有用信号也大大衰减;反之，若选择较小的λ，将不能完全把噪声滤除。

峭度(kur)表示故障形成的大幅值脉冲出现的概率，按下式定义为

式中，Xi为原信号，为信号均值。为了将脉冲响应与背景噪声的差距拉大以提高信噪比，峭度系数取脉冲响应幅值的4次方为判断依据，准确度大大提高。于是在寻求算法优化阶段同时引入了信噪比和峭度来寻找最佳λ。

在仿真实验中引入余弦信号作为模拟仿真信号，将其与随机信号进行叠加得到一个模拟试验中的信号。在仿真实验中引入一个比例参数rate:

从图中可见，结论1)是成立的。在同样的噪声和λ取值范围下，令余弦信号幅值取值范围为(1.0，0.9，…，0.1)，此时所得近似最佳λ(1 030)，如表1所示。从表中可知，在随机信号一定时，rate值不会发生很大的变化，由rate值求出的近似最佳λ也是非常接近在信噪比与λ关系图上得出的最佳λ(1 030)，于是，在真实信号未知的情况下可以参考模拟仿真信号下得到的rate值反求出一个十分接近最佳真实值的λ，从而获得优化的降噪结果。

图4 余弦信号取不同幅值时降噪结果信噪比随λ变化的示意图

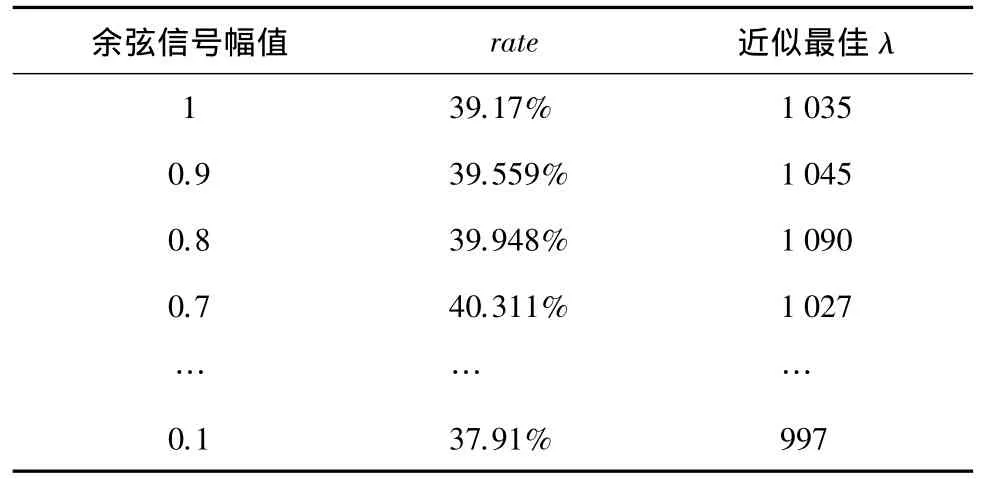
表1 不同余弦信号幅值对应的近似最佳λ

5 实验验证

将上述降噪方法运用在水润滑轴承激励控制中，实验平台如图5所示。该实验台能够通过二通道电液伺服协调加载系统对实验轴进行静态加载和动态激励。在进行动态激励时，可根据需要，选择相应的波形，如正弦波、三角波、方波等进行激励。

图5 轴承加载实验台

对于本实验，可采用15 Hz的正弦波进行激励。通过扭矩传感器采集到的力矩信号如图6(a)所示，通过选定一系列的λ值进行降噪，预估噪声强度为0.7。根据前述方法求得真实信号近似最佳λ值为110。通过扭矩传感器采集到的力矩信号和采用本文方法获得的降噪信号如图6(b)所示。可以看出，所加载的力矩由于受到噪声污染，含有许多毛刺，但经过本文的方法处理后，具有明显的降噪效果。将降噪后的信号反馈给前端控制器，用来不断修正被控量与输入量之间的偏差，从而能够达到更准确的控制效果。

图6 低噪声时实测信号与降噪信号

为了进一步验证本文所提方法的有效性，通过调整信号调理装置，增加噪声强度，所测得信号如图7(a)所示。采用本文方法所得降噪结果如图7(b)所示。同样地，可以将降噪后的信号反馈给前端控制器，以提高控制精度。

图7 高噪声时实测信号与降噪信号

6 结束语

对于混有噪声的振动控制信号，利用本文叙述的方法可以达到良好的降噪效果，可见引入峭度和反求最佳λ值的方法，使得降噪效果更加明显，更加具有适应性，最后将降噪信号反馈给前端控制器，用来不断修正被控量与输入量之间的偏差，从而能够提高控制精度。该方法的不足之处在于，为了获取最佳λ，通常要使λ取值范围较大，这就会显著地增加计算量。但是就目前计算机性能而言，该方法仍然具有很快的计算速度。

［1］刘爱平，邹立华，戴素亮，等.振动控制研究中的小波包降噪处理［J］.振动与冲击，2008，27(2):95－97.

［2］冯永胜，董云峰.小波降噪在雷达制导空空导弹导引头上的应用［J］.战术与导弹技术，2007(6):76－80.

［3］LI R J，DANG A H.A blind detection scheme based on modified wavelet denoising algorithm for wireless optical communications［J］.Optics Communications，2015，353 (15):165－170.

［4］XU F，WANG Y Q.Signal enhancement of a novel multiaddress codinglidar backscatters based on a combined technique of demodulation and wavelet de－noising［J］.Optics and Lasers in Engineering，2015(74):122－129.

［5］CHEN J L，WAN Z G，PAN J，et al.Customized maximaloverlapmultiwavelet denoising with data－driven group threshold for condition monitoring of rolling mill drivetrain［J］.Mechanical Systems and Signal Processing，2016，(68－69):44－67.

［6］INOUE T，SUEOKA A，KANEMOTO H，et al.Detection of minute signs of a small fault in a periodic or aquasiperiodic signal by the harmonic wavelet transform［J］.Mechanical System and Signal Processing，2007，21(5): 2041－2055.

［7］张文斌，周晓军，杨先勇，等.基于谐波窗方法的转子轴心轨迹提纯［J］.振动与冲击，2009，28(8):74－77.

［8］YANG G L，LIU Y Y，WANG Y Y，et al.EMD interval thresholding denoising based on similarity measure to select relevant modes［J］.Signal Processing，2015(109):95－109

［9］TIAN P F，ZHANG L，CAO X J，et al.The Application of EMD－CIIT Lidar Signal Denoising Method in Aerosol Detection［J］.Procedia Engineering，2015(102):1233－1237.

［10］AFONSO M V，BIOUCAS D J M，FIGUEIREDO M A T.Fast image recovery using variable splitting and constrained optimization［J］.IEEE TransImage Process，2010，19(9): 2345－2356.

［11］AFONSO M V，BIOUCAS－D J M，FIGUEIREDO M A T.An augmented Lagrangian approach to the constrained optimization formulation of imaging inverse problems［J］.IEEE Trans Image Process，2011，20(3):681－695.

［12］BECKA，TEBOULLE M.A fast iterative shrinkage thresholding algorithm for linear inverse problems［J］.SIAM Journal on Imaging Science，2009，2(1):183–202.

［13］GOLDSTEIN T，OSHER S.The split Bregman algorithm method for L1 regularized problems［J］.SIAM Journal on Imaging Sciences，2009，2(2):323－343.

(编辑:李妮)

De－noising method based on sparse representation and its application invibration control

MENG Libo，QIN Yi，HE Ye，GUO Lei
(National Engineering and Research Center for Mountainous Highways，Chongqing 400044，China)

Aimed at the fact that the control accuracy declines due to the noise effect on the vibration control，a de－noising method based on sparse representation is put forward to improve the control signal.To obtain a better noise－reduction result，the basis pursuit denoising method based on split variable augmented Lagrangian shrinkage algorithm(SALSA)is improved by using kurtosis as measurement index.Then，a method for obtaining the optimized Lagrange multiplier parameter is proposed，which can improve the denoising performance of basis pursuit denoising.Finally the de－noising signal is fed back into the front controller in order to obtain the expected control effect.The simulation result validates the effectiveness of basis pursuit denoising based on SALSA.Finally，the proposed method is applied to the vibration control of a water water－lubricated bearing test，and the results show that this method can effectively remove the noises with different intensity from the sampled torque signals，thus it can be well used in the feedback element of the vibration control.

sparse representation;de－noising;SALSA algorithm;kurtosis;vibration control

A

1674－5124(2016)11－0094－06

10.11857/j.issn.1674－5124.2016.11.020

2016－01－07;

2016－03－04

国家山区公路工程技术研究中心(GSGZJ－2014－04)

孟利波(1977－)，男，重庆市人，研究员，博士，研究方向为结构监测与控制。