基于IPSO－SVR的水泥窑尾分解率软测量研究

金星，徐婷，王盛慧，李冰岩，秦石凌，张永恒

(长春工业大学电气与电子工程学院，吉林长春130012)

基于IPSO－SVR的水泥窑尾分解率软测量研究

金星，徐婷，王盛慧，李冰岩，秦石凌，张永恒

(长春工业大学电气与电子工程学院，吉林长春130012)

为实现水泥窑尾分解率的实时在线检测，利用软测量技术在解决工业在线测量问题中的优势，提出一种改进的粒子群参数优化的支持向量回归机算法(IPSO－SVR)，即通过粒子群算法对支持向量机模型核心参数进行优化选择，并在粒子群算法中引入自适应惯性权重的思想，克服粒子群算法容易出现早熟收敛、陷入局部极值的缺点，最终建立起基于IPSO－SVR的窑尾分解率软测量模型。将其与基于交叉验证法(CV)和未改进粒子群算法优化SVR参数的软测量模型进行仿真对比实验，实验表明:该IPSO－SVR模型具有更佳的预测能力，窑尾分解率预测相关系数达0.857 5，预测最大相对误差不超过1.14%，平均相对误差为0.75%，可进一步运用到诸如水泥生产等大型工业的产品分解率预测中。

在线检测;窑尾分解率;软测量;粒子群算法;支持向量回归机

0 引言

预分解技术作为新型干法水泥生产工艺的核心技术，是在悬浮预热器和回转窑之间增加了新热源——分解炉，旨在提高窑尾分解率。增加分解炉设备，减轻了窑内烧成带的热负荷，大幅度提高了窑系统的生产效率，所以窑尾分解率的高低及其稳定情况成为控制分解炉及回转窑的重要参考量［1］。

窑尾分解率作为与系统稳定及产品质量密切相关的重要过程变量，需对其进行实时准确的检测。而目前对窑尾分解率的检测方法主要集中在烧矢量法、CO2增量法以及CO2气体吸收法等传统的方法，尚无统一的国家标准。此外，文献［2－3］中分别提出了采用BS－I型测碳仪和钙铁分析仪测定分解率，不但测定速度快而且简单。然而，以上方法均属于离线检测方法，既耗费资源，测量结果又存在一定的滞后性，并不能很好地满足工业过程实时控制的需求。

软测量技术的发展为窑尾分解率实时在线检测提供了新的思路［4］。所谓软测量技术就是通过工业生产中的可控变量及可测变量，使用机理建模、数理统计建模、神经网络建模等方法计算或估计无法在现阶段实时检测的待测变量。文献［5］基于软测量技术，提出了钢水温度的软测量方法;文献［6］介绍了软测量技术在聚酯工业过程中的应用。

结合窑尾分解率检测方法的研究现状和与窑尾分解率密切相关的几个主要运行参数，参考已有研究，本文提出一种改进的粒子群参数优化的支持向量回归机算法(IPSO－SVR)，在引入自适应权重思想克服粒子群算法容易出现早熟收敛、陷入局部极值的缺点［7］，提高其全局搜索能力和局部改良能力的基础上，对支持向量回归机进行参数优化，进而建立窑尾分解率软测量模型。

1 IPSO－SVR算法

1.1 支持向量回归机

当支持向量机(SVM)通过引入一个额外的损失函数以应用到回归运算中时，称为支持向量回归机(SVR)。ε－SVR是应用最普遍的SVR模型之一，当数据集{xj，yj}呈线性关系时，回归方程［8］可描述为

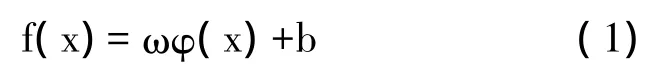
式中:ω——向量回归系数:

b——偏差。

优化对象可以表示为

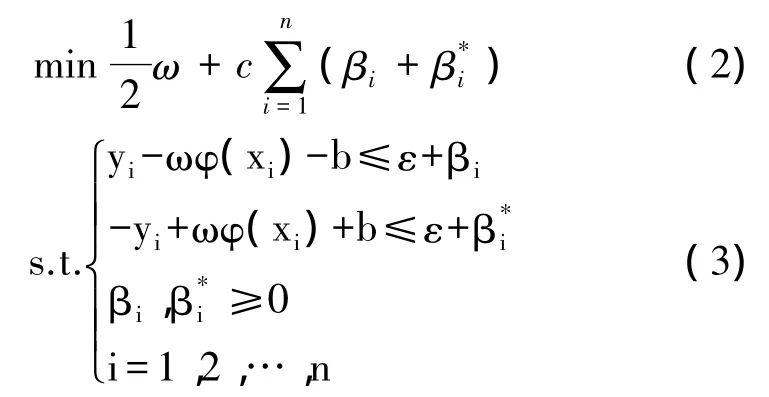
式中:ε——不敏感损失系数;

c——对误差大于ε的样本的惩罚程度，常数，

正值;

对于非线性情况，可以通过核函数转换成线性。鉴于径向基核函数较其他核函数更好的性能表现，本文选取径向基核函数作为SVR的核函数:

1.2 改进粒子群算法(IPSO)

1995年Kennedy和Eberhart提出粒子群算法(PSO)。粒子群算法的中心思想是通过最小的适应度函数获取最优解(粒子)［9］。每个粒子的速度和位置通过以下公式进行更新:

式中:c1、c2——学习因子;

r1、r2——0和1之间的随机数;

ω——惯性权重系数;

gbestk——直到所有粒子第k次迭代后的全局最优解。

为了平衡粒子群算法的全局搜索能力和局部改良能力，引入非线性动态惯性权重系数公式(7)对ω进行更新，因ω随粒子的适应度函数值自动变化，故又称之为自适应惯性权重。

式中:ωmin=0.4，ωmax=0.9;

f——粒子当前的适应度函数值;

favg、fmin——当前所有粒子的平均适应度函数值和最小适应度函数值。

当各粒子的适应度函数值比较分散时，ω减小;当各粒子的适应度函数值趋于一致或局部最优时，ω增大。同时对于适应度函数值优于平均适应度函数值的粒子，其对应的ω较小，从而保留该粒子。反之，对于适应度函数值差于平均目标值的粒子，其对应的ω较大，使该粒子向较好的搜索区域靠拢。

1.3 IPSO优化SVR模型

SVR的泛化能力完全依赖于不敏感损失系数ε、惩罚系数c和RBF核宽度系数σ3个参数，因此，寻求最优化的参数对(ε，c，σ)是实现支持向量回归机的关键。本文中，采用IPSO对该参数对(ε，c，σ)同时寻优，选取能够直接反应SVR回归性能的均方差(MSE)作为适应度函数:

式中:n——样本的数量;

yi——第i个样本实际测量值;

^y——第i个样本的预测值。

基于IPSO的ε－SVR参数对(ε，c，σ)迭代优化选取步骤可总结如下:

1)初始化粒子群(ε，c，σ)，确定最大迭代次数tmax和种群规模m等算法相关参数值;

2)将每个粒子的个体极值pibest设置为其当前值，按式(8)计算各粒子的适应值，将全局极值gbest设置为适应度最好的粒子的个体极值;

3)按照式(5)～式(7)对粒子的速度和位置以及惯性权重ω进行更新;

4)依据适应度函数(MSE)评价更新粒子的适应值;

5)将更新后粒子的适应值与其极值pibest对比，择优作为新的个体极值;

6)将新的个体极值pibest与当前全局极值gbest对比，择优作为新的全局极值;

7)判断是否达到最大迭代次数或适应值不再变化，达到则终止，否则返回3)。

2 分解率预测仿真实验及结果分析

2.1 变量选取

分解炉作为预分解系统的核心部分，主要承担煤粉燃烧、气固换热和生料分解任务。水泥生料分解过程中主要的化学反应为碳酸钙的分解反应，其分解过程为可逆反应，并且分解反应为强吸热过程，只有保持适当高的温度和周围介质中合适的CO2分压才利于反应的正向进行。随着温度的升高，碳酸钙开始分解，通常情况下，温度控制在850～900℃时，最利于分解反应的快速稳定进行［10］。因此，本文选取温度和压力作为影响水泥窑尾分解率的主要参考变量。

同时，生料进料量也是影响生料分解率的重要参量，加大进料量，若炉内反应物不能充分反应则使分解率降低，反之，分解率升高。由于生料进料量与提升机电流的正比关系，选取易于测量的提升机电流作为辅助变量之一［11］。

2.2 数据采集

本文以吉林省亚泰水泥有限公司双阳建材公司2000 t/d新型干法水泥生产线为研究对象，实验所用的分解率化验室离线采样分析值和相应时刻的DCS历史数据均来自该生产线，由于分解率所需的化验室分析时间较长而DCS系统数据采样周期较短，故取分解率采样时刻前后20 min的数据平均值作为辅助变量，选取对应该采样时刻窑尾分解率化验值作为主导变量，选取有代表性的230×7组数据用作仿真实验，实验数据如图1所示。

图1 窑尾分解率软测量输入输出数据

2.3 数据预处理

鉴于数据样本量纲和单位不统一问题，对样本数据进行归一化，归一化处理后，所有样本数据被转换为(0，1)之间的小数，考虑到预测集归一化处理后对应的数据最值存在超出训练集归一化处理后的数据范围的情况，即最终训练出的SVR模型不足以满足预测集的要求，本文将训练集和预测集统一按维度进行归一化，归一化公式为

式中:xi、——数据样本归一化前后的值;

xmin、xmax——数据样本中的最小值和最大值。

2.4 预测结果及分析

为避免初始化粒子群盲目性，选择文献［12］中提供的参数大致范围ε=［0，0.2］，c=［1，108］，σ=［0.01，2.0］。实验选取种群数量为20，终止迭代次数为100。经粒子群算法优化选择后寻得最优参数值为ε=0.148 22，c=67.830 1，σ=23.508 9。将寻得的最优值分别赋给SVR模型的3个参数，并从这230组实验数据中随机选取150组数据构成训练集，另80组数据构成预测集分别进行训练和预测仿真实验，实验效果如图2所示。

图2 基于IPSO－SVR模型训练与预测效果图

2.5 对比试验分析

由2.4的实验结果可以看出，利用改进的粒子群算法对SVR参数寻优建立的窑尾分解率软测量模型具有很好的回归和预测效果。为了进一步验证该改进方法的优势，将其与基于CV－SVR和未改进的PSO－SVR软测量模型的预测效果进行对比试验，预测效果对比与误差分析如图3～图5所示。

从图3和图4中不难看出，基于IPSO－SVR的窑尾分解率软测量模型表现出更好的预测效果，对水泥窑尾分解率的预测值更接近实际分解率化验值。图5中通过分解率预测误差的对比图更明显地体现出改进模型的优势，实验性能评价参数对比总结见表1。

图3 基于IPSO－SVR与基于CV－SVR软测量模型预测效果对比图

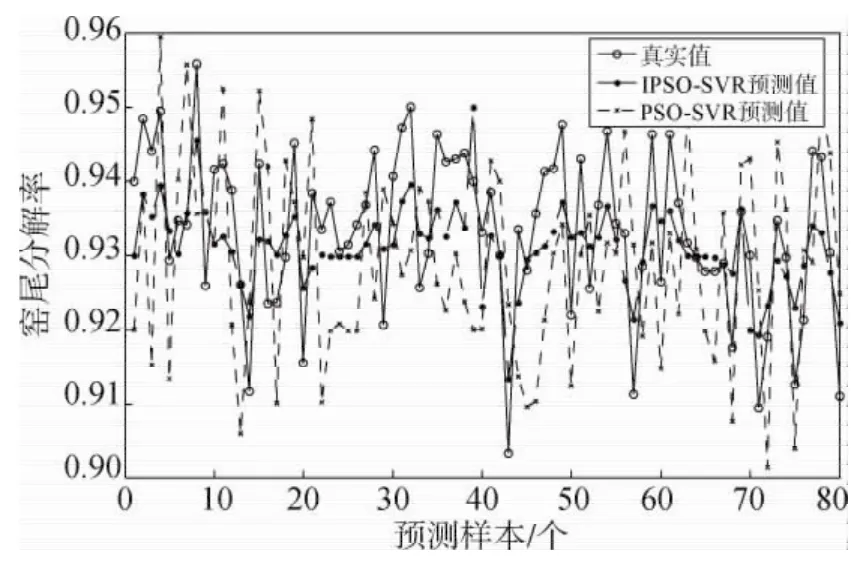
图4 基于IPSO－SVR与基于PSO－SVR软测量模型预测效果对比图

图5 窑尾分解率预测误差对比图

表1 模型预测性能对比

如表所示，在对水泥窑尾分解率进行预测时，3种软测量模型都达到了一定的预测效果，同时，基于IPSO－SVR的软测量模型的各项性能评价指标都明显高于其他两种软测量模型，与实际化验分解率曲线相关系数达0.8575，分解率预测相对误差保持在1.14%以内，平均相对误差0.75%，获得了很好的预测精度。

3 结束语

本文依据与窑尾分解率密切相关的主要运行参数，提出了一种IPSO－SVR算法做窑尾分解率软测量回归模型和预测。通过实验和在相同预测集情况下，与另外两种窑尾分解率软测量预测模型进行对照实验分析，该IPSO－SVR算法表现出了更佳的建模、预测与泛化能力，分解率预测平均相对误差0.75%。所提出的方法适用于水泥窑尾分解率软测量预测模型的建立，并可进一步运用到诸如水泥生产等大型工业的产品分解率实时在线检测中。

［1］李斌怀，郭俊才.预分解窑水泥生产综合技术及操作实例［M］.武汉:武汉理工大学出版社，2006:132－141.

［2］刘文长，张亚珍，游良俭.用BS－I型测碳仪测定入窑生料分解率［J］.水泥，2003(5):39－40.

［3］刘洪林，于加滨.氧化钙法快速测定入窑生料分解率［J］.四川水泥，2004(2):53.

［4］曹宏芳，付忠广，齐敏芳.PSO－SVM软测量方法在火电厂煤质发热量测量中的应用［J］.热能动力工程，2014，6(29):731－735.

［5］孙彦广，高克伟，陶百生.基于智能技术的刚水温度软测量［J］.仪器仪表学报，2002(S2):753－755.

［6］周志成.基于支持向量机的软测量建模［J］.自动化技术与应用，2005，24(8):8－10.

［7］孟倩，马小平，周延.改进的粒子群支持向量机预测瓦斯涌出量［J］.矿业安全与环保，2015，42(2):2－4.

［8］PEI J F，ZHU Y M.Modeling and prediction the glass transition temperature of vinyl polymers by using hybrid PSO－SVR method［J］.Journal of Theoretical and Computational Chemistry，2013，12(3):5－13.

［9］QIN T C，ZENG S K.Robust prognostics for state of health estimation of lithium－ion batteries based on an improved PSO－SVR model［J］.Microelectronics Reliability，2015，55 (3):1280－1284.

［10］段鹏君.水泥生料分解率温度过程建模方法研究［D］.沈阳:东北大学，2012.

［11］刘慧.新型干法水泥生产窑尾分解率软测量研究［D］.济南:济南大学，2010.

［12］熊伟丽，徐保国.基于PSO的SVR参数优化选择方法研究［J］.系统仿真学报，2006，18(9):2442－2445.

(编辑:莫婕)

Soft sensor measurement research on resolution ratio of cement kiln tail based on IPSO－SVR

JIN Xing，XU Ting，WANG Shenghui，LI Bingyan，QIN Shiling，ZHANG Yongheng
(College of Electrical and Electronic Engineering，Changchun University of Technology，Changchun 130012，China)

A support vector regression(SVR)algorithm optimized by improved particle swarm optimization(IPSO)is proposed in this paper to realize the real－time online detection of cement kiln tail resolution ratio.IPSO－SVR is based on soft sensor measurement technique which solves the problem that some important industrial process parameters cannot be directly online measured.Adaptive inertia weight is introduced into PSO to avoid premature convergence and getting trapped in local extremum.The cement kiln tail resolution ratio soft sensor measurement model based on IPSO－SVR is built with the core parameter selection of SVR optimized by using IPSO.Simulation experiment proves that IPSO－SVR has a better forecasting ability compared with model based on SVR optimized by cross validation and PSOSVR.The correlation coefficient is 0.857 5.The maximum relative error is 1.14%，and the average relative error is 0.75%.It shows that IPSO－SVR can be further applied to the prediction of product resolution ratio in large scale industries such as cement production.

online detection;resolution ratio of kiln tail;soft sensor measurement;particle swarm algorithm;support vector regression machine

A

1674－5124(2016)11－0089－05

10.11857/j.issn.1674－5124.2016.11.019

2016－05－23;

2016－07－10

吉林省科学技术厅计划项目(20150203003SF)

金星(1976－)，男，吉林长春市人，副教授，主要研究领域为测控技术与智能系统。