GO法在惯导系统可靠性评估中的应用

胡爱玲，江秀红

(沈阳航空航天大学 电子信息工程学院，沈阳 110136)



GO法在惯导系统可靠性评估中的应用

胡爱玲，江秀红

(沈阳航空航天大学 电子信息工程学院，沈阳 110136)

摘要：GO法是一种以成功为导向的系统可靠性分析方法，可用来评估多状态、有时序、复杂系统的可靠性。采用GO概率公式算法，与故障树(FTA)法对比验证，研究了惯导系统(INS)基于GO法的可靠性分析与评估方法。阐述了GO法的具体分析步骤，构建了惯导系统的GO图模型，利用概率公式算法进行了可靠性的定量计算，并对系统中信号反馈的处理进行了初步探讨，给出了解决方案。最后与应用FTA的系统可靠性分析结果进行对比，证明了GO法在惯导系统这类产品中的应用是切实可行的。

关键词：可靠性分析；GO法；惯导系统；信号反馈；故障树法(FTA)

惯性导航系统(Inertial Navigation System,INS)是飞行器(飞机、导弹、卫星、火箭等)不可缺少的关键敏感部件，它可以保障飞行器姿态稳定、目标正确。惯导系统的安全性与可靠性将直接影响飞行任务的成败，因此其可靠性评估及建模方法一直是惯导科技工作者关注的主要研究方向[1-2]。

目前，在惯导可靠性和风险评价分析中，故障树(Fault Tree Analysis，FTA)是一种最常用的有效方法，如文献[3-7]针对惯导系统中比较常见的故障模式，均基于FTA提出了可行的故障诊断方案。然而FTA对复杂系统的建树有相当的困难，特别是不便于分析有多重状态的系统、有信号反馈的系统以及有时序功能变化的可维修系统等。

GO法是美国军方用于分析武器系统安全性和可靠性的一种有效方法[8]。对于有多状态、有时序的系统，尤其是有实际物流如气流、液流、电流产生的系统安全性分析更为适合。目前尚未见到GO法在惯导系统可靠性分析中的应用，本文将对其进行初步的研究。

1GO法的基本思想及分析步骤

1.1GO法基本思想

GO法最初由美国Kaman科学公司提出，近年来随着功能和算法的不断发展完善，在应用中表现出很多独特的优点，已在核电、设备性能分析、电网配电等领域得到成功应用[9-13]。

GO法的基本思想是把系统图或工程图直接翻译成GO图，GO图中用操作符代表具体的部件(或逻辑关系)，用信号流连接操作符，代表具体的物流(或逻辑上的进程)。GO法的分析方法主要有状态组合算法和概率公式算法。状态组合算法[10]需列出操作符和输入信号的全部状态组合计算联合概率，比较繁琐。概率公式算法[10,14]通过引入信号流状态累积概率，直接导出了GO操作符的计算公式，大大简化了定量计算。目前对于复杂系统，一般都采用概率公式算法。

1.2GO法分析步骤

利用概率公式算法进行定量计算的步骤如下：

Step1 建立GO图

进行系统功能分析，确定系统中各部件的操作符类型，建立GO图。

Step2 输入已知的可靠性数据

确定GO图中各操作符及输入信号的状态概率，一般用PS(i)、PC(i)、PR(I)表示输入信号、操作符及输出信号的状态概率，这里i= 0,1,…,N表示不同的状态值，0表示提前状态，N为故障状态，1～(N-1)表示多种成功状态(0～N也可代表有时序问题的多个时间点)。

Step3 定量计算

按信号流序列对每个操作符，按其类型相应的概率计算公式进行计算，直至得到代表系统输出信号的状态概率。

Step4 修正

若系统中含有共有信号，还需对Step3计算的结果进行修正，以获得更为精确的输出信号状态概率。

通过以上步骤即可完成系统的可靠性计算，输出信号的可靠性数值代表了整个系统稳定运行时的平均可靠性特性，据此可对系统做出评价，提出改进设计。GO法共定义了17种标准操作符，各操作符的概念及运算规则可见文献[10]。

2惯导工作原理及其GO图

为清晰地描述用GO法进行惯导系统可靠性分析的过程，以某平台惯导系统为研究对象，如图1所示。

图1　某三轴惯导系统基本结构原理图

平台惯导系统主要由以下几部分组成：(1)三个单自由度的陀螺和三个加速度计；(2)平台(含支架)；(3)直流力矩电机；(4)信号放大处理，包括前置放大以及功率驱动电路；(5)线性旋转变压器，作为角传感器，从方位环、俯仰环和滚转环上拾取环架角，也即飞机的航向角、俯仰角和滚转角；(6)导航计算机、数字控制器以及控制显示台；(7)电源及必要的附件等。

根据系统中各部件的功能及GO法中操作符的特点，以控制显示台输出有效的飞行加速度及姿态角信息为成功准则，将图1翻译成GO图，如图2所示。

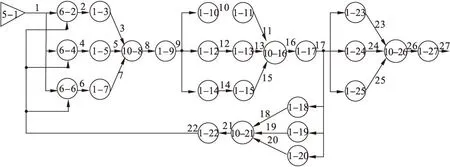
图2　某平台惯导系统的GO图

图2中各操作符的类型、代表的单元名称以及相应故障率按编号列于表1。为了与后面故障树分析结果进行对比，这里将所有操作符的状态都假定为2，也即操作符只有两个状态值，1为成功，2为故障，表1中的故障率即为状态值为2时对应的概率。

表1　惯导系统操作符数据

电源作为整个惯导系统的驱动动力，是系统的唯一输入，因此用单信号发生器(类型5操作符)代表；陀螺只有在接收到导航计算机的控制指令时，才能通过稳定回路控制惯导平台跟随系统所采用的坐标系，因此这里用有信号而导通的元件(类型6操作符)代表；前置放大、数字控制器、功率驱动电路、力矩电机、平台、旋转变压器、加速度计以及导航计算机、控制显示台都设定为两状态部件，用两状态单元(类型1操作符)代表；数字控制器只有在接收到陀螺的输出信号，才会通过电机控制架环的正确转动，三个陀螺的信息缺一不可，因此用与门(类型10操作符)代表几个信号之间的逻辑关系。同理，三个加速度计、三个电机以及三个旋转变压器的输出之间也用与门表示之间的逻辑关系。

3基于GO法的惯导可靠性分析

因该系统为两状态表示系统，为简便起见，用PCi表示第i个操作符的成功概率，同样用PSi和PRi表示第i个输入、第i个输出信号的成功概率。采用概率公式算法，沿信号流方向逐步计算，即可获得整个系统的成功概率。在计算之前，先对共有信号以及信号反馈进行解释，并给出解决方案。

3.1共有信号的处理

GO图中如果某信号流同时输入到多个操作符，则该信号称为共有信号。图2中，信号发生器1的输出同时输入到2、4、6三个操作符，它们的输出信号中都包含了信号1，因此信号1就是"共有信号"。对于具有多个输入信号的某些操作符(如类型2或门、类型10与门)，若多个输入信号中包含共有信号，那么利用概率公式计算得到的输出概率需要进行修正。

目前一般采用两种共有信号修正方法，一种是在输出信号的概率展开式中，直接将共有信号的高次项概率用一次项替代。比如输出概率PR=PS2PC，经修正后的正确输出概率为PR=PSPC。这种降阶方法必须推导出包含共有信号的信号流联合概率的表达式，对于有多个共有信号和多重逻辑门的复杂系统，表达式的推导和计算过程将变得很复杂。文献[15]在状态累积概率的基础上提出了一种解决思路，只要对共有信号的状态组合进行多次简单GO运算，就可得到输出概率的精确值，但此算法只针对具有两状态值的共有信号。对于本惯导系统，两种修正方法都可以用，这里为了更清晰的表达概率推导过程，将采用第一种方法进行修正。

3.2信号反馈的处理

图2中，一方面，信号2、4、6包含在信号17的输出表达式中；另一方面，信号17又反过来影响信号2、4、6的输出概率，这种现象即为信号反馈。目前还没有文献对GO图中的信号反馈给出合理的解决方案，一般都是直接将反馈断开，闭环变为开环，然后再沿信号流进行计算。这种处理方式在某些情况下是不影响最终结果的，比如图3(a)中的两状态系统，信号3反馈回来与信号1做与运算。无论是否考虑反馈，信号3的成功概率都为

PR3=PR1PC3

(1)

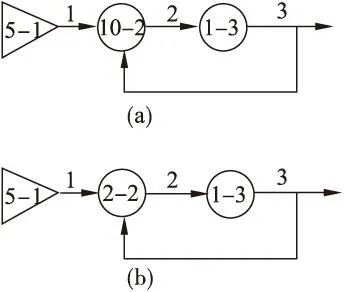
图3　信号反馈

但对于图3(b)中的两状态系统，信号3反馈回来与信号1做或运算。若只是简单的断开反馈通路，则输出信号3的成功概率为：

PR3=PR1PC3

(2)

而实际上，由逻辑关系可知，不论输入信号1的状态如何，只要操作符3成功，输出信号3即成功，所以输出概率表达式应为：

PR3=PC3

在这份集体合同中，劳动用工管理、劳动报酬及保险福利、劳动安全卫生、女职工和未成年工特别保护、职工培训等与从业人员息息相关的事项都被明确约定，今后，家政人员在工作中有了“护身符”，他们的权益将更有保障。

(3)

可见，简单的断开反馈通路，只考虑前向通路的逻辑计算不一定准确。针对两状态系统，这里提出一种通过建立方程求解输出概率的新方法。假设输出信号3的成功概率为x，则按照操作符的运算规则，对于图3(a)可得：

PR2=PR1x

PR3=PR2PC3=PR1PC3x=x

(4)

若要等式(4)成立，则只有x=PR1PC3，也即输出信号3的成功概率为PR3=PR1PC3。

对于图3(b)所示的或运算：

PR2=1-(1-PR1)(1-x)=x+PR1-PR1x

PR3=PR2PC3=(x+PR1-PR1x)PC3=x

(1-PC3+PR1PC3)x=PR1PC3

(5)

3.3基于概率公式的定量计算

下面利用概率公式算法对图2的惯导系统可靠性进行定量计算，由于存在反馈，假设信号流17的成功概率为x，则

①信号流22

PR22=(xPC18)(xPC19)(xPC20)PC22=PC18PC19PC20PC22x

②信号流8

PR8=(PR1PC2PR22PC3)(PR1PC4PR22PC5)(RR1PC6PR22PC7)

=PR1PC2PC3PC4PC5PC6PC7PR22

③信号流16

PR16=PR8PC9(PC10PC11)(PC12PC13)(PC14PC15)

=PR8PC9PC10PC11PC12PC13PC14PC15

④信号流17

PR17=PR16PC17=x

所以PR17=x=PR1PC2PC3PC4PC5PC6PC7PC8PC9PC10PC11*PC15PC17PC18PC19PC20PC22

⑤信号流27

PR27=PR17PC23PC24PC25PC27

=PR1PC2PC3PC4PC5PC6PC7PC9PC10PC11PC12PC13PC14*PC15PC17PC18PC19PC20PC22PC23PC24PC25PC27

将表1数据代入，可得：

PR27=0.999238

这即为控制显示台能正常输出信息的成功概率。

4与FTA法惯导可靠性对比分析

为验证上述分析过程的有效性，采用FTA对惯导系统进行可靠性计算，以控制显示台不能输出正常的飞行加速度及姿态角为顶事件，建立故障树如图4所示。假设各事件相互独立，对应的名称及故障率如表2所示。

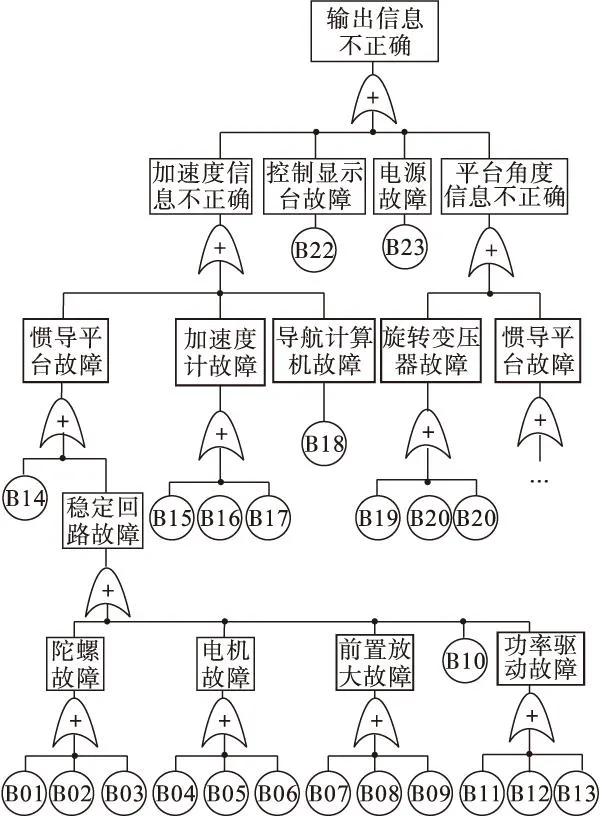
图4　惯导系统的FTA图

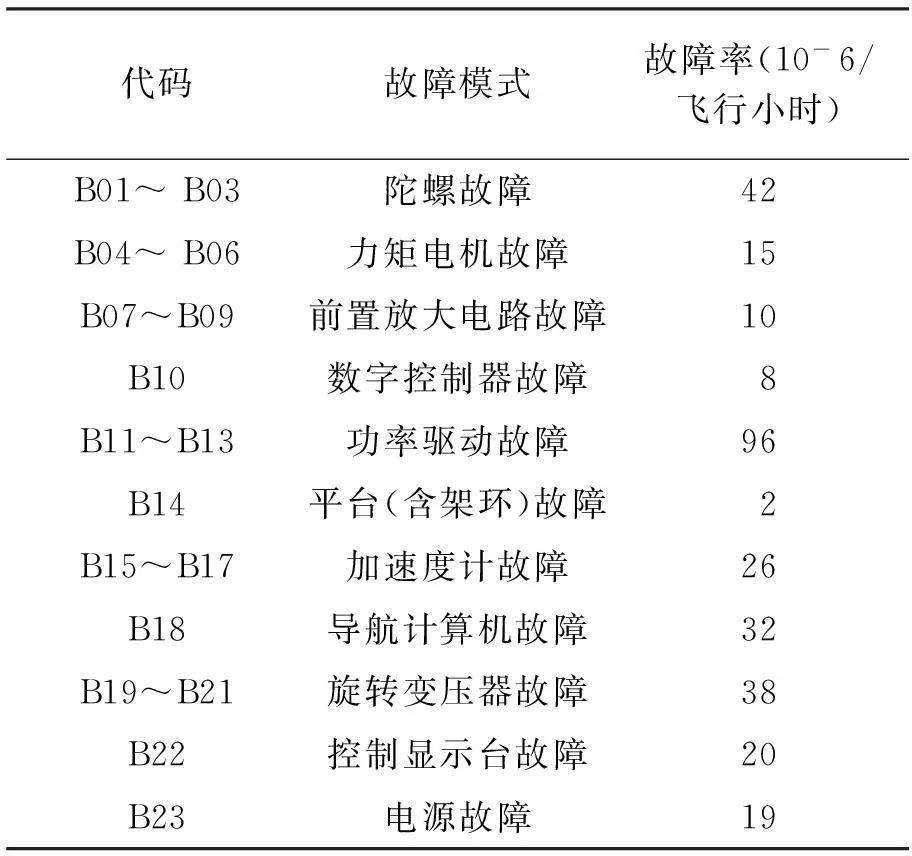
代码故障模式故障率(10-6/飞行小时)B01～B03陀螺故障42B04～B06力矩电机故障15B07～B09前置放大电路故障10B10数字控制器故障8B11～B13功率驱动故障96B14平台(含架环)故障2B15～B17加速度计故障26B18导航计算机故障32B19～B21旋转变压器故障38B22控制显示台故障20B23电源故障19

由故障树顶事件的计算方法可得：

(6)

式中，λi为第i个事件发生的概率，λ为顶事件发生的概率。将表2数据代入，可得：

λ=0.000762

又1-0.000762=0.999238，与GO法分析的结果相同，证明采用GO法进行惯导系统可靠性分析是切实可行的。

为了与FTA方法进行对比，图2中GO图进行了大量简化，比如设定系统为两状态系统。但实际上，系统中的陀螺、加速度计等都属于敏感元件，一些外界的干扰刺激等都会引起输出信号的发生，因此在GO图中，触发发生器(类型3，具有3个状态值)更适合代表它们；还有针对系统中存在的机械延时、电子系统延时响应以及操作员的响应等，还应考虑在系统中加入延时发生器(类型8操作符)。因此为了更准确地对系统进行可靠性评估，在系统GO法建模上还要考虑更多的因素，而这些多状态、信号反馈以及延时等都是传统FTA法解决不了的问题。因此GO模型在模拟实际工作状况方面比FTA具有更大的优势，GO法计算的可靠度信息与FTA相比会更加精确。

5结论

(1)由于惯导系统可靠性评估所需要的一些基础数据的统计还不完善，为了与FTA法作对比，在GO法的分析过程中对一些元件的数据进行了假设。

(2)由于GO法自身的特点与优势，近年来逐步受到重视和发展。本文研究了GO法在惯导系统可靠性定量评价中的应用问题，通过与采用FTA对惯导系统进行定量分析结果的比较，证明了GO法在惯导系统可靠性分析中的可行性与正确性。

(3)与FTA方法相比，17种GO操作符的灵活组合，使GO法可以更好地对多状态、有时序、有反馈的系统进行可靠性建模，可以与实际工作状况更加相符，因此GO法在系统建模、定量算法等方面具有很大的优势和发展潜力。

参考文献(References)：

[1]LI HONG-BO,HAO YAN-LING.Risk assessment model of ship integrated navigation system based on fuzzy artificial neural network[C].International Conference on Computational Intelligence and Security,2010:425-428.

[2]TAUFER J,BAZANT L.The risk analysis of pseudolite and satellite navigation system[C].2nd International Conference on Safety and Security Engineering,2007:19-17.

[3]KHANH NGUYEN T P,JULIE BEUGIN,JULIETTE MARAIS.Method for evaluating an extended fault tree to analyse the dependability of complex systems:Application to a satellite-based railway system[J].Reliability Engineering and System Safety,2015,133:300-313.

[4]刘晨曦,陈南,杨佳宁.基于多态故障树的伺服刀架可靠性分析[J].东南大学学报,2014,44(3):538-542.

[5]SONG HUA,ZHANG HONG-YUE,CHAN C W.Fuzzy fault tree analysis based on T-S model with application to INS/GPS navigation system[J].Soft Computing,2009:31-40.

[6]武文斌,汪立新,周小刚,等.基于改进的动态故障树的惯导系统安全性分析[J].航天控制,2011,29(5):63-66.

[7]张志鑫,张峰.基于故障树和奇异值分解的捷联惯导系统故障检测[J].中国惯性技术学报,2008,16(3):359-363.

[8]CHUN B B.GO methodology:overview manual[R].EPRI NP-3123,Vol.1,Electric power research institute,1983.

[9]李哲，鲁宗相，刘井泉.基于GO法的核电厂电气主接线系统可靠性分析[J].核动力工程,2010,31(3):69-73.

[10]沈祖培,黄祥瑞.GO法原理及应用——一种系统可靠性分析方法[M].北京：清华大学出版社,2004.

[11]金霞,段富海.基于GO法的电动静液作动器可靠性分析[J].大连理工大学学报,2013,53(6):846-850.

[12]龚剑波,黄民翔,孙飞飞.基于GO法的含分布式电源的配电系统可靠性评估[J].电力系统保护与控制,2012,40(16):90-94.

[13]刘林林,任羿,王自力,等.基于贝叶斯网络的GO法模型算法[J].系统工程与电子技术,2015,37(1):212-218.

[14 ]SHEN ZUPEI,GAO JIA,HUANG XIANGRUI.A new quantification algorithm for the GO methodology[J].Reliability Engineering and System Safety,2000,67(3):241-247.

[15]SHEN ZUPEI,GAO JIA,HUANG XIANGRUI.An exact algorithm dealing with shared signals in the GO methodology[J].Reliability Engineering and System Safety,2001,73(2):177-181.

(责任编辑：陈素清英文审校：刘红江)

Application of GO methodology on reliability assessment of the inertial navigation system

HU Ai-ling,JIANG Xiu-hong

(College of Electronic and Information Engineering,Shenyang Aerospace University,Shenyang 110136,China)

Abstract：GO methodology is a success-oriented system reliability analysis technique,which can analyze and assess the reliability of multi-state,related-time,complicated systems.This is the first attempt to apply GO methodology in the reliability analysis of Inertial Navigation System (INS).GO probability formula algorithm and comparison with Fault Tree Analysis(FTA) method are used.Concrete steps of GO methodology are discussed,GO model of INS is built,and the quantification calculations are processed using probability formula algorithm in GO methodology.Besides,primary discussion for signal feedback is progressed and a solution is provided.Finally,through the comparison of the results of the GO and FTA method,it proves that the application of GO methodology in INS is valid and feasible.

Key words：reliability analysis;GO methodology;INS;signal feedback;fault Tree Analysis (FTA)

doi:10.3969/j.issn.2095-1248.2016.01.011

中图分类号：TB114.3

文献标志码：A

文章编号：2095-1248(2016)01-0054-06

作者简介：胡爱玲(1978-)，女，硕士，讲师，主要研究方向：航空电子系统，系统可靠性分析及在线故障诊断等研究工作。Email:alhu@sau.edu.cn

收稿日期：2015-10-13