巧用三角函数公式解题

于真灵



巧用三角函数公式解题

于真灵

三角函数公式包括同角三角函数的基本关系式、诱导公式、两角和与差的正弦、余弦和正切公式、二倍角的正弦、余弦、正切公式、辅助角公式。公式多但有规律，把握其规律，在解题中就能灵活运用。教师在教学中应注重引导学生掌握规律，切实提高学生的解题能力。

一、三角函数公式的正用

1.思路方法：分析结构特点，选择恰当公式；利用公式化成单角三角函数；整理得到最简形式。

2.化简要求：化简过程是恒等变形；结果要求项数尽可能少，次数尽可能低，结构尽可能简单，能求值的要求出值。的值。（1）求

2.三角函数的给值求值，关键是把待求角用已知角表示：已知角为两个时，待求角一般表示为已知角的和或差；已知角为一个时，待求角一般与已知角成倍的关系或互余互补的关系。在求值的过程中，“拼凑角”对求值往往起到峰回路转的效果，因此可以利用所给条件适当地进行拆角、凑角。常见的变角技巧有琢+茁=渊琢-茁冤-渊琢-茁冤，琢＝222（琢－茁）＋茁，仔+琢=仔-渊仔-琢冤，15毅越45毅原30毅等。424

二、三角函数公式的逆用

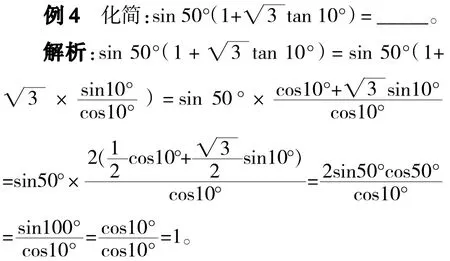
三、三角函数公式的变用

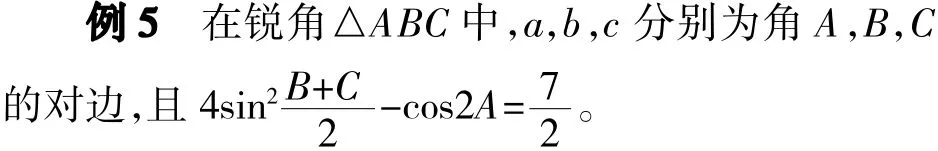
（1）求角A的大小；（2）求sinBsinC的最大值。

四、三角函数公式在解三角形中的应用

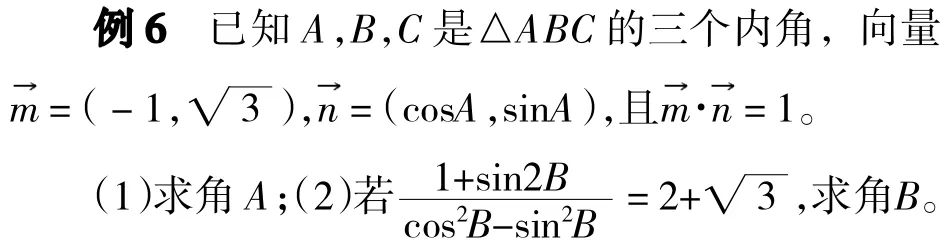
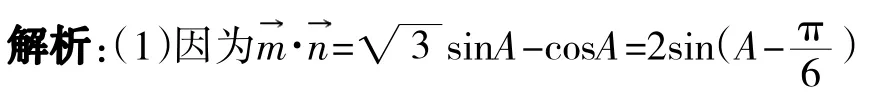
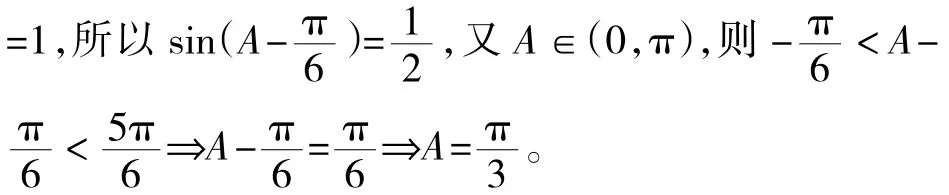
2.求角时，通常是先求出该角的某一个三角函数值，再结合其范围确定该角的大小。

巧用三角函数公式，应掌握“三种方法、两个技巧、三个变换”。

“三种方法”是指三角函数求值与化简的常用方法，主要有弦切互化法：利用公式化成正、余弦；和积转换法：利用的关系进行变形、转化；巧用“1”的变换

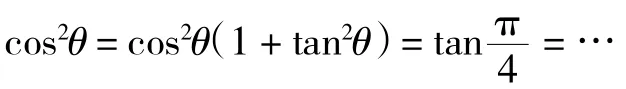
“两个技巧”是指拼角、凑角的技巧，包括：（1）用已知角表示未知角等；（2）互余与互补关系

“三个变换”是指应用公式解决问题的三个变换角度，主要有（1）变角：目的是沟通题设条件与结论中所涉及的角，通常是配凑；（2）变名：通过变换函数名称达到减少函数种类的目的，通常有切化弦、升幂与降幂等；（3）变式：根据式子的结构特征进行变形，使其更贴近某个公式或某个期待的目标，通常有：常值代换、逆用变用公式、通分约分、分解与组合、配方与平方等。

（作者单位：绥宁县第一中学）

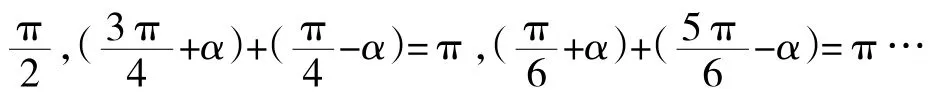
探索