例谈中学数学思想与方法的渗透

潘玉琦



例谈中学数学思想与方法的渗透

潘玉琦

教学案例：比较二次根式的大小。

师：我们知道，两个正数里，较大的正数的平方也较大，它们的算术平方根是否也具有相同的规律呢？这个问题，大家动手算一算。

学生小组合作，边计算，边探讨。教师将两个小组的计算结果用投影仪展示。

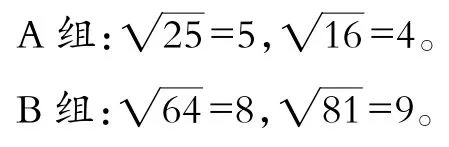
师：请同学们仔细观察这两组的结果，你发现了什么？

生1：我发现正数越大，它的算术平方根就越大。

生2：我发现两个正数的算术平方根进行比较，大数的算术平方根大于小数的算术平方根。

师：这个结论是不是带有普遍性呢？我们再用几个其他的数试一试。

学生尝试归纳，教师总结：一般地，当a＞0，b＞0时，如果a＞b，则有

上述教学案例中，学生通过动手计算，考察了部分正数的算术平方根的大小关系后，用不完全归纳法得出了结论：一般地，当a＞0，b＞0时，如果a＞b，则有

正如案例中所体现的一样，数学思想与方法往往隐含在知识里，体现在知识的发生、发展过程。实践证明，在课堂中渗透数学思想与方法，能使学生快速掌握知识的内涵，提高学生的数学素养。那么如何渗透呢？

在知识的发生过程中渗透。数学教学内容从总体上可分为两个层次：一个称为表层知识，包含概念、性质、法则、公式、公理、定理等基本内容；另一个称为深层知识，主要指数学思想与方法。表层知识是深层知识的基础，具有较强的操作性。学生只有通过对教材的学习，在掌握与理解一定的表层知识后，才能进一步学习和领悟相关的深层知识。而数学思想与方法又是以数学知识为载体，蕴含于表层知识之中，是数学的精髓，支撑和统率着表层知识。教师在讲授概念、性质、公式的过程中，应不断渗透相关的数学思想与方法，让学生在掌握表层知识的同时领悟到深层知识，从而使学生的思维产生质的飞跃。只讲概念、定理、公式而不注重渗透数学思想与方法的教学，将不利于学生对所学知识的真正理解和掌握，使学生的知识水平永远停留在初级阶段，难以提高。在教学过程中，教师可以引导学生主动参与结论的探索、发现、推导过程，搞清其中的因果关系，领悟它与其他知识的关系，让学生亲身体验创造性思维活动中所经历和应用到的数学思想与方法。

在问题的探索、解决过程中揭示。我们的教学一直存在这么一个现象：题目讲得不少，可只要条件稍作改变，一些学生就会不知所措，总是停留在模仿型解题的水平上，很难形成较强的解决问题的能力，更谈不上创新能力的形成。这主要是由于教师没有将题目所蕴含的数学思想与方法予以揭示。在教学解决问题的过程中，教师应把最多的精力花在诱导学生怎样去想，怎样想到，到哪里去找解题的思路上，要将数学思想与方法的运用置于解题教学的中心位置，充分发挥数学思想与方法的解题功能——定向功能、联想功能、构造功能和模糊延伸功能。若学生能在解决问题的过程中充分发挥数学思想与方法的解题功能，不仅可少走弯路，还可大大提高数学能力与综合素质。

（作者单位：安徽省滁州市第八中学）

探索