一道有理函数不定积分题目的多种计算方法

刘春辉

（赤峰学院　数学与统计学院，内蒙古　赤峰　024001）



一道有理函数不定积分题目的多种计算方法

刘春辉

（赤峰学院数学与统计学院，内蒙古赤峰024001）

摘要：本文综合运用有理函数积分法以及多种方式的换元积分法，给出了一道不定积分题目的多种计算方法，开拓了不定积分的解题思路.

关键词：不定积分；有理函数积分法；换元积分法

不定积分的计算是高等数学[1-3]课程的一项重要的内容，通常的高等数学教材中都是通过依次介绍换元积分法、分部积分法和有理函数的积分法三个板块来编排教学内容的.但学生在学习完这部分内容后，往往会遇到一个十分令人困惑的问题，那就是，面对一道不定积分的计算问题，如何去选择一个适当的方法计算出其结果？事实上，对于各类积分法不应该将他们孤立的去看待，而应该将他们看成为一个相互影响的有机整体，进而从中分别体会每类方法的精髓.计算不定积分的过程是一个灵活多变的过程，大多情况下，对一个不定积分的计算常常需要综合运用多种方法.同时，对同一问题，用不同的视角去分析，从而得到多种不同的解题思路，有助于不断积累解题经验，提高解题效率.鉴于此，本文将以一道有理函数的不定积分计算题目为例，运用多种方法给出其计算过程.

解法1从被积函数的形式上来看，它是一个典型的有理函数.因此，最常规的方法，也是最容易被想到的方法就是按照有理函数积分法进行计算.从而有：

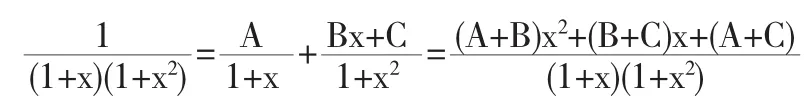
比较分子的系数，得关于待定系数A,B,C的方程组

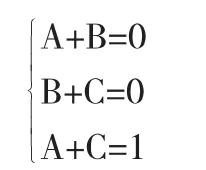
解之得

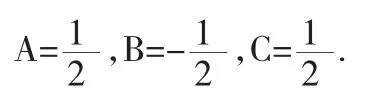
故

因此，我们有

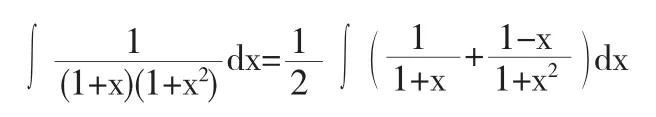
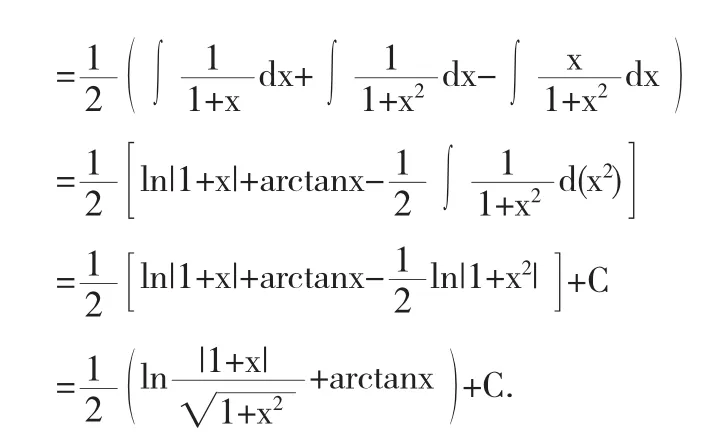
令1+x=t，则1+x2=1+(t-1)2=t2-2t+2，dx=dt，从而原积分变形为：

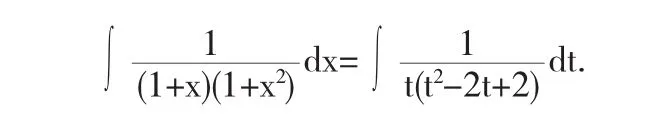
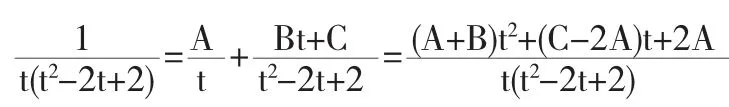
比较分子的系数，得关于待定系数A,B,C的方程组

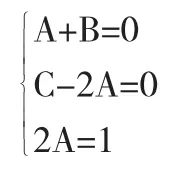
解之得

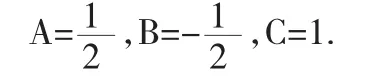
故

因此，我们有

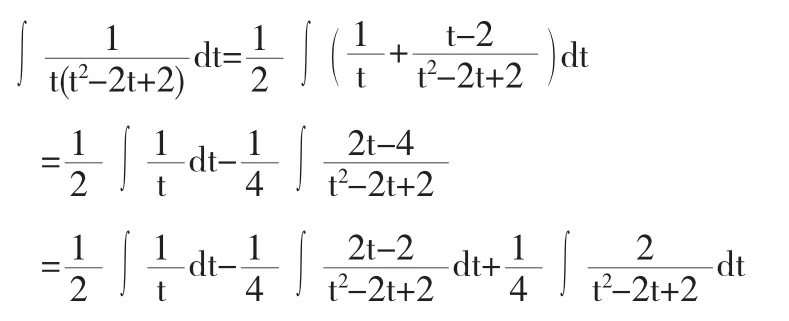
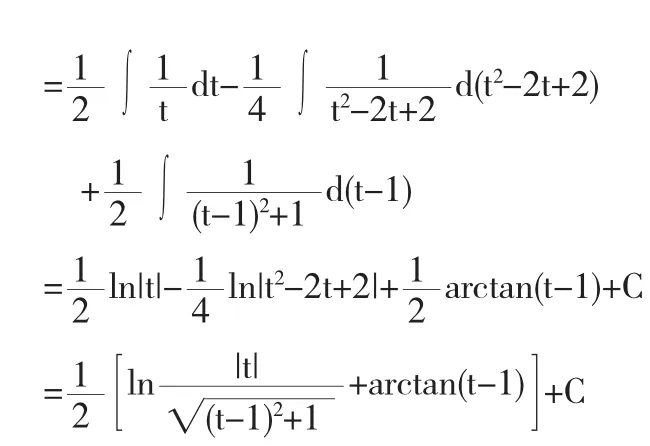
将t=1+x带入上式，便得

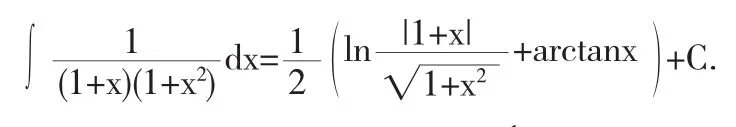
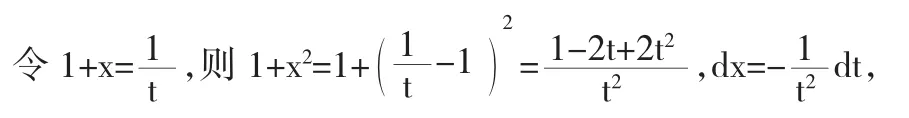
从而原积分变形为：

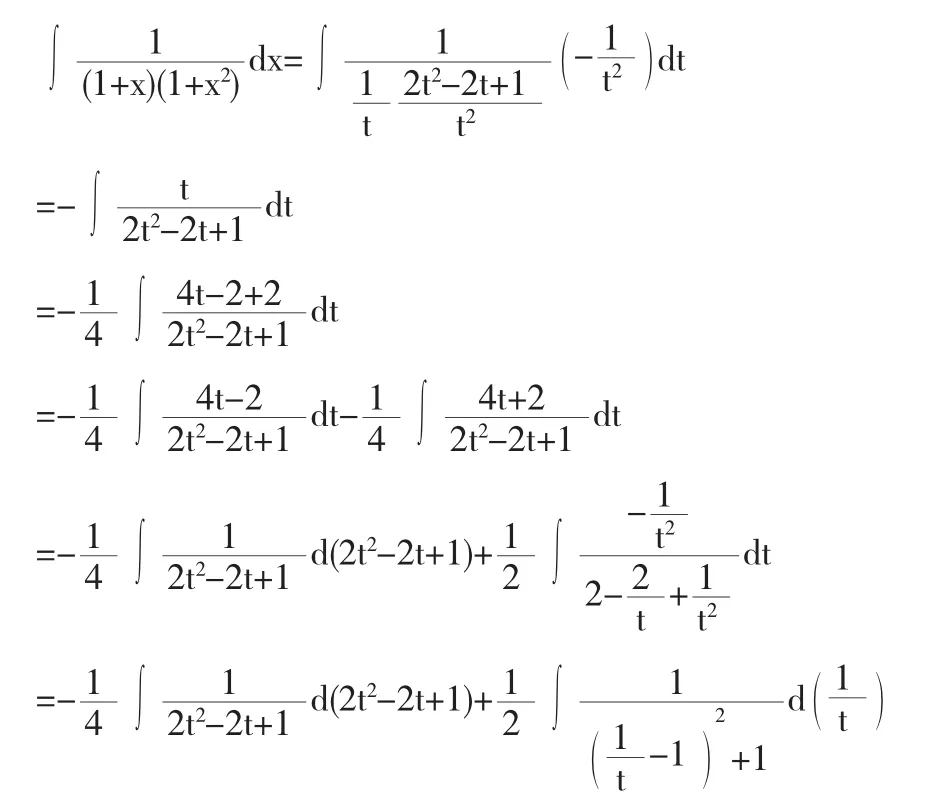
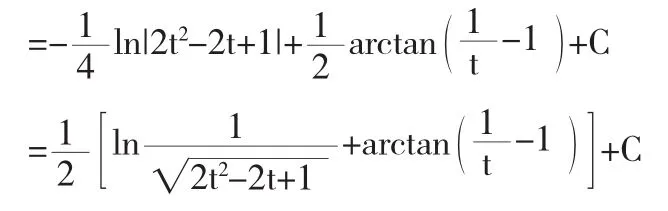
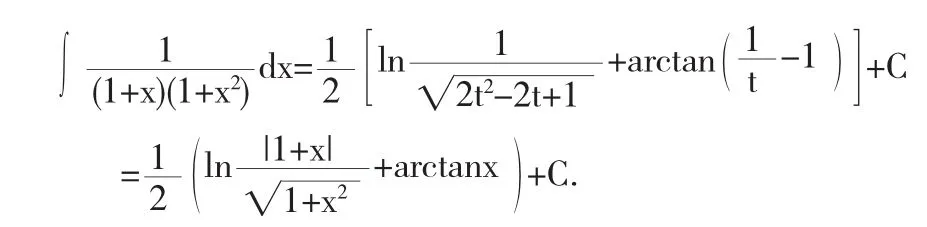
注意到被积函数中包含1+x2，针对这一特点，可以考虑利用三角恒等式

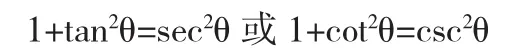
进行三角换元.鉴于大多数高等数学教材中都利用前者进行换元，这里我们利用后者进行讨论.于是有：

解法4令x=cotθ，则dx=-csc2θ，于是

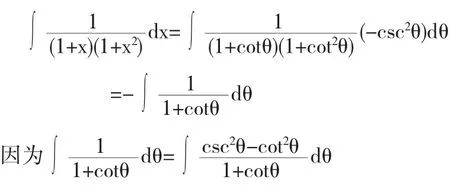
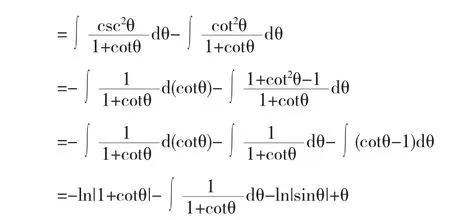
所以，移项得

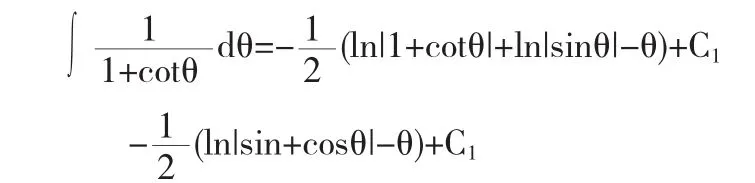
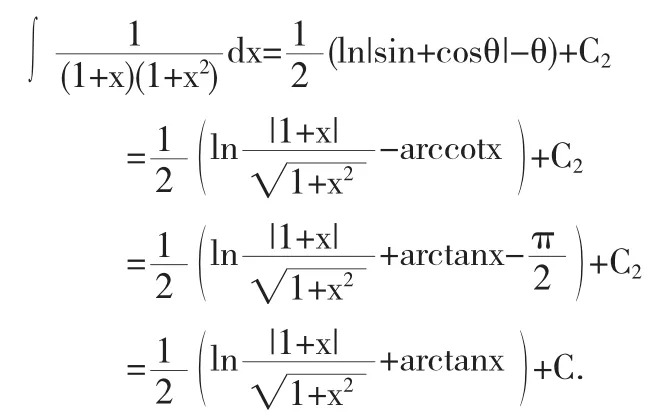
解法5令x=cotθ，则dx=-csc2θ，于是

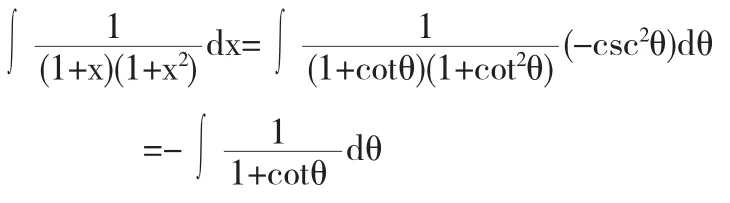
因为

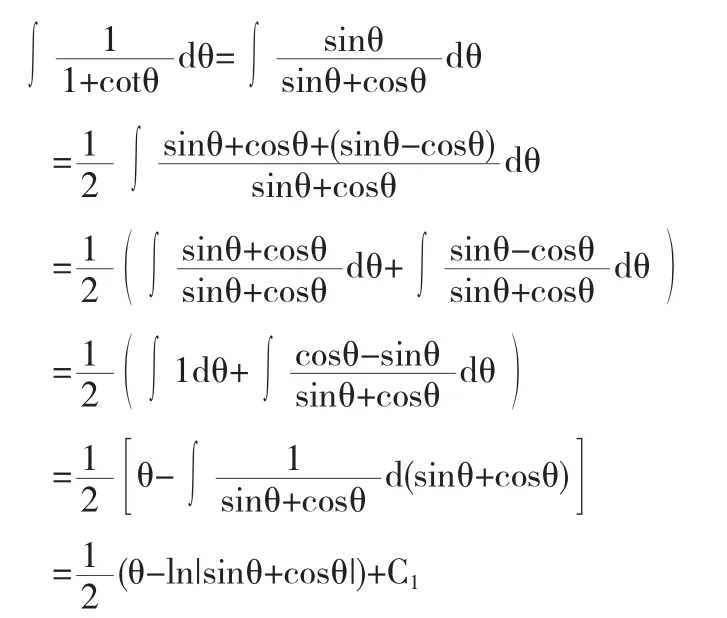
所以，结合解法4的变量回带过程得

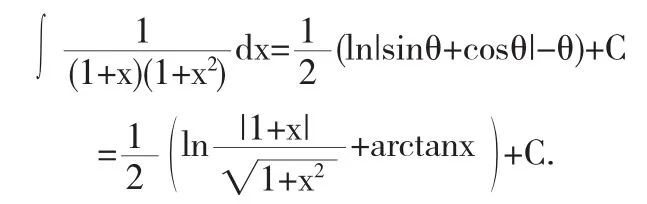
解法6令x=cosθ，则dx=-csc2θ，于是

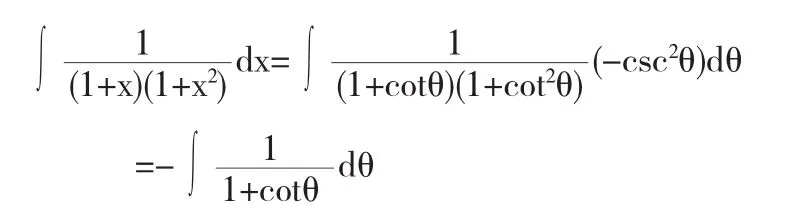
因为

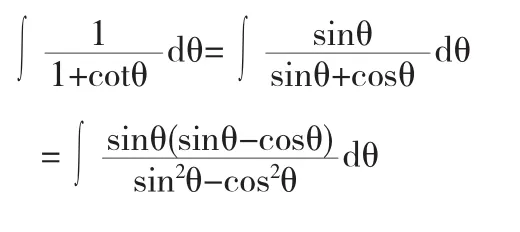
所以，结合解法4的变量回带过程得

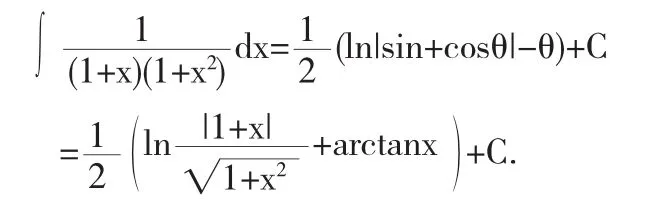
解法7令x=cotθ，则dx=-csc2θ，于是

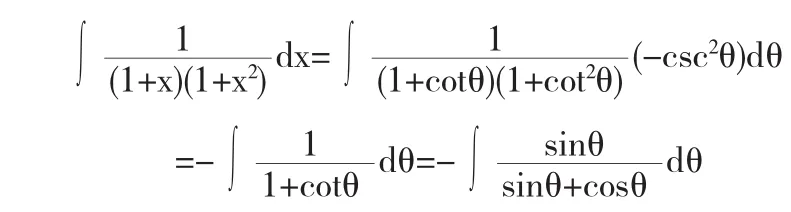
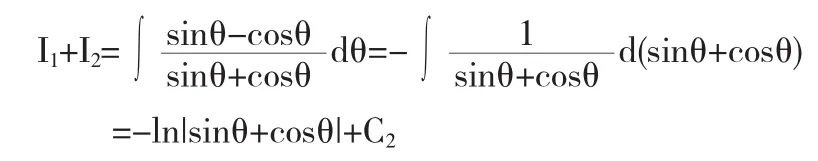
所以

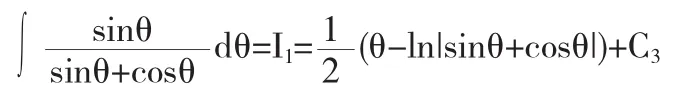
因此，结合解法4的变量回带过程得

解法8令x=cotθ，则dx=-csc2θ，于是

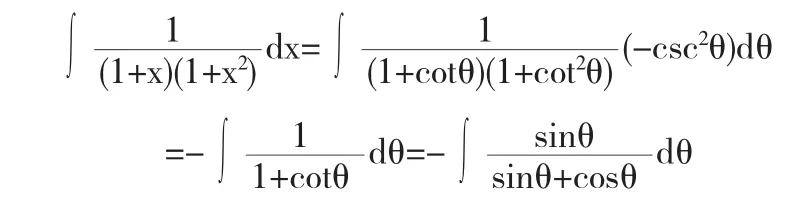
因为

所以，移项整理得

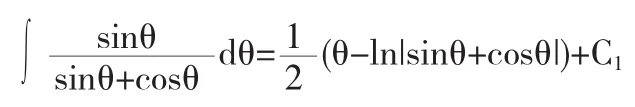
因此，结合解法4的变量回带过程得

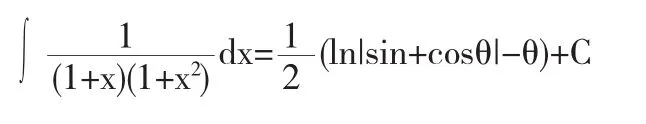
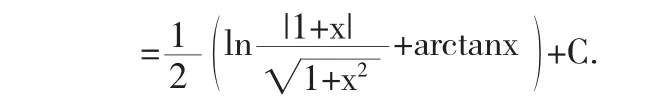
解法9令x=cotθ，则dx=-csc2θ，于是

因为

所以，结合解法4的变量回带过程得

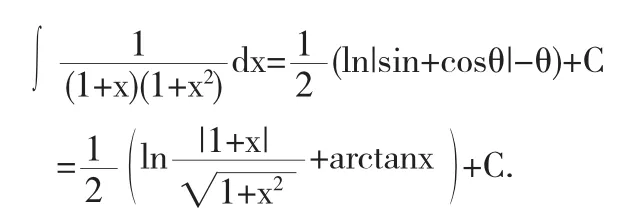
结束语

通过上述讨论，我们给出了一个不定积分的9种计算方法，细心的读者不难发现，如果在解法4-9中采用x=tanθ的方式换元，还可以得到类似于解法4-9的6种方法，因此，实际上我们给出了该不定积分的15种计算方法.虽然15种方法考虑问题的角度与出发点各不相同，但是殊途同归，最终获得的结论是一致的，这正是数学问题一题多解的精髓所在.问题的讨论过程，不仅可以让我们不断开拓思维，使思考问题的思路更加灵活，做到“举一反三”，而且有助于我们进一步理清前后知识的脉络，达到融会贯通的效果.

参考文献：

〔1〕同济大学数学系.高等数学：上册[M].北京:高等教育出版社,2014.

〔2〕同济大学数学系.高等数学附册：学习辅导与习题选解[M].北京:高等教育出版社,2014.

〔3〕同济大学数学系.高等数学习题全解指南上册[M].北京:高等教育出版社,2014.

收稿日期：2015年10月9日

中图分类号：O172

文献标识码：A

文章编号：1673-260X（2016）02-0001-03