减法，让问题变简单

◆马云聪

(河北乐亭县第一中学)

减法，让问题变简单

◆马云聪

(河北乐亭县第一中学)

通过学习经验，论证在做数学题时适当做做减法，让图形变得简洁些，对于定理中条件的要求就能认识得更充分些。阐述了“减法，让问题变简单”的道理，供大家探讨。

数学 减法 问题 简单

在利用线面平行的判定定理证明平行的图形，发现PC这条直线是联系MN和平时，由于不能很快找到面内的平行直线，让面PAD的纽带，由直线PC和MN会形成很多同学颇为苦恼。经过一段时间的探索，我发现了一个比较有趣的方法，让我在证明线面平行的相关问题时，能够很快地找到平行直线。这还要从笔者解一道课本题说起：

如图1所示，在四棱锥P-ABCD中，M，N分别是PC，AB的中点，若ABCD是平行四边形，求证：MN∥平面PAD。

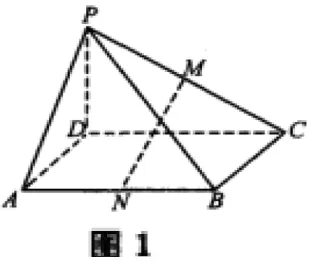
在本题中，要想证明MN∥平面PAD，就需要在平面PAD内找一条

线与MN平行，题目所给的图形中，有些线是多余的，那么我们去掉多余的线，是不是方便我们更好地看图呢？

我们去掉多余的线，就形成如图2所示的图形，发现PC这条直线是联系MN和平面PAD的纽带，由直线PC和MN会形成一个平面，这个平面与已知平面PAD有一个交点，根据公理可以知道这两个平面一定有一条交线，同时，点N，C和直线AD共面，所以连结直线NC，那么直线NC与AD有一个交点，设为E，就形成了图3．连结线段PE，这时我们会感觉到直线 MN和PE是平行的。那么，下面我们就要想办法证明MN∥PE，这个问题的证明就简单了。

小刚听了我的分析，觉得图形变简单了，因为一些在证明过程中不重要的线和面没有了，把问题的矛盾集中体现出来了，容易去作辅助线或者辅助面了，很好，但又不是很确定，所以，他给我出了道题，想看看，我还能够用这个方法来解决吗？

如图4，已知斜三棱柱ABC—A1B1C1中，AB—AC，D为BC的中点。

求证：AlB∥平面ADC1。

要证AlB∥平面ADC1，先把图形简化成图5，显然只要连结A1C，交AC1于点M，连结DM，如图6．这样DM就是平面ADC1中，与AlB平行的直线。

当我给出辅助线，并给出证明时，小光还没有找到辅助直线，顿时佩服不已。“我也在用你的思路啊，为什么我没有找到这样的辅助线啊？”小光说出了自己的困惑，并让我看了他的简化图7。

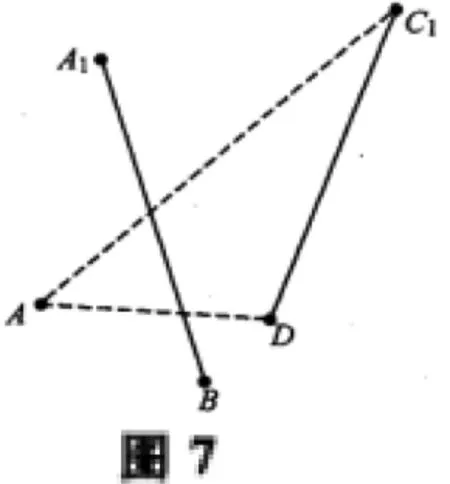
我看到小光的简化图，就知道原因了。原来小光的简化图，减去的线段太多了，最糟糕的是，小光把联系AlB和平面ADC1的纽带BC这条线也去掉了。显然，我的方法主要是减去图形中无用的线条，对于联系要证明关系的元素之间的纽带是必须保留的，而且是关键元素。

听了我的讲解，小光似乎抓住了重点，便求着我给自己出道题，让自己好好做做，看看是否真会了。小光做出来之后，很高兴，感觉这个方法最大的好处在于，通过减少线条，使需要证明的元素之间的关系显得更突出，从而找平行线时，思路就明显了。