基于优化的BP神经网络学生学习状态指数的评价研究

◆赵智鹏 高艳梅 赵寅旭 王 巍

(1.德惠市校外教育指导中心；2.德惠卫生职工中等专业学校；3.大连民族大学计算机学院)

基于优化的BP神经网络学生学习状态指数的评价研究

◆赵智鹏1高艳梅1赵寅旭2王 巍3

(1.德惠市校外教育指导中心；2.德惠卫生职工中等专业学校；3.大连民族大学计算机学院)

随着教学内容和教学模式方法不断改进，学生为教学主体的理念逐步深化。有效的掌握学生学习状态，能够有效提升教学效果。如何评价学生主体的学习状态，成为教师关注的重点。算法采用经附加动量和自适应学习速率优化后的BP神经网络(Back-Propagation Network)进行学生学习状态指数评价。实验结果表明参与评价的在校学生的整体学习状态较好，影响其学习状态的的主要因素是学习计划的有效执行，课前课后主动复习和预习、自信乐观程度、当前学习成绩等。

教学模式 BP神经网络 自适应学习速率

一、问题背景

随着目前教学研究内容的逐步细化，教学模式和教学方法也在不断改进。翻转课堂教学模式，行为导向教学法、案例教学法、任务驱动教学法等，这些教学方式的实施前提都是以学生为主体，以此提高教学效果。教学效果的评价可以通过历年考试或成绩评定，那么如何评价学生学习态度、学习主动性方面的进步，调动学生学习积极性，让学生参与到教学活动中来，注重课前预习，提高学生的自主学习，自我管理能力，让学生意识到自己是教学的主体，这才是提高教学效果的根本。本文研究如何进行学习状态指数评价的问题。以统计分析调查问卷的方式来研究该指数。通过已有调查问卷的结果的分析，确立了评价在校学生学习状态的18个指标。调查问卷的每个问题和每个指标一一对映，对学生学习态度进行正确的评价。

在目前常用的评价模型中，层次分析法(Analytic Hierarchy Process，简称AHP)是将与决策总是有关的元素分解成目标、准则、方案等层次，在此基础之上进行定性和定量分析的决策方法。采用层次分析法定量数据较少，定性成分多，评价结果说服力不强； BP神经网络的优势在于其可以实现复杂的非线性映射并且具有较强的泛化能力，学习能力强，受人为和新增数据影响小，其结果的准确性和可靠性使得评价鲁棒且有效。本文采用优化的BP神经网络对学生学习状态指数进行评价。

二、评价体系的建立

1.“5分制”标准

规定调查问卷中各题的每个选项的分值为自然数1、2、3、4、5，选项含义越积极分值越大。

2.评价指标确立

问卷调查部分统计信息结果会在实验部分指出。

经过进一步讨论与总结，将影响学生学习状态的指标归为以下十八项：

学习活动因素包括如下(T的下标排序与问卷题号顺序对应)：

在学习过程中有自己的学习计划、每天的课程学习时间、每周题库登陆次数、每周完成题库题目数量、每周在线学习平台学习时长、关注老师发布的教学内容、愿意主动和老师进行交流、愿意和同学进行交流、小组合作提高了学习效率和学习进度、在课前和课后主动预习和复习、对目前教学方式满意。

例如，在每日学习过程中能执行自己的学习计划吗(限选一项)

没有计划……………………l

偶尔有……………………2

有计划，但执行力差……………………3

能基本执行计划…………………………4

严格执行计划…………………………5

以下问题讨论非学习活动因素对学生学习状态的影响：

和老师的关系，和同学的关系、自信乐观程度、经济压力、学习成绩、业余生活、自身健康。

上述18个指标随机分布，分别用T1到T18表示。

经过调研，以上十八个指标影响着学生个体的学习状态指数。对于每个被调查的个体而言，他的最终结果T取决于他在T1到T18中的选择结果，而一个总体的指数，取决于每个个体的贡献值，在BP神经网络的输入中所有的输入值都向T的值靠拢，T的值为用户回答问题(即认为自己的学习状态如何)所得的分值。因此，可以指出T1到T18十八个指标能够体现总体的学习状态指数。

三、模型的建立与求解

1.模型的建立

(1)BP神经网络

反向传播网(Back-Propagation Network，BP网络)是将由威德罗和霍夫提出的W-H学习规则一般化，对非线性可微分函数进行权值训练的多层网络。BP神经网络的学习过程采用误差反向传播算法，它是一个有监督的神经元网络学习算法。

(2)附加动量法

针对于BP网络存在局部极小值的情况，利用附加动量的作用则有可能滑过局部极小值。如式3所示。

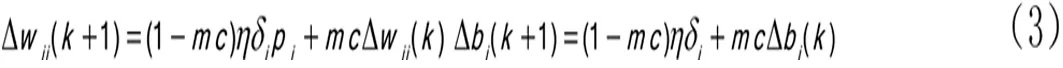
(3)自适应学习速率

自适应学习效率是指在神经网络的训练过程中，为了避免陷入局部最小解，根据训练集的实际收敛状况动态调整学习速率。

根据评测取得的26份调查问卷，将其中调查问题Q1到Q18的相应数据构造矩阵P26×18，矩阵P的每一行即为每份问卷的指标向量。用问题Q1的答案构造与P对应的输出向量Out。

2.神经网络的训练与使用

(1)神经网络的初始化

根据神经网络设置规则，并通过反复实验，本文算法将第一层神经元个数设为18，对应的输入向量为本文确定的18个评价指标的分值，隐含层神经元个数设为5，输出向量为5维向量，表示该问卷的学生学习状态指数等级。

第一层的激活函数为正切S型函数，第二层为线性激活函数，有监督的学习方式采用梯度下降动量和自适应学习率的BP算法。

(2)神经网络的训练

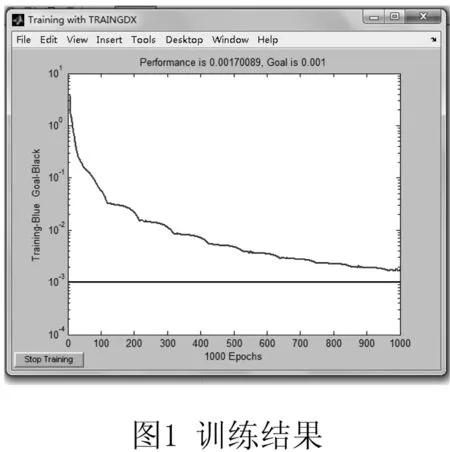
在训练过程中迭代次数设为1000，误差值是0.001，学习速率为0.01，学习速率增长上限为1.05，增长下限为0.7，训练结果如图1所示。

(3)神经网络计算

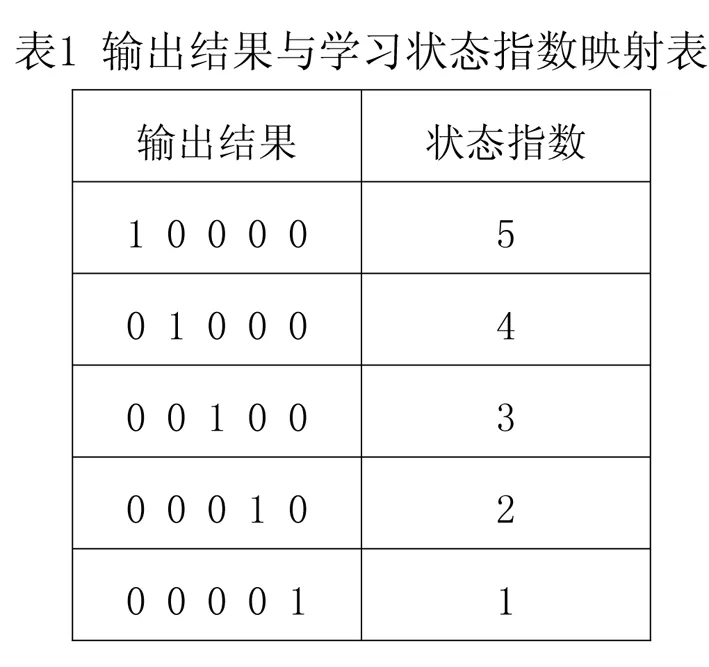
使用已经训练好的神经网络，对P矩阵进行每一行的神经计算和识别，并将计算结果归一化。输出结果与学生学习状态指数的映射关系如表1所示：

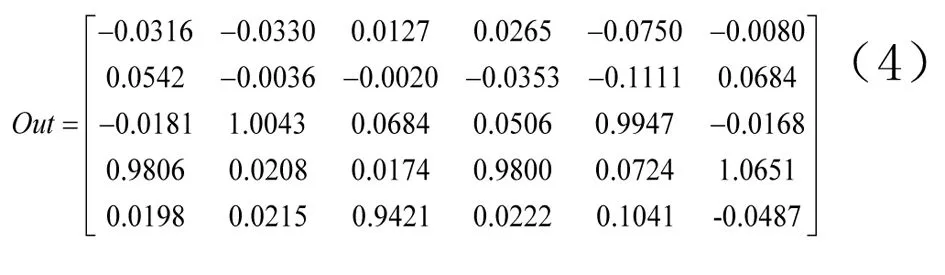
从调查问卷中随机取出6个样本P6、P20、P15、P3、P16、P4作为测试数据，其余20个作为训练样本。通过模型计算得输出矩阵如式4所示。

通过神经网络计算后返回的各指标权重为W其对应关系如下，T、W两个向量按顺序一一对应。

T={关注老师发布的教学内容，每周题库登陆次数，和同学的关系，愿意和同学交流学习，小组合作提高了学习效率和学习进度，每周完成题库题目数量，愿意主动和老师进行交流，在课前和课后主动预习和复习，自身健康，经济压力，对目前教学方式满意，每周在线学习平台学习时长，自信乐观程度，和老师的关系，每天的课程学习时间，学习成绩，学习过程中有学习计划，业余生活}

W={0.2373，0.1746，0.5613，0.3693，-0.2270，0.0614，0.2186，-0.7524，0.6202，0.5122，-0.5278，-0.0553，-0.6948，-0.0971，-0.4196，0.6480，-0.8516，0.4530}

在本次调查问卷范围内，即学校范围内，影响该范围的学生学习状态指标的重要程度可以从上表通过对权重进行排序得出。关注学生的教师可以参考本状态指标，有针对性的对学生进行管理，从而达到提高学生学习自主性，提高学习效果的目的。

四、结语

本文利用BP神经网络原理建立的数学模型具有极好的鲁棒性，是一个能够全面服务于各地域、各年级不同条件的被调查者群体。尤其是对教学一线的教师，让教师有效理解学生学习状态，从而更有效的利用各种教育方法，发挥各种教育理念的最优效果，提高学生学习效果。

[1]Bergmann J，Sams A.Flip your classroom：Reach every student in every class every day[M].Arlington，VA：International Society for Technology in Education，2012.

[2]蒋连香.多元化教学评价指标及评价方法探析.新课程研究，2014，(02).

[3]刘艳春，杨德辉，刘艳丽，康建军.基于神经网络的某型飞机发动机故障诊断研究.电子设计工程，2012，(06).

[4]田雨波.混合神经网络技术.科学出版社，2009，6.

[5]何树红，吴迪，张月秋.比较BP神经网络和RBF神经网络在基金净值预测中的应用.云南民族大学学报，2014，(02).