一道解三角形求最值问题的解法探究
2016-02-25 08:02渠怀莲
中学数学研究(江西) 2016年1期
一道解三角形求最值问题的解法探究
江苏省海门市海门中学(226100)渠怀莲
解三角形历来是高考的热点,而求最值问题尤为重要.这类问题一方面要注重通性通法,另一方面更要注重问题的变式演练.通过改变题目背景、条件、结论等,进行变式演练;追寻问题本源、优化题目的原始解答;探究题目的多种解法,力争多角度审视总结问题,将各知识点串成网络,进而提高学生分析和解决问题的能力.此题目的层层递进设问,培养学生的逻辑思维能力,数学素养,数学潜能,反映了新课标的教学理念.
1.问题本源

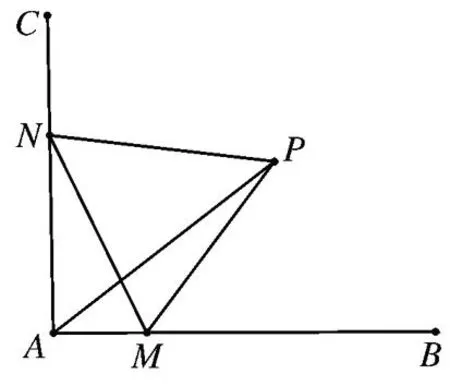
图1
2.设问递进
设∠ANM=θ,当角θ取何值时,线段AP的长取到最大值.
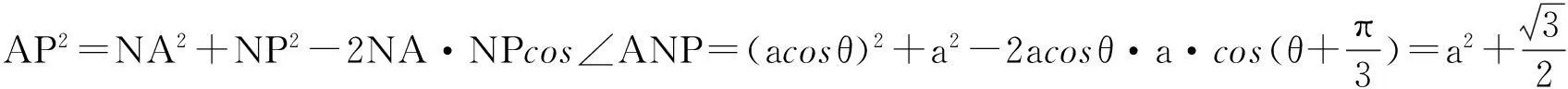

此时,可以让学生思考其它解法进行演练.
3.变式演练

图2
∠AMN=θ,当角θ取何值时,线段AP的长最大.
解法一:“化角”利用三角函数求最值.
设∠AMN=θ,在

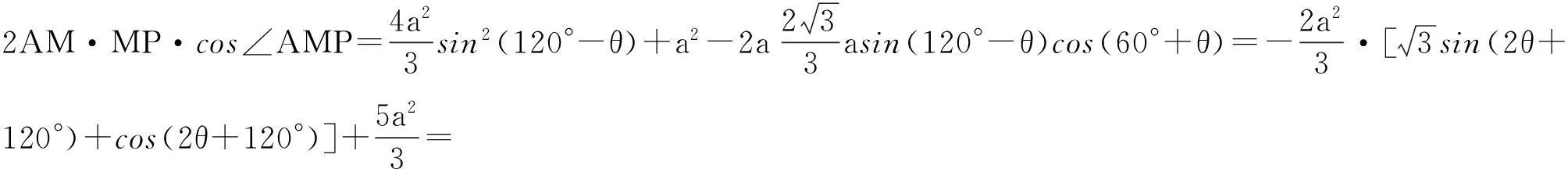

解法二:“化边”利用均值不等式求最值.


4.解法拓展
解法三:“化归”借助坐标变换求最值.

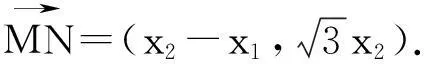



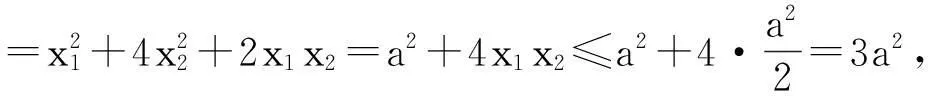
解法四:“画图”利用几何图形性质求最值.
由运动的相对性,可使△PMN不动,点A在运动.

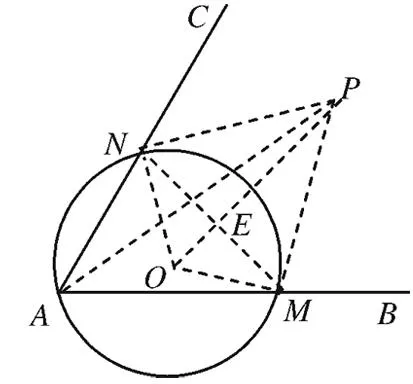
图3

猜你喜欢
中学生数理化(高中版.高二数学)(2022年3期)2022-04-26
中学生数理化(高中版.高考数学)(2021年12期)2021-03-08
中学生数理化·七年级数学人教版(2020年12期)2021-01-18
河北理科教学研究(2020年3期)2021-01-04
中学生数理化(高中版.高二数学)(2020年11期)2020-12-15
中学生数理化(高中版.高考数学)(2020年10期)2020-10-27
中国外汇(2019年6期)2019-07-13
中学数学杂志(2019年1期)2019-04-03
中学生数理化·七年级数学人教版(2018年11期)2019-01-31
中学生数理化·七年级数学人教版(2017年3期)2018-01-20

